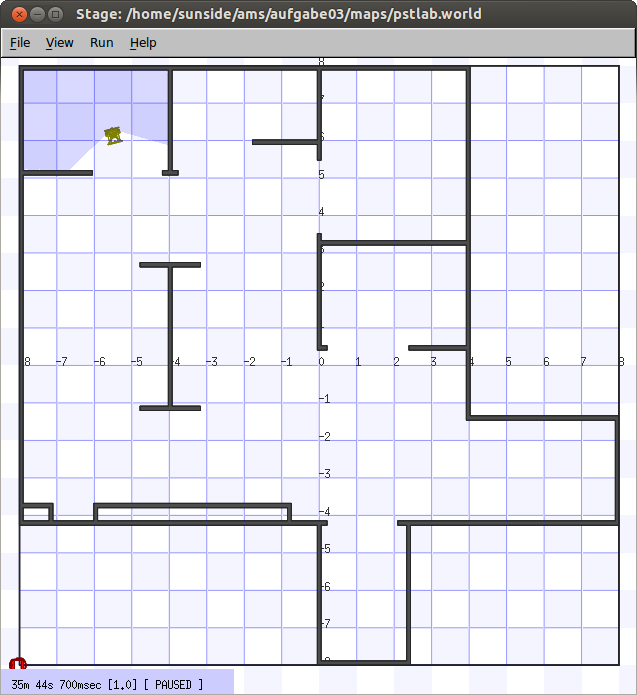
AMS exploration with Player/Stage

A homework solution for the Autonomous Mobile Systems class at Beuth Hochschule für Technik, Berlin with Prof. Dr. Volker Sommer. Runs a simulation of a VolksBot with (error-free) laser rangers.

How to compile the code

To compile and run the code, the following requirements must be fulfilled:

OpenCV (libopencv-dev)
OpenCV highgui (libopencv-highgui-dev)
Player ~ 3.0.2
Stage ~ 4.0.0

The easiest way to compile and start the code is to use Vagrant. After installing, simply run

$ vagrant up

in the project directory to bootstrap a virtual machine that is preconfigured with Player/Stage. The VM will be downloaded if it doesn't already exist your local machine (which is likely if you run the command the first time).

Next, connect to the VM using:

$ vagrant ssh

To build the project, do the following:

$ cd /vagrant
$ make

To power down the VM, issue:

$ vagrant halt

You can then vagrant up it again later. To permanently remove it, type:

$ vagrant destroy
$ vagrant box remove sunside/playerstage

which will delete the VM, as well as the base image.

How to run the code

To run the code, you basically

start player pstlab.cfg
then start ./simple localhost

Note that player and ./simple both require an X11 display. On Linux, you may try passing your $DISPLAY environment when connecting via ssh. The easiest way is to connect to a terminal with X forwarding enabled, using

vagrant ssh -- -X xterm

and then, within the VM, type

cd /vagrant
make
player pstlab.cfg &
./simple localhost

Integrated VNC with browser frontend

For convenience, a dummy Xorg with fluxbox, as well as a noVNC server is started when the VM boots up. In your browser, you may go to http://localhost:6080/vnc.html to connect. Leave the password box empty.

Should you close the Xterm window, try right-clicking the desktop.

About the project

Approach to exploration

This implements a simple approach using meshed P controllers for forward and angular velocity in dependance of the distance to the next obstacle.

You can watch a demo video here.

Stage / robot setup

The robot is modeled without slippage and measurement errors and sports a differential drive with v-omega control.

Robot Map window

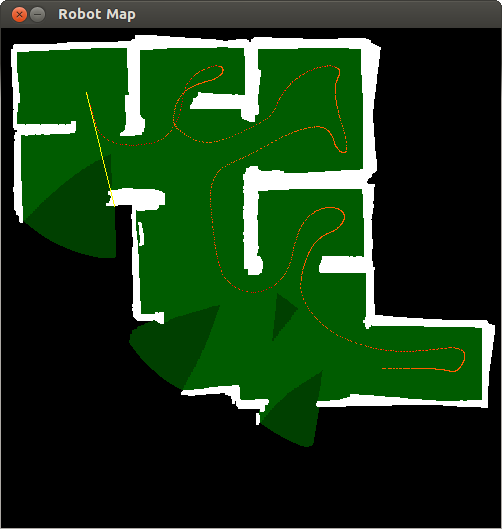
The Robot Map shows the map created by the robot, as well as the past trajectory. The yellow vectors points at the nearest unexplored boundary, using a Manhattan distance measure without paying attention to obstacles. As such, it is measured in air distance, which might be used as a heuristic for A* later on.

Frontiers and algorithm termination

This program implements a frontier-based approach to exploration. A queue-linear flood fill algorithm is used to determine knowledge boundaries (white), i.e. areas that have not been scanned by the robot. The exploration algorithm terminates if no frontiers are left, meaning that the whole terrain has been explored.

More on frontier-based exploration can be found in e.g. A Frontier-Based Approach for Autonomous Exploration by Brian Yamauchi (http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.121.2826)

@INPROCEEDINGS{Yamauchi97afrontier-based,
    author = {Brian Yamauchi},
    title = {A frontier-based approach for autonomous exploration},
    booktitle = {In Proceedings of the IEEE International Symposium on Computational Intelligence, Robotics and Automation},
    year = {1997},
    pages = {146--151}
}

sunsided / bht-ams-playerstage