konimarti / kalman

Adaptive Kalman filter in Golang

Adaptive Kalman filtering in Golang

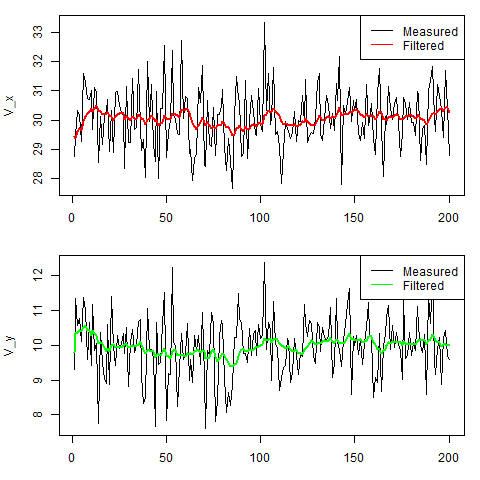
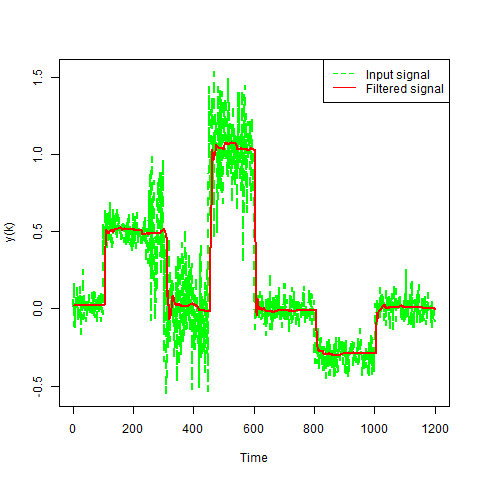
go get github.com/konimarti/kalman

• Adaptive Kalman filtering with Rapid Ongoing Stochastic covariance Estimation (ROSE)

• A helpful introduction to how Kalman filters work, can be found here.

• Kalman filters are based on a state-space representation of linear, time-invariant systems:

  The next state is defined as

  $$x(t+1) = A_d * x(t) + B_d * u(t)$$

  where A_d is the discretized prediction matrix and B_d the control matrix. x(t) is the current state and u(t) the external input. The response (measurement) of the system is y(t):

  $$y(t) = C * x(t) + D * u(t)$$

Using the standard Kalman filter

	// create filter
	filter := kalman.NewFilter(
		lti.Discrete{
			Ad, // prediction matrix (n x n)
			Bd, // control matrix (n x k)
			C,  // measurement matrix (l x n)
			D,  // measurement matrix (l x k)
		},
		kalman.Noise{
			Q, // process model covariance matrix (n x n)
			R, // measurement errors (l x l)
		},
	)

	// create context
	ctx := kalman.Context{
		X, // initial state (n x 1)
		P, // initial process covariance (n x n)
	}

	// get measurement (l x 1) and control (k x 1) vectors
	..

	// apply filter
	filteredMeasurement := filter.Apply(&ctx, measurement, control)
}

Results with standard Kalman filter

See example here.

Results with Rapid Ongoing Stochasic covariance Estimation (ROSE) filter

See example here.

Math behind the Kalman filter

• Calculation of the Kalman gain and the correction of the state vector ~x(k) and covariance matrix ~P(k): $$^y(k) = C * ^x(k) + D * u(k) dy(k) = y(k) - ^y(k) K(k) = ^P(k) * C^T * ( C * ^P(k) * C^T + R(k) )^(-1) ~x(k) = ^x(k) + K(k) * dy(k) ~P(k) = ( I - K(k) * C) * ^P(k)$$
• Then the next step is predicted for the state ^x(k+1) and the covariance ^P(k+1): $$^x(k+1) = Ad * ~x(k) + Bd * u(k) ^P(k+1) = Ad * ~P(k) * Ad^T + Gd * Q(k) * Gd^T$$

Credits

This software package has been developed for and is in production at Kalkfabrik Netstal.