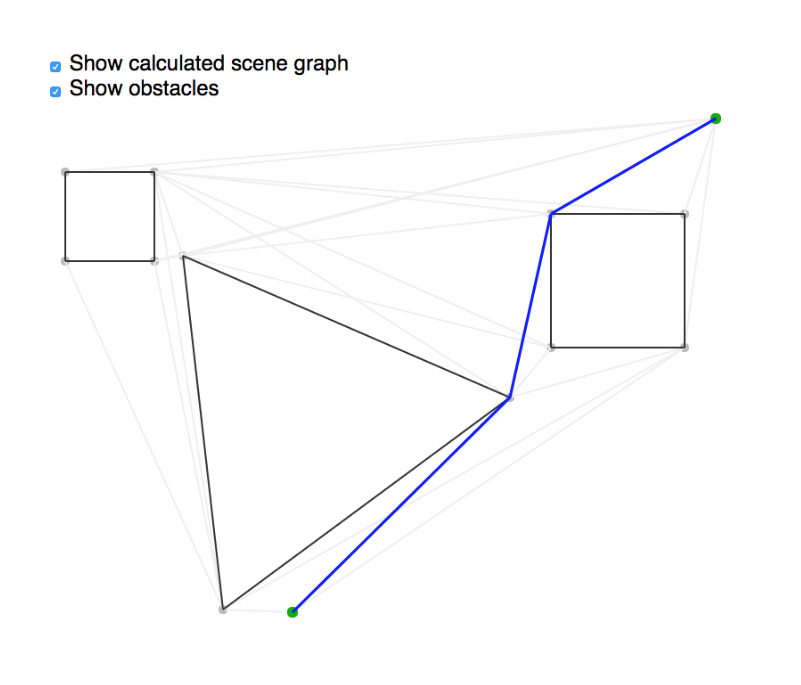
Shortest pathfinding within continuous geometry
Most pathfinding solutions I looked at seemed to be aimed at navigation in one of these two common scenarios:
- Discrete space (i.e. uniformly sized adjacent squares, orthogonal cells, pixels etc). Poor resolution.
- Where a graph of the scene already existed, e.g. a road network as used by satnavs.
I wanted the ability to throw a start point, end point and a list of arbitrary 2d objects with cartesian coordinates at a function and have it return the shortest path through.
To make this happen, graffic first extracts a valid scene graph from the supplied, arbitrary geometry by enumerating nodes and performing point-to-point visibility tests O(N²÷2). With a graph, we can then apply Dijkstra's algorithm to calculate the shortest route.
This is just a fun academic exercise after becoming interested in optimal routes, pathfinding and traffic navigation when walking around the very busy streets of my city.
- Enhanced Dijkstra (minheap), look-ahead, or A*
- BBOX start -> end selection of scene geometry to minimise vis tests
- Spatial indexing (BSP tree? R-tree)
- Only rebuild the parts of the graph that have changed/moved etc