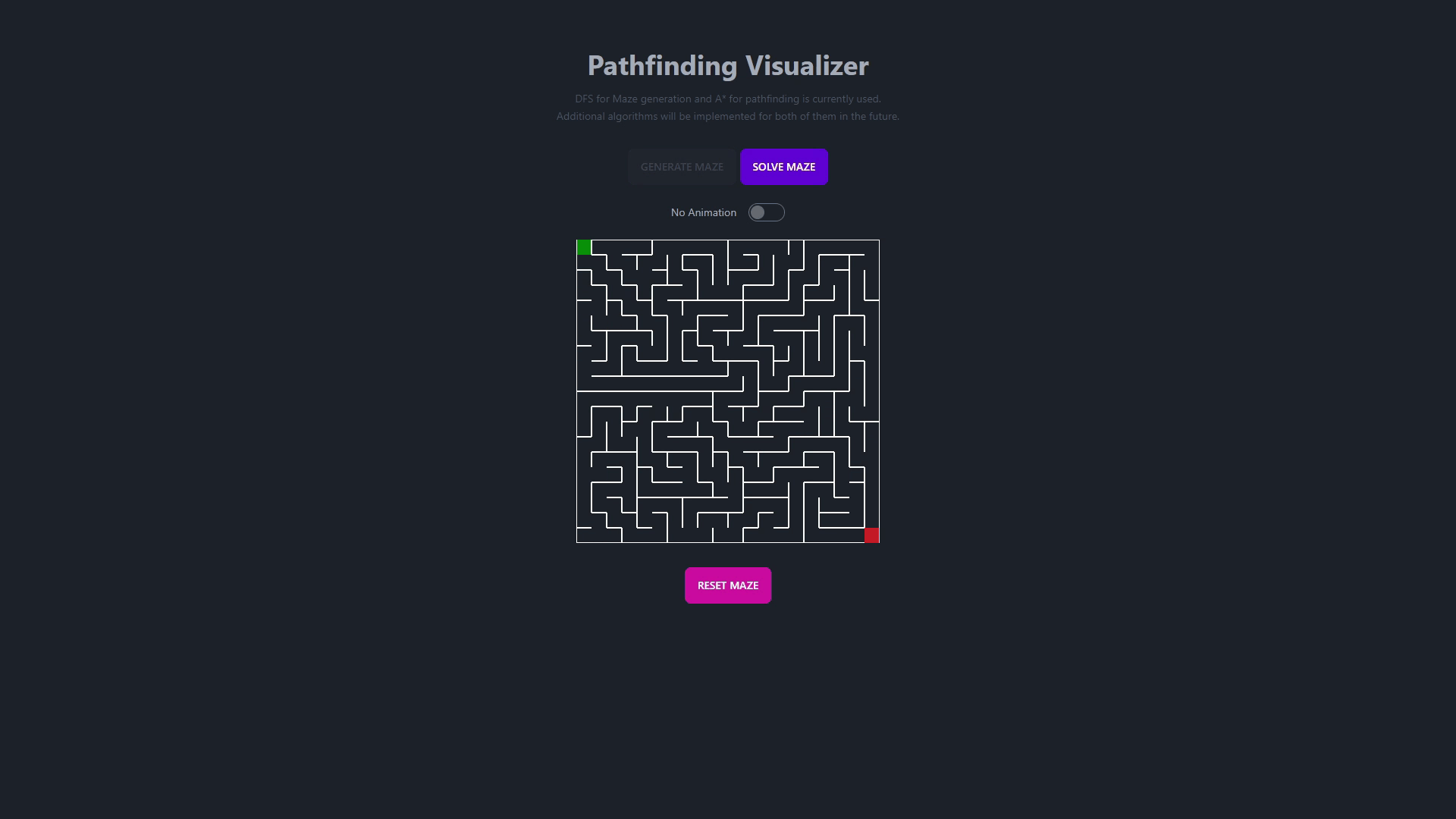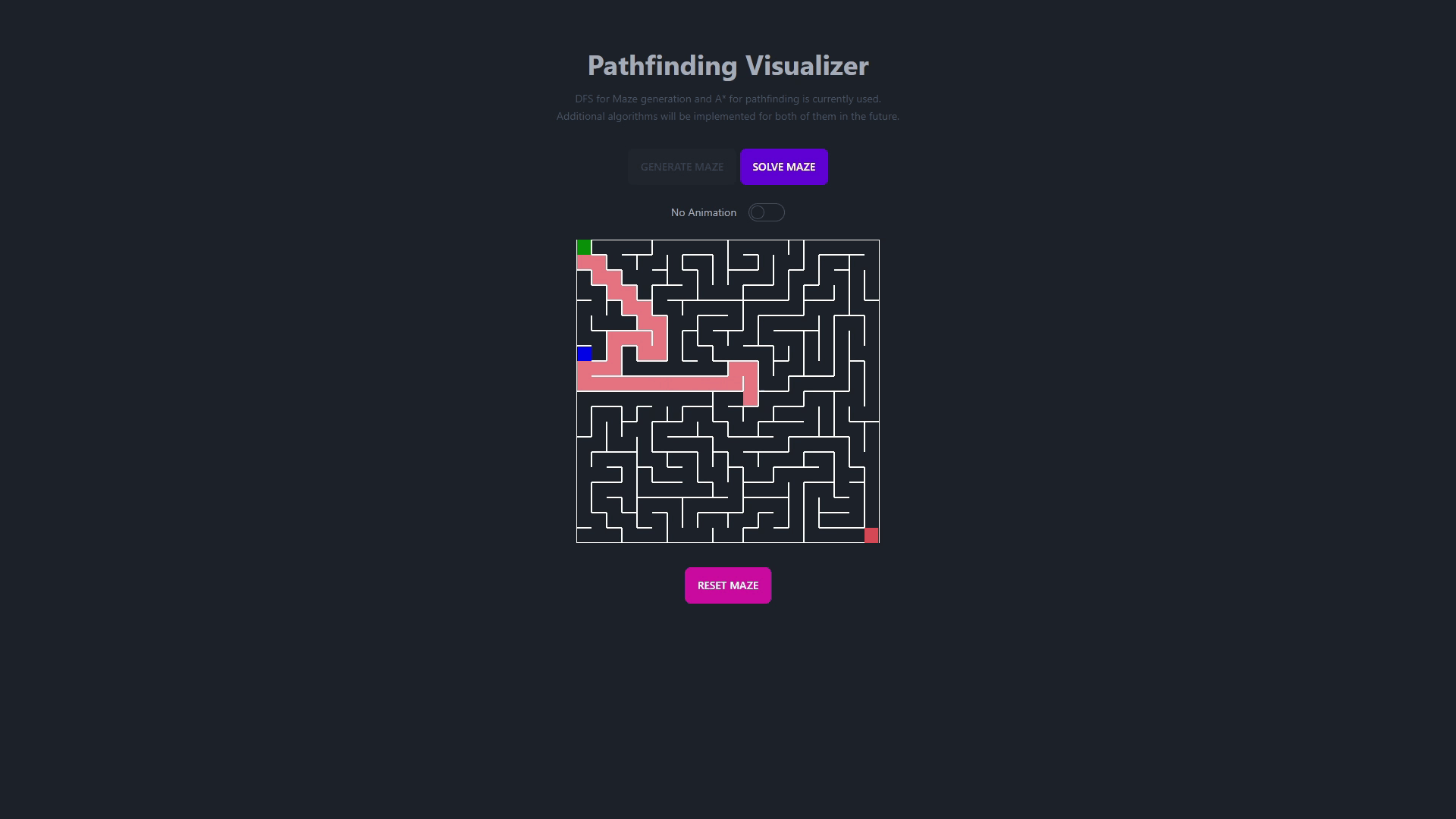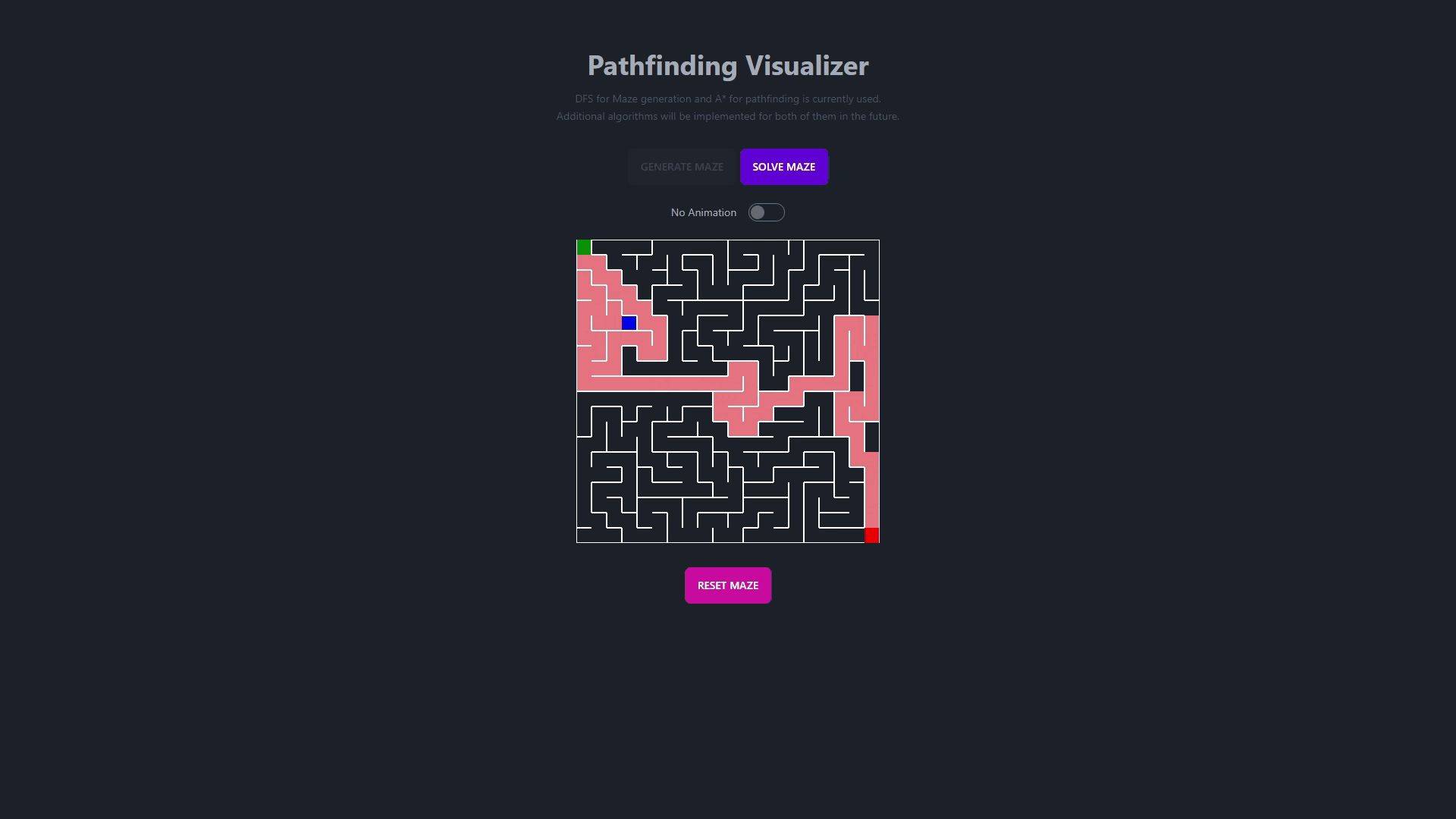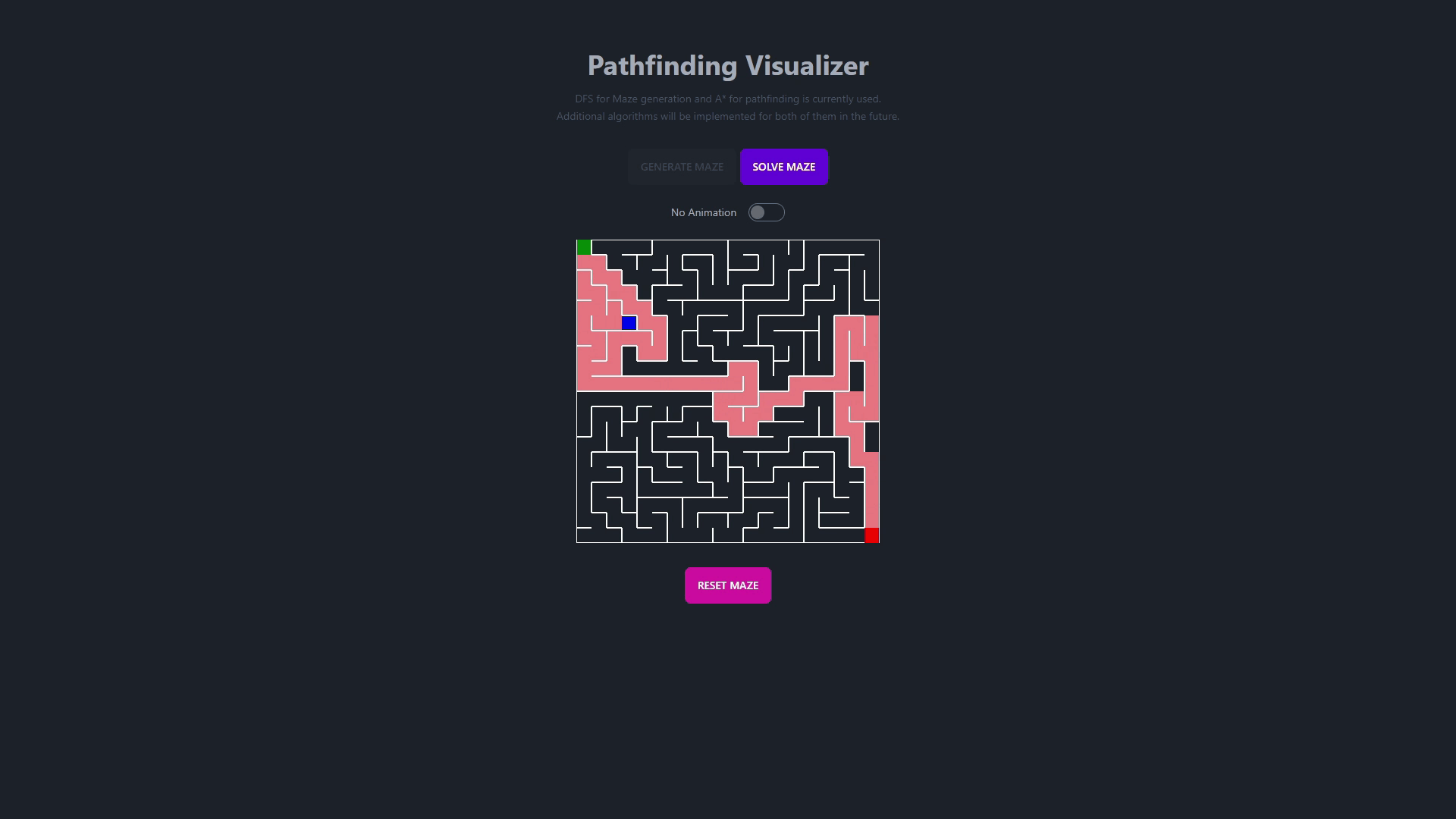
This repository contains a dynamic and interactive visualizer for a wide array of algorithms and data structures. It's designed to provide a clear and educational insight into how different algorithms and data structures work under the hood.
- Sorting Algorithms
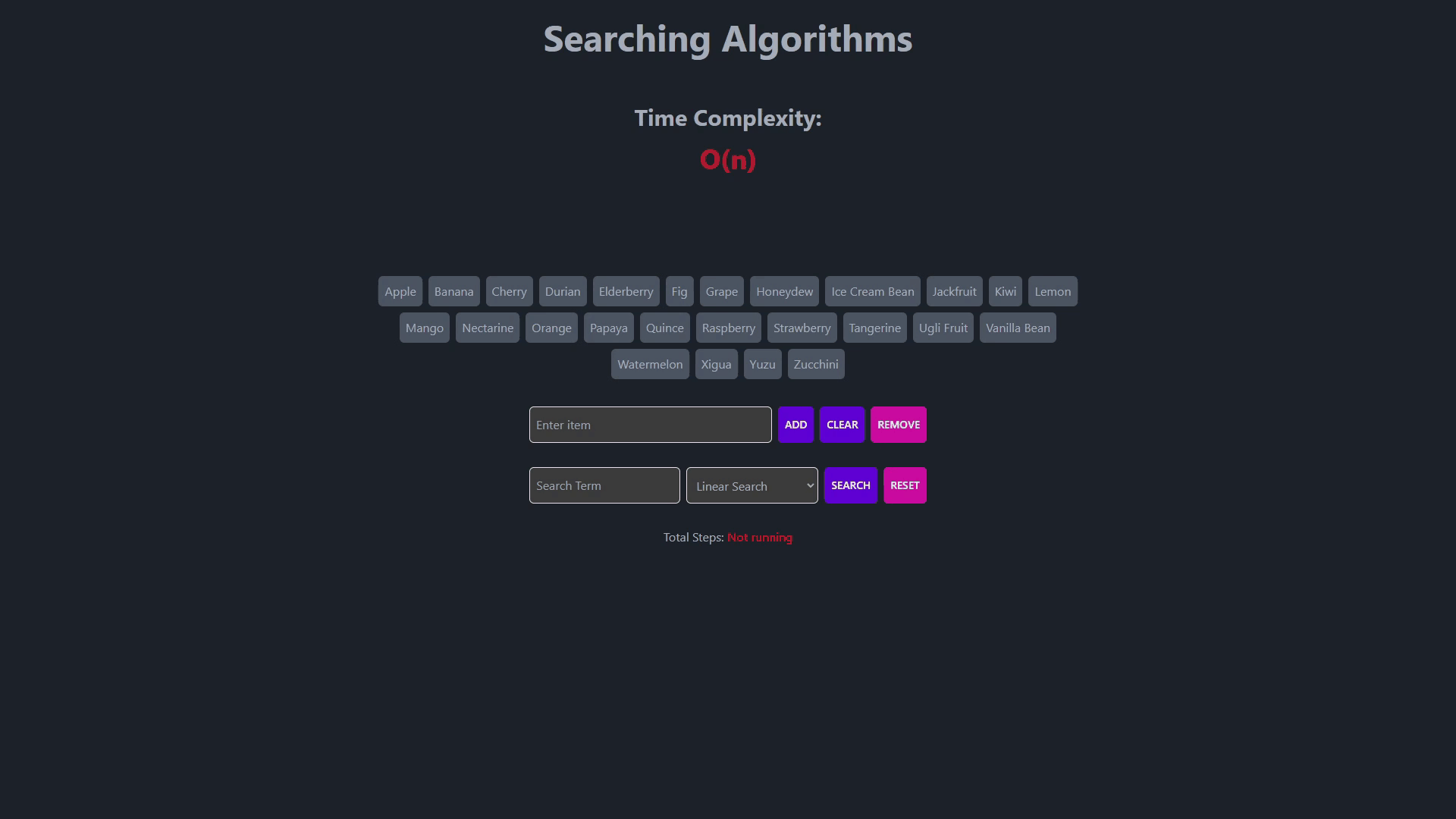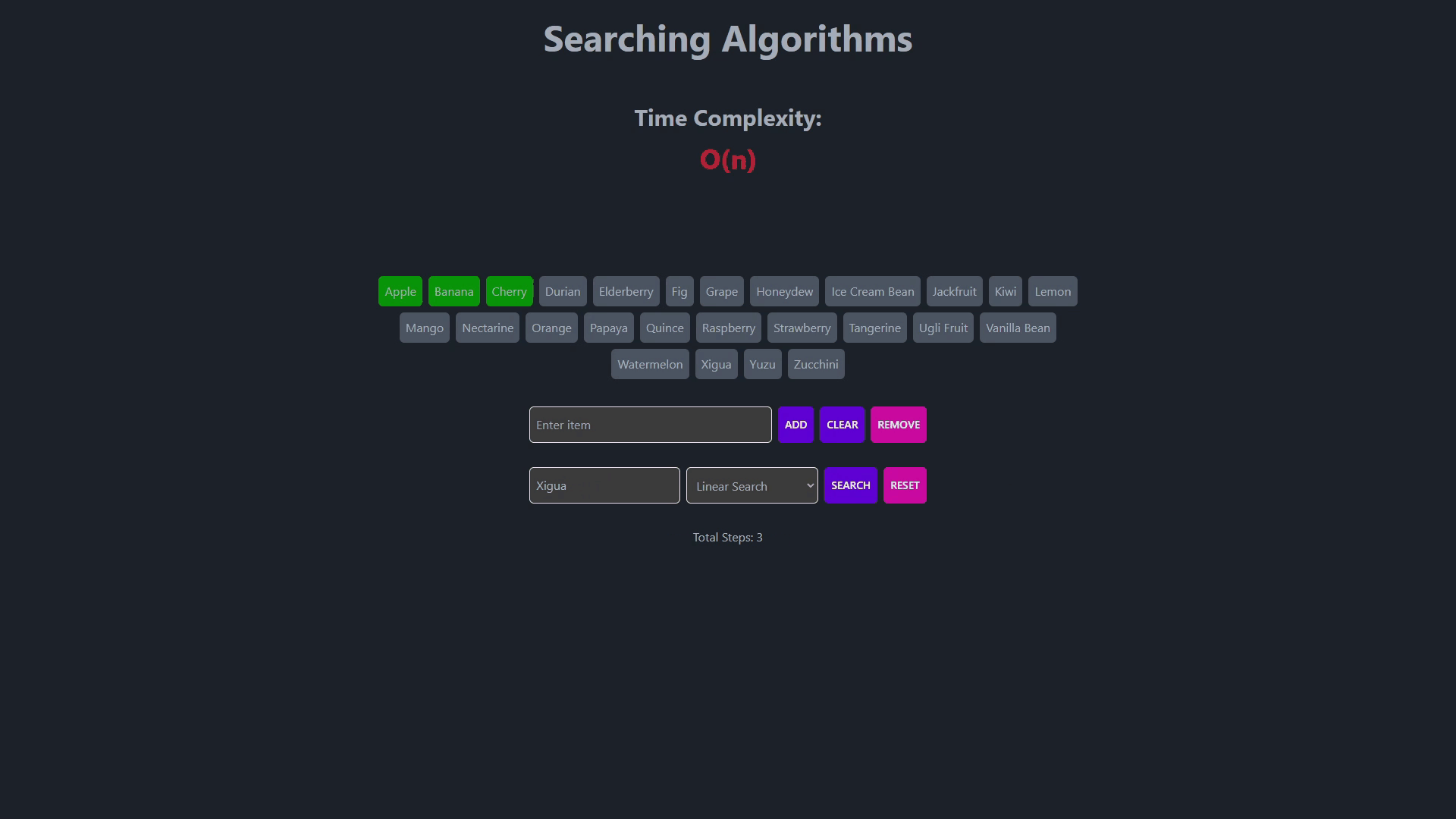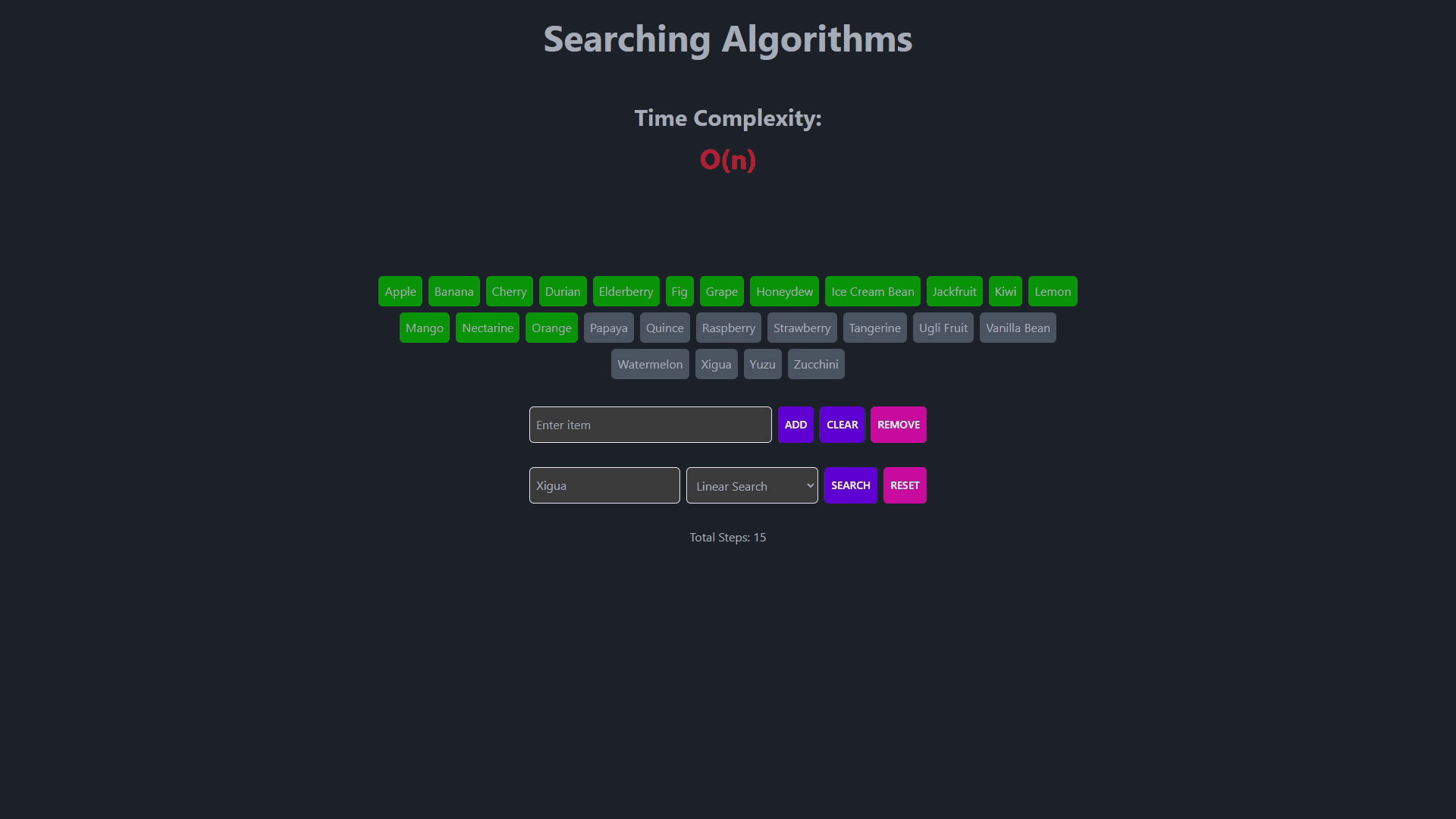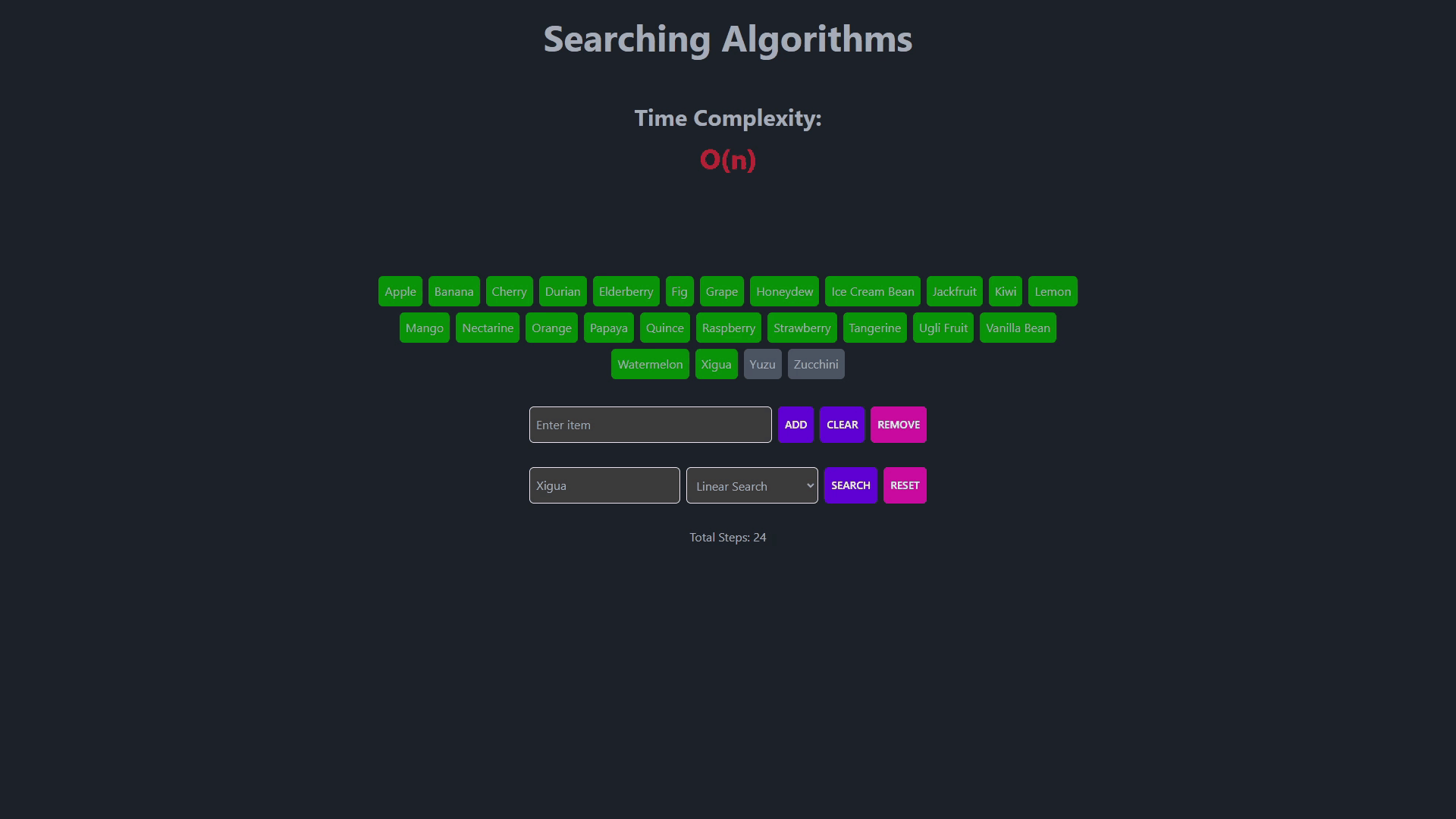
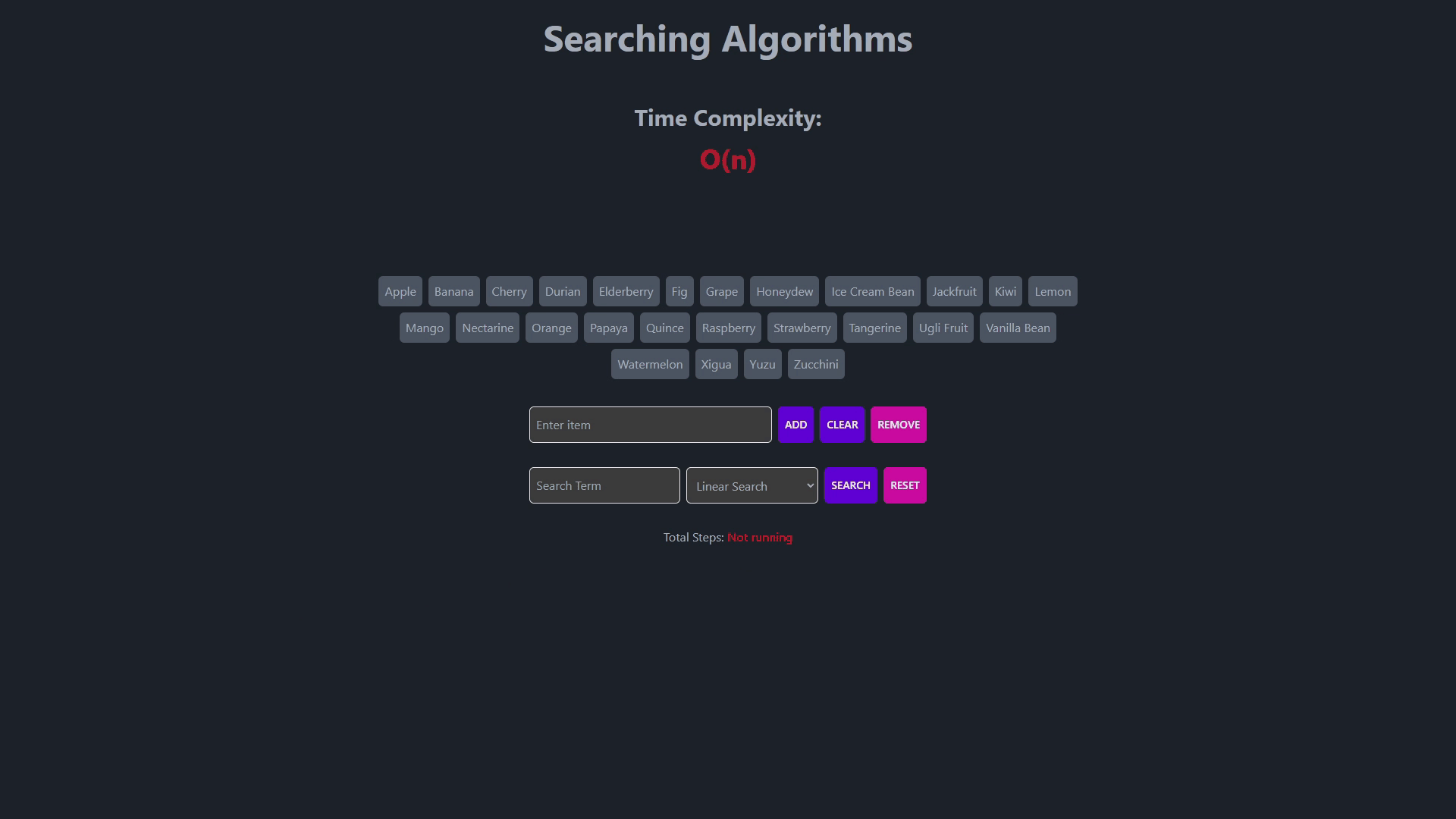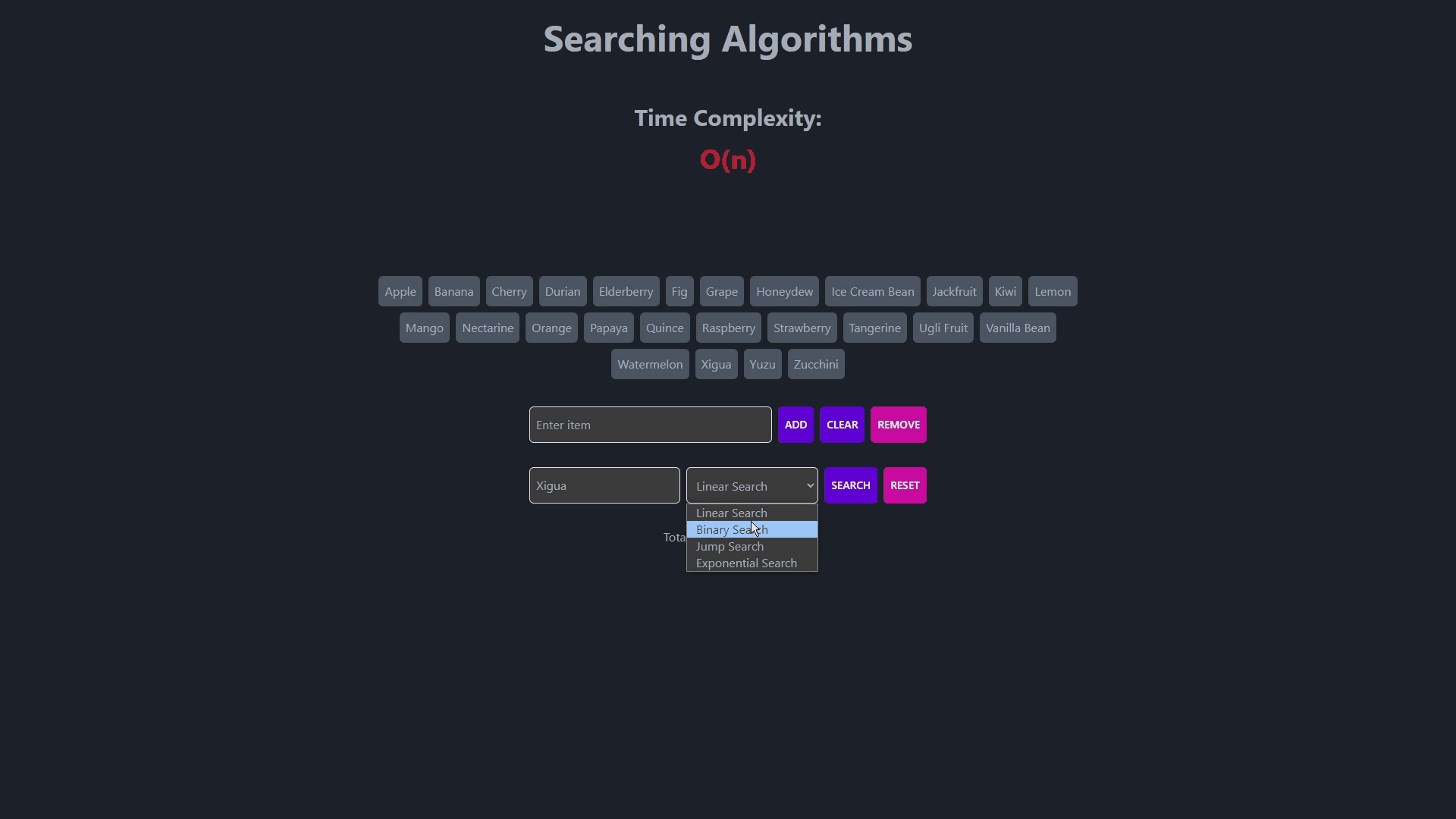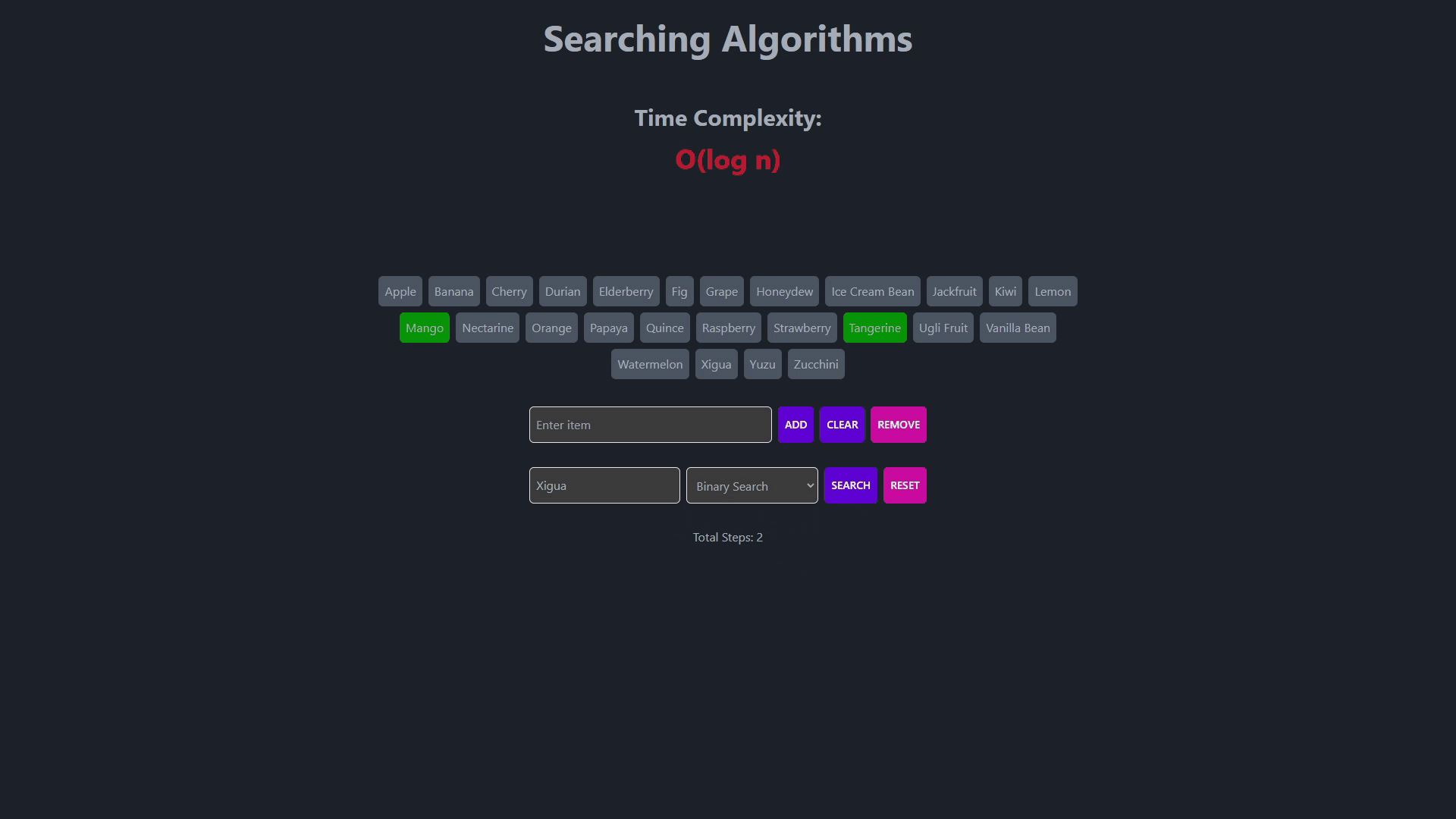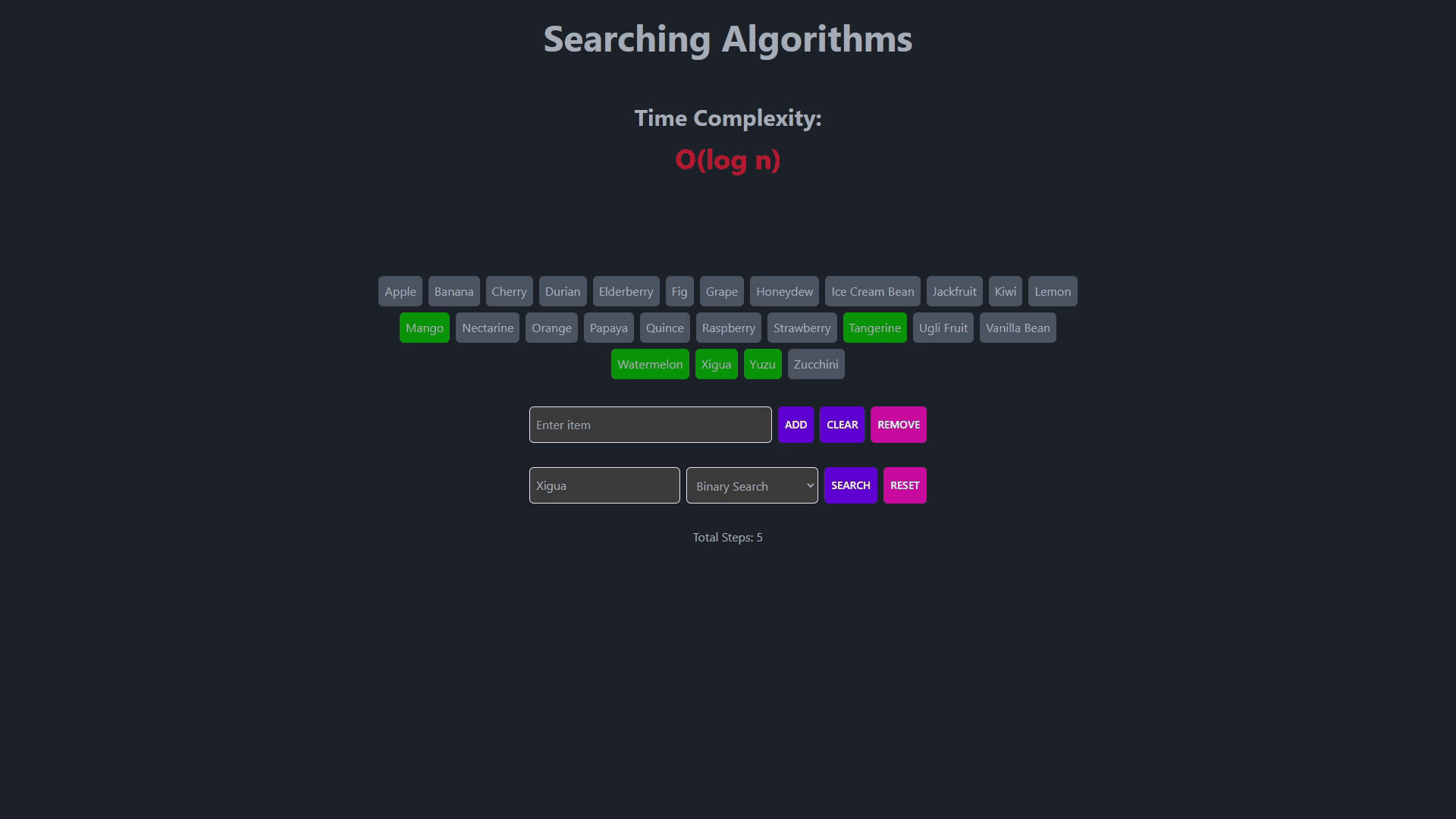
- Searching Algorithms
- Maze Generation Algorithms
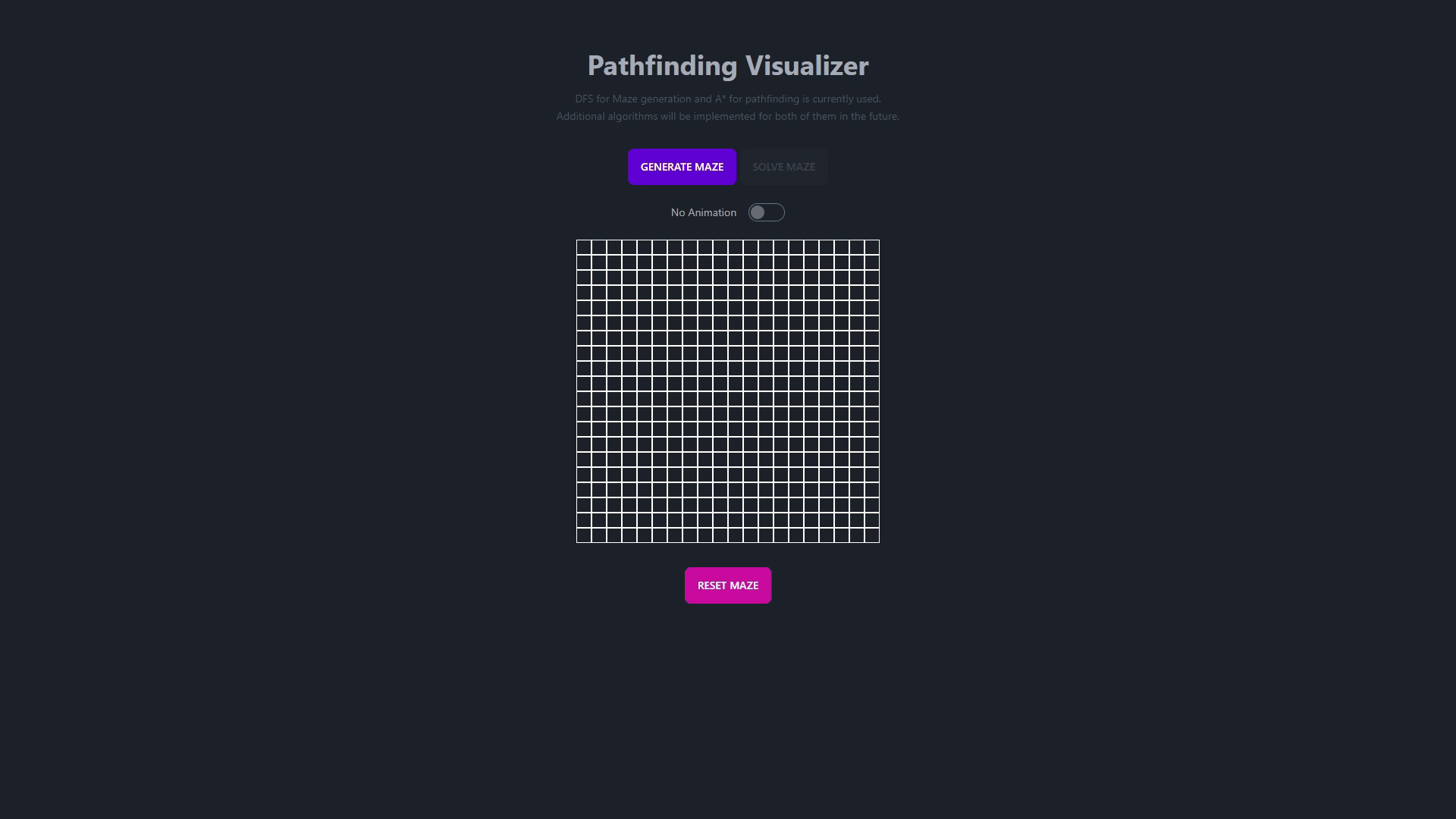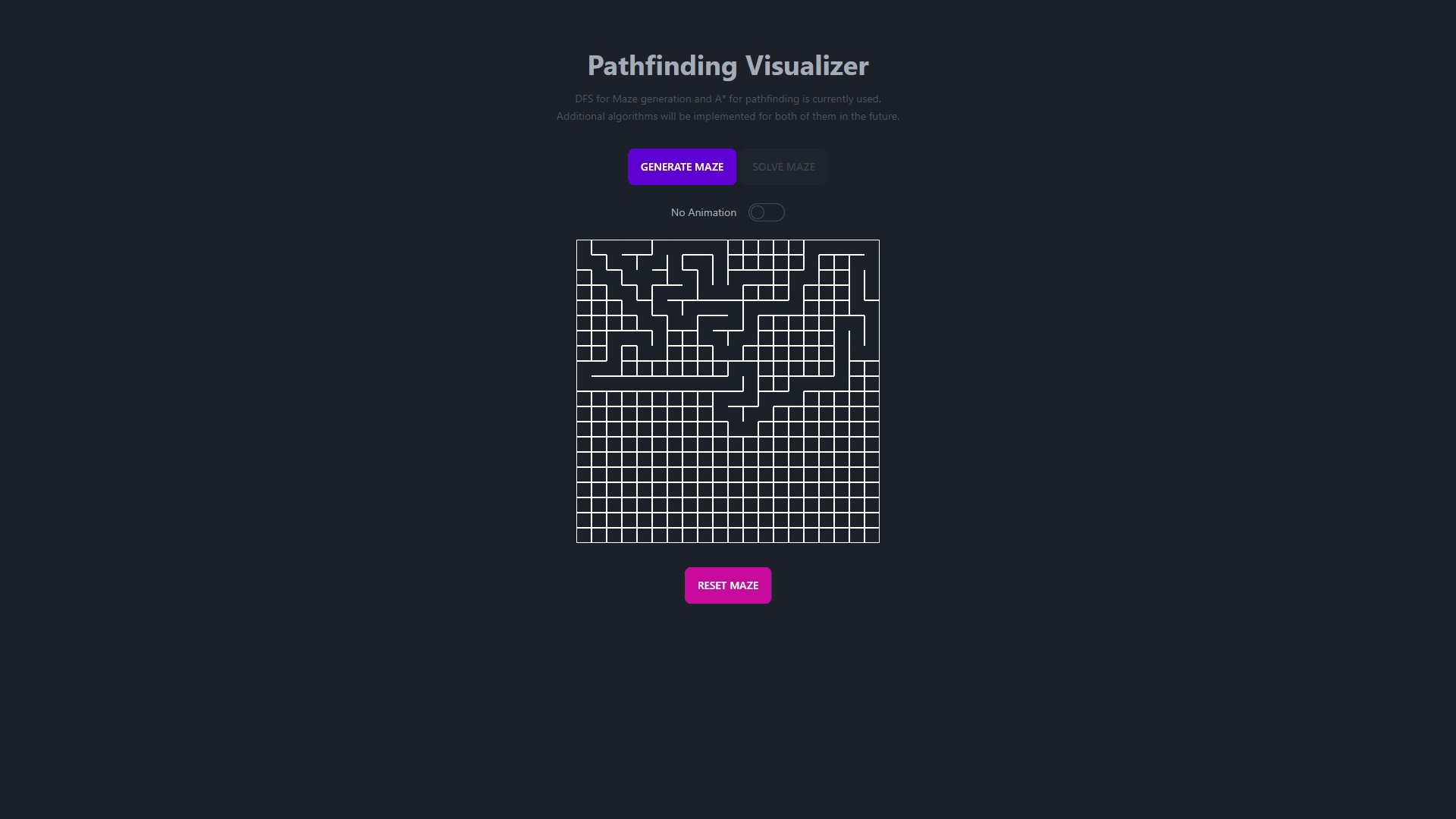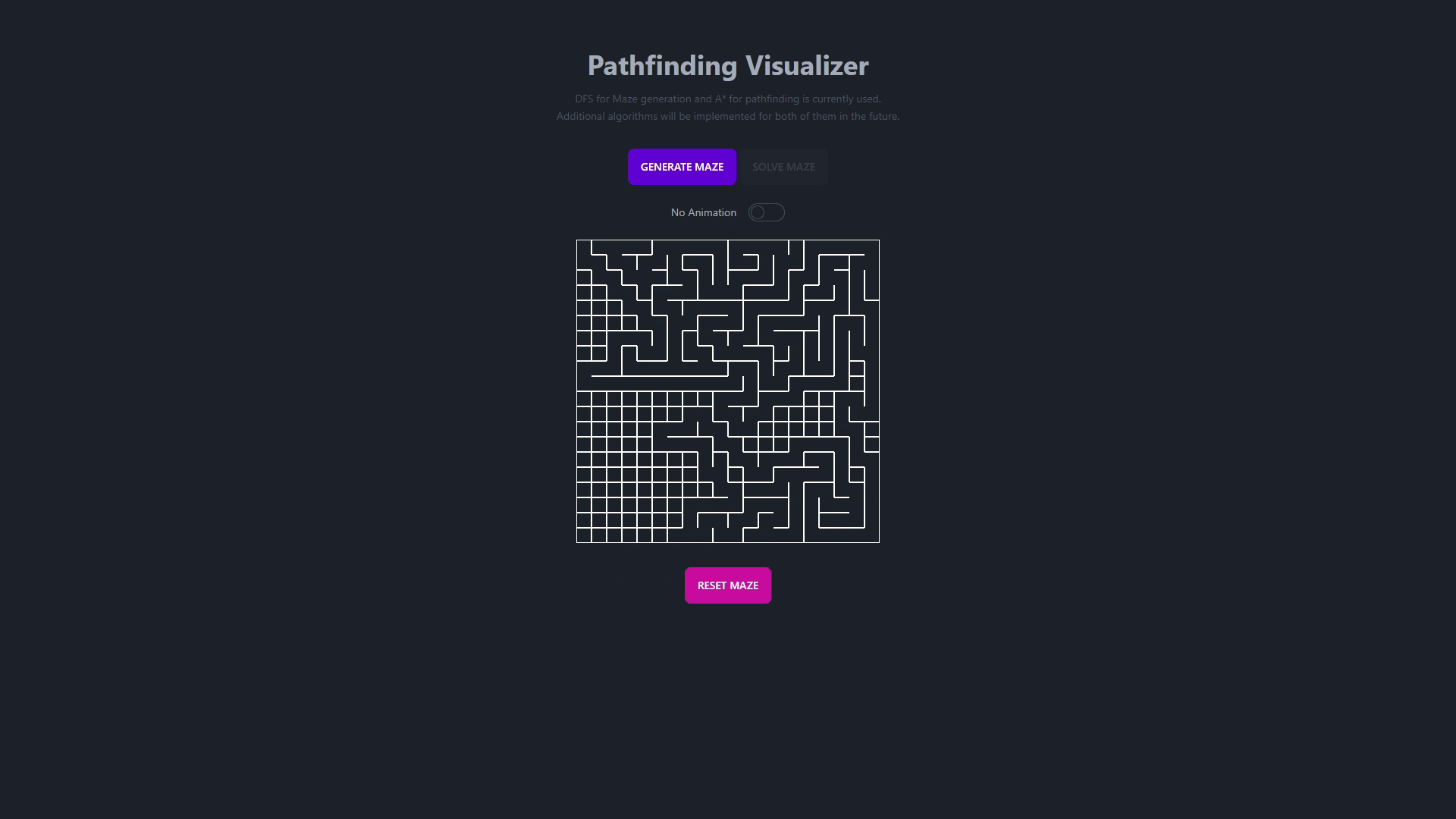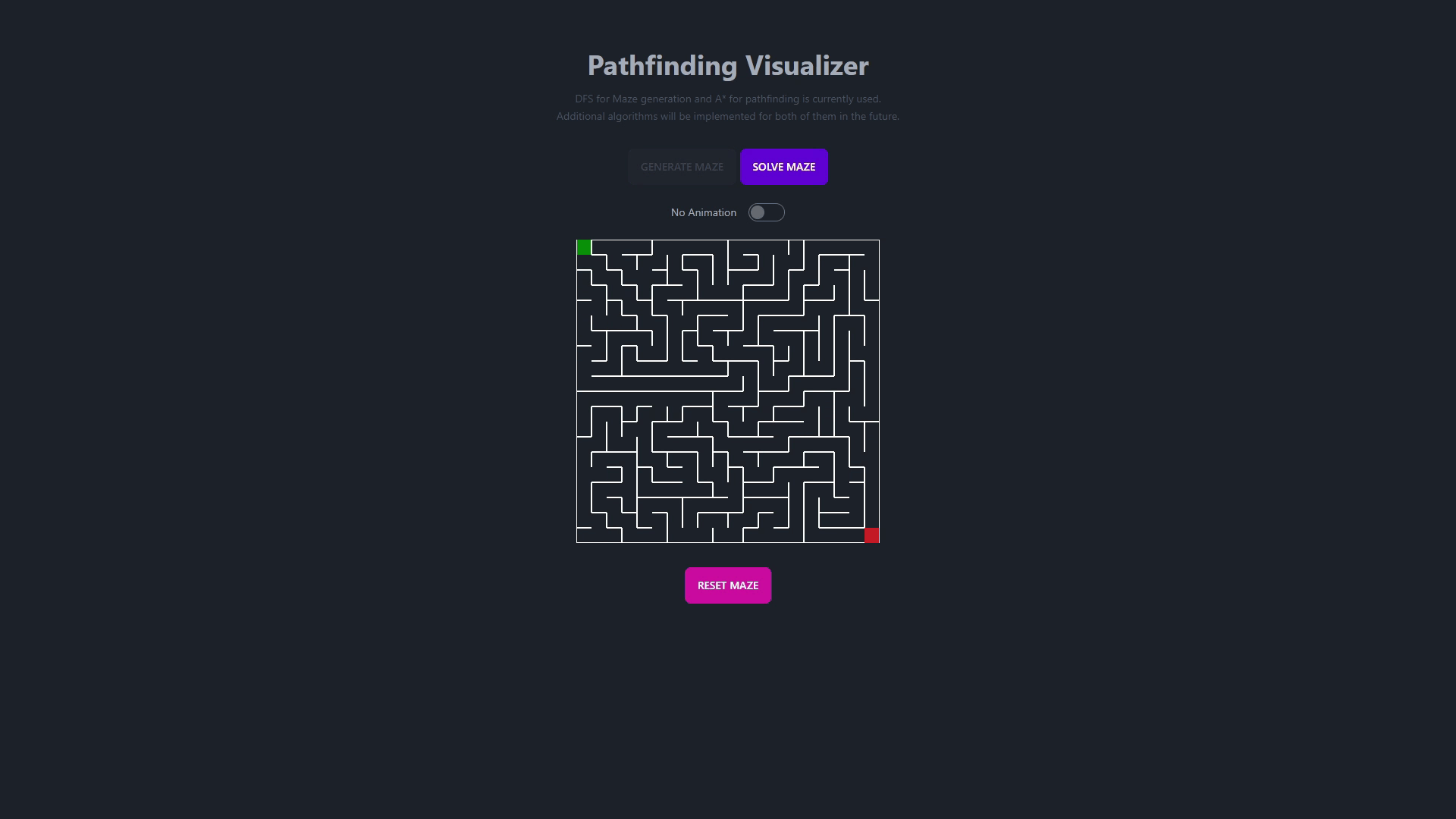
- Pathfinding Algorithms
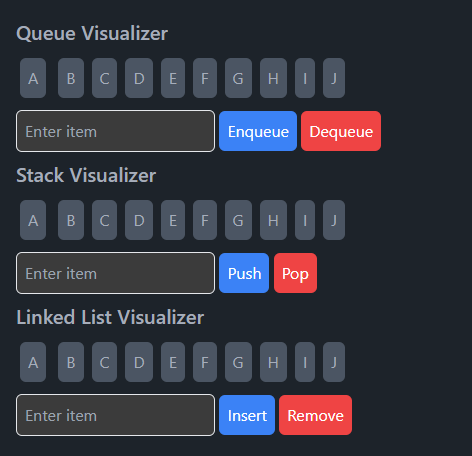
- Data Structures
- Recommendation System
Mergesort and Quicksort have some minor issues with the visualization. I will fix them soon.
- This is the simplest sorting algorithm.
- It repeatedly compares adjacent elements and swaps them if they are in the wrong order.
- Time complexity is O(n2) in the worst case.
- Space complexity is O(1) in the worst case..
- This algorithm sorts an array by repeatedly finding the minimum element from the unsorted part and putting it at the beginning.
- Time complexity is O(n2) in the worst case.
- Space complexity is O(1) in the worst case.
- This algorithm sorts an array by repeatedly inserting an element from the unsorted part into its correct position in the sorted part.
- Time complexity is O(n2) in the worst case.
- Space complexity is O(1) in the worst case.
- This algorithm divides the array into two halves, sorts them separately, and then merges the two sorted halves.
- Time complexity is O(n log n) in the worst case.
- Space complexity is O(n) in the worst case.
- This algorithm picks an element as a pivot and partitions the array around the pivot.
- Time complexity is O(n2) in the worst case.
- Space complexity is O(log n) in the worst case.
- This is the simplest search algorithm.
- It sequentially checks each element in a list until a match is found.
- Works well for small lists or unsorted data.
- Time complexity is O(n) in the worst case.
- This is a more efficient search algorithm, but it requires sorted data.
- It repeatedly divides the search interval in half to find the desired item.
- Time complexity is O(log n) in the worst case.
- Jump Search divides the list into smaller blocks and checks these blocks to reduce the number of comparisons.
- Requires sorted data.
- Time complexity is O(√n) in the worst case.
- Exponential Search finds the range in which the desired item is located by jumping 2i elements in every iteration and then performs a binary search in that range.
- Requires sorted data.
- Time complexity is O(log n) in the worst case.
- Complexity: Simplest
- This algorithm creates a maze by repeatedly carving passages either to the north or to the east.
- It is a simple algorithm, but it produces mazes with a strong north-east bias.
- It doesn't require maintaining a complex state or backtracking.
- Complexity: Moderate
- Involves a stack and backtracking to create a maze
- It generates mazes with a single solution and a moderate level of complexity, but the paths tend to have a long and winding nature.
- Complexity: More Complex
- This algorithm creates a maze by randomly selecting a wall from the list of walls that separate cells in the maze and removing it if the cells on both sides of the wall belong to different sets.
- It's more efficient in space utilization than the DFS method.
- Complexity: Most Complex
- This algorithm creates a maze by randomly selecting a wall from the list of walls that separate cells in the maze and removing it if the cells on both sides of the wall belong to different sets.
- Produces mazes with a high degree of complexity and less bias compared to the other algorithms.
- Complexity: A little more complex than DFS
- This algorithm creates a maze by randomly selecting a cell and carving a passage in a random direction from that cell.
- It then performs a random walk, carving passages to unvisited cells until it reaches a dead end.
- This algorithm finds the shortest path between two nodes in a graph.
- It uses a priority queue to keep track of the next node to visit.
- This algorithm is an extension of Dijkstra's algorithm.
- It uses a heuristic function to estimate the distance between the current node and the destination node.
- It uses a priority queue to keep track of the next node to visit.
- It is faster than Dijkstra's algorithm.
- This algorithm finds the shortest path between two nodes in a graph.
- It uses a queue to keep track of the next node to visit.
- This algorithm finds the shortest path between two nodes in a graph.
- It uses a stack to keep track of the next node to visit.
- A stack is a linear data structure that follows the Last In First Out (LIFO) principle.
- It has two main operations: push and pop.
- It can be implemented using an array or a linked list.
- Time complexity of push and pop operations is O(1).
- Space complexity is O(n).
- A queue is a linear data structure that follows the First In First Out (FIFO) principle.
- It has two main operations: enqueue and dequeue.
- It can be implemented using an array or a linked list.
- Time complexity of enqueue and dequeue operations is O(1).
- Space complexity is O(n).
- A linked list is a linear data structure that consists of nodes.
- Each node has a data field and a pointer to the next node.
- It can be implemented using a singly linked list or a doubly linked list.
- Time complexity of insertion and deletion operations is O(1).
- Space complexity is O(n).
Will not be implemented
- This algorithm finds similar users based on their ratings and recommends items that they have rated highly.
- It uses the Pearson correlation coefficient to measure the similarity between users.
- It uses the weighted average of ratings to predict the ratings of items.
- This algorithm recommends items that are similar to the items that the user has liked in the past.
- It uses the cosine similarity to measure the similarity between items.
- It uses the weighted average of ratings to predict the ratings of items.
- Get images from unsplash
- Use GCP Vision API to get labels
{
"1.jpg": [
{
"locations": [],
"properties": [],
"mid": "/m/0c9ph5",
"locale": "",
"description": "Flower",
"score": 0.9955990314483643,
"confidence": 0,
"topicality": 0.9955990314483643,
"boundingPoly": null
},
{
"locations": [],
"properties": [],
"mid": "/m/04sjm",
"locale": "",
"description": "Flowering plant",
"score": 0.9854584336280823,
"confidence": 0,
"topicality": 0.9854584336280823,
"boundingPoly": null
},
[...]
]
}- Format data
- Calculate TF-IDF
- Calculate cosine similarity between images
- Use labels to find similar images
- Use similar images to find similar items
- Use similar items to recommend items