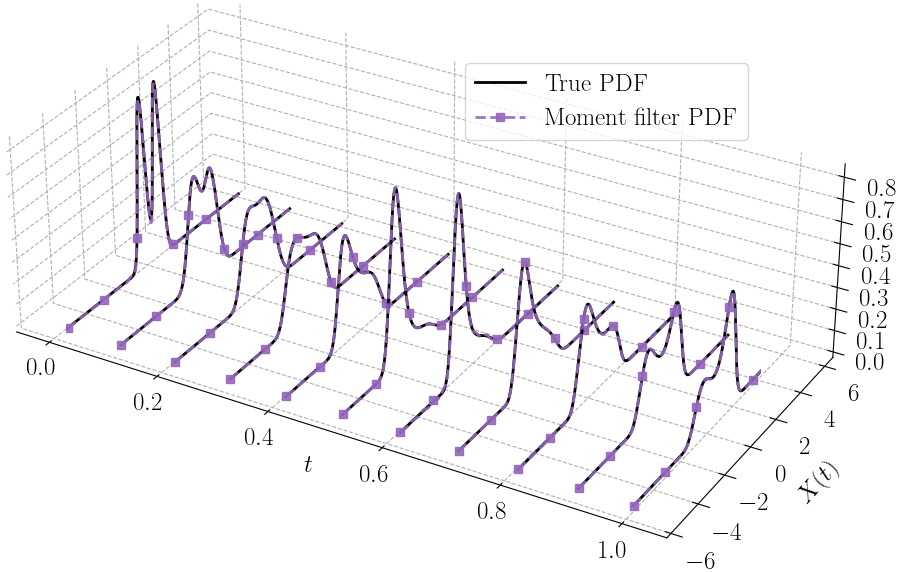
Implementation of the moment filter introduced in the paper "Stochastic filtering with moment representation". Please cite as follows to use the implementation.
@article{
author = {Zheng Zhao and Juha Sarmarvuori},
title = {Stochastic filtering with moment representation},
journal = {arXiv preprint arXiv:2303.13895},
year = {2023},
}Please feel free to find the preprint at https://arxiv.org/abs/2303.13895.
Consider a model
or
for
Under mild system conditions, the filter converges to the true solution in moments and distribution as
The implementation is based on JAX. Depending on your computer platform (e.g., CPU/GPU/TPU), the installation of JAX can be different. Hence, please first refer to this official guidance to install JAX by yourself.
After you have JAX installed, then do
git clone git@github.com:zgbkdlm/mfs.gitorgit clone https://github.com/zgbkdlm/mfs.git.cd mfspip install -r requirements.txtpip install -r testing_requirements.txtpython setup.py installorpython setup.py developfor the editable model. Ifsetup.pyis deprecated, then dopython -m pip install .instead.
You can find a few examples in ./examples to help you use get started with the moment filter.
A sketch of using raw moments for 1D filtering is given as follows.
import jax
from mfs.one_dim.filtering import moment_filter_rms
# Define your model here
def sde_cond_rms(x, n):
"""The transition moment E[X_k^n | X_{k-1} = x].
"""
return ...
def pdf_y_cond_x(y, x):
"""The measurement PDF p(y | x).
"""
return ...
# Your data
ys = ...
# Initial raw moments
rms0 = ...
# JIT moment filter
@jax.jit
def moment_filter(_ys):
return moment_filter_rms(sde_cond_rms, pdf_y_cond_x, rms0, _ys)
# rmss are the filtering raw moments, and nell is the negative log-likelihood
rmss, nell = moment_filter(ys)To exactly reproduce the figures/tables/numbers in the paper, please refer to the instructions in ./reproduce_paper_plots, and also the instructions in ./dardel.
During the development time of this work, I have also experimented a bunch of side-implementations in JAX, which are related/unrelated to this moment filter. I would be glad if you find them useful for your projects:
- A bunch of commonly used filters and smoothers, such as extended Kalman filter, sigma-points filters, and particle filters (
mfs.classical_filters_smoothers). - Brute-force filter (
mfs.classical_filters_smoothers.brute_force). This can handily compute the true filtering solution for 1D state up to machine precision. You can use this as a benchmark to gauge your method. - The Kan--Magnus method for efficiently computing Gaussian moments (
mfs.multi_dims.moments). - Graded lexicographical ordering (
mfs.multi_dims.multi_indices). - Gram--Charlier series (
mfs.one_dim.pdf_approximations). - Saddle point approximation (
mfs.one_dim.pdf_approximations). - Posterior Cramér--Rao lower bound for filtering (
mfs.utils). - Partial and complete Bell polynomials (
mfs.utils). - Legendre polynomial expansion (
mfs.one_dim.pdf_approximations). - Lánczos algorithm (
mfs.utils).
In the coming days, we will upload some demonstrations written in MATLAB and Julia under the folders ./matlab and ./julia, respectively. Please note that these implementations are for proof-of-concept only, and that they do not reproduce the results in the paper.
The GNU General Public License v3 or later. See ./LICENSE.
Zheng Zhao, Uppsala University, firstname.lastname@it.uu.se, https://zz.zabemon.com.
Juha Sarmavuori, Aalto University, firstname.lastname@aalto.fi.