statmlben / nonlinear-causal

nl-causal: nonlinear causal inference based on IV regression in Python

🧬 nonlinear-causal

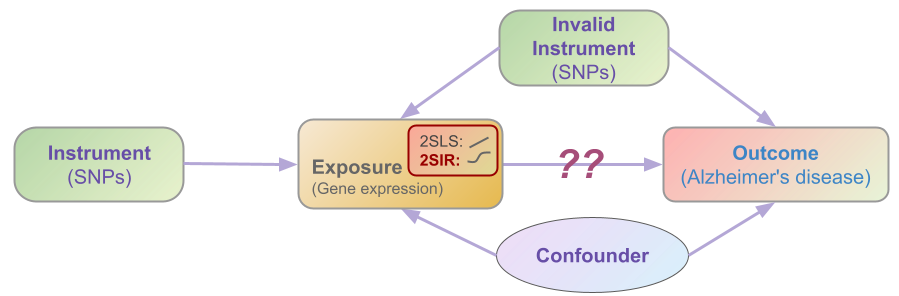
nonlinear-causal is a Python module for nonlinear causal inference, including hypothesis testing and confidence interval for causal effect, built on top of instrument variables and Two-Stage least squares (2SLS).

• GitHub repo: https://github.com/nl-causal/nonlinear-causal
• PyPi: https://pypi.org/project/nonlinear-causal/
• Paper: PMLR@CLeaR2024
• Documentation: https://nonlinear-causal.readthedocs.io

Models

nonlinear-causal considers two instrument variable causal models:

Illustrated by the above image example, let's denote $\mathbf{z}$ as the valid/invalid instrument variables (such as SNPs), $x$ as the exposure (such as gene expression), and $y$ as the outcome (such as AD).

Two-Stage least squares (2SLS)

$$ x = \mathbf{z}^\prime \mathbf{\theta} + w, \quad y = \beta x + \mathbf{z}^\prime \mathbf{\alpha} + \epsilon, $$

where $(w,\varepsilon)$ are the error terms independent of the instruments $\mathbf{z}$, however, $w$ and $\varepsilon$ may be correlated due to underlying confounders, and $\beta\in\mathbb{R}$, $\mathbf{\alpha}\in\mathbb{R}^p$, $\mathbf{\theta}\in\mathbb{R}^p$ are unknown parameters.

Two-Stage Sliced Inverse Regression (2SIR)

$$ \phi(x) = \mathbf{z}^\prime \mathbf{\theta} + w, \quad y = \beta \phi(x) + \mathbf{z}^\prime \mathbf{\alpha} + \epsilon, $$

where $(w,\varepsilon)$ are the error terms independent of the instruments $\mathbf{z}$, however, $w$ and $\varepsilon$ may be correlated due to underlying confounders, and $\beta\in\mathbb{R}$, $\mathbf{\alpha}\in\mathbb{R}^p$, $\mathbf{\theta}\in\mathbb{R}^p$ are unknown parameters.

Remarks

• 2SLS / 2SIR. $\mathbf{\alpha} \neq \mathbf{0}$ indicates the violation of the second and/or third IV assumptions. The models may not be identifiable with the presence of invalid IVs. In the literature, additional structural constraints are imposed to avoid this issue, such as $|\mathbf{\alpha}|_0 < p/2$.
• 2SIR. $\beta$ and $\phi$ are identifiable by fixing $|\mathbf{\theta}|_2 = 1$ and $\beta \geq 0$.

Strengths of 2SIR

• Model assumptions of 2SIR are weaker than the classical 2SLS: the model admits an arbitrary nonlinear transformation $\phi(\cdot)$ across $\mathbf{z}$, $x$ and $y$, relaxing the linearity assumption in the standard TWAS/2SLS.
• 2SIR includes 2SLS and Yeo-Johnson power transformation 2SLS (PT-2SLS) as special cases. It is worth mentioning that the proposed method remains competitive against 2SLS/PT-2SLS even if the linear assumption holds.
• The implicit linear structure in both 2SLS and 2SIR allows the use of GWAS summary data of our method, in contrast to requiring individual-level data by the other (non-linear) models.

What We Can Do:

2SLS

• Estimate $\beta$: marginal causal effect from $X \to Y$
• Hypothesis testing (HT) and confidence interval (CI) for marginal causal effect $\beta$.

2SIR

• Estimate $\beta$: marginal causal effect from $X \to Y$
• Hypothesis testing (HT) and confidence interval (CI) for marginal causal effect $\beta$.
• Estimate nonlinear causal link $\phi(\cdot)$.

For implementation usage of nonlinear_causal, kindly refer to the provided examples and notebooks.

Installation

# Install the latest version `nonlinear-causal` in Github:
pip install git+https://github.com/nl-causal/nonlinear-causal
# or Install `nonlinear-causal` lib from `pypi`
pip install nonlinear-causal

Examples and notebooks

• User guide
• Simulated examples
• Simulated examples with invalid IVs
• Real application

Simulation Performance

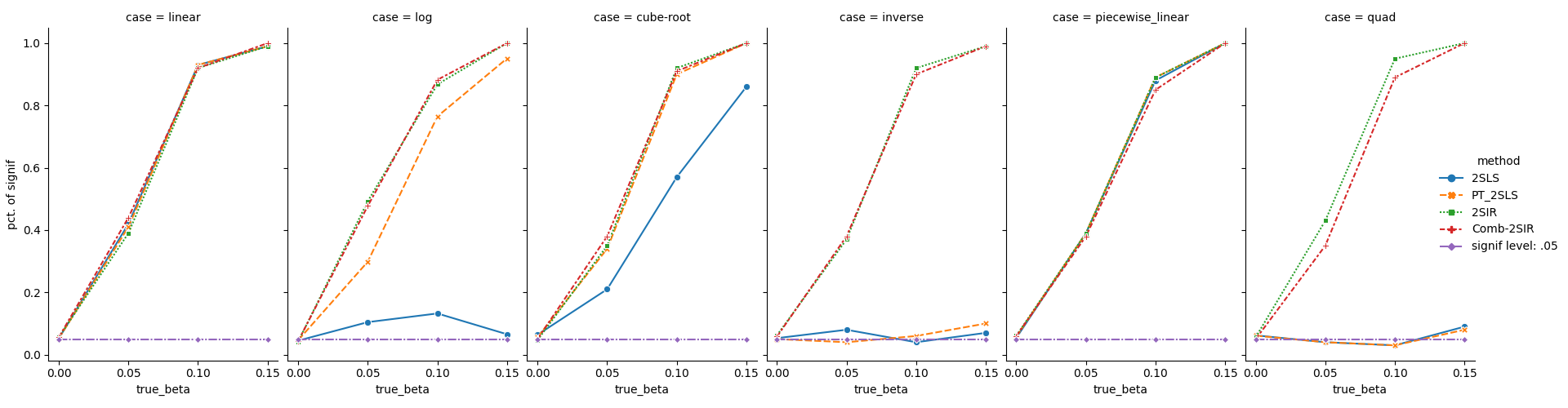
• We examine four cases: (i) $\beta = 0$, (ii) $\beta = .05$, (iii) $\beta = .10$, (iv) $\beta = .15$. Note that case (i) is for Type I error analysis, while $\beta > 0$ in (ii) - (iv), suggests power analysis.

• Six transformations are considered: (1) linear: $\phi(x) = x$; (2) logarithm: $\phi(x) = \log(x)$; (3) cube root: $\phi(x) = x^{1/3}$; (4) inverse: $\phi(x) = 1/x$; (5) piecewise linear: $\phi(x) = xI(x\leq 0) + 0.5 x I(x > 0)$; (6) quadratic: $\phi(x) = x^2$.

For more information, please check our paper (Section 3) or the Jupyer Notebook for the simulation examples.

Reference

If you use this code please star 🌟 the repository and cite the following paper:

• Dai, B., Li, C., Xue, H., Pan, W., & Shen, X. (2024). Inference of nonlinear causal effects with GWAS summary data. In Conference on Causal Learning and Reasoning. PMLR.

@inproceedings{dai2022inference,
  title={Inference of nonlinear causal effects with GWAS summary data},
  author={Dai, Ben and Li, Chunlin and Xue, Haoran and Pan, Wei and Shen, Xiaotong},
  booktitle={Conference on Causal Learning and Reasoning},
  pages={},
  year={2024},
  rganization={PMLR}
}