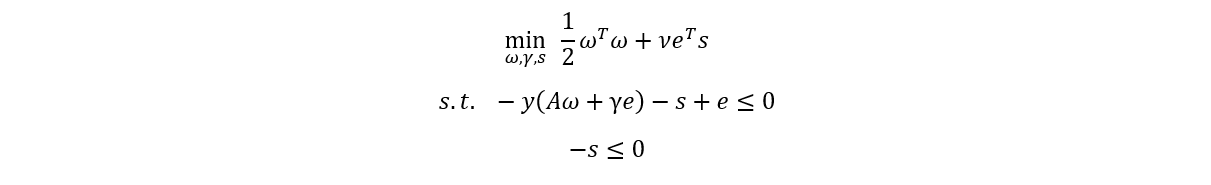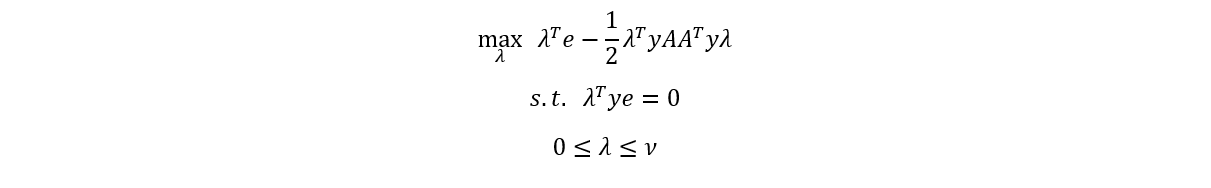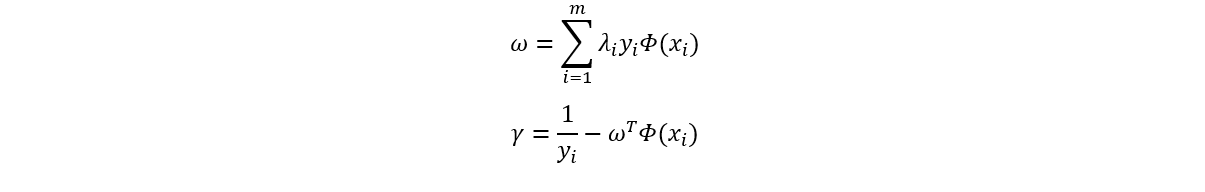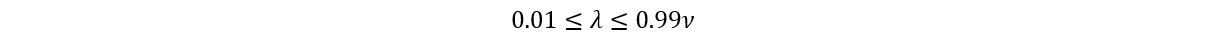marcelcases / svm-model

The mathematical model implementation of a Support-Vector Machine tested with a spam classification dataset

Support Vector Machine modeling

The objective of this project is to implement the primal and dual quadratic formulation of the Support Vector Machine in AMPL, and train and verify the models with a generated dataset and with a real one.

About

Course
Optimization Techniques for Data Mining (OTDM-MIRI)
FIB - Universitat Politècnica de Catalunya. BarcelonaTech
November 2021

Team

• Marcel Cases <[e-mail]>
• Mengxue Wang <[e-mail]>

Introduction

The goal of this laboratory assignment is to model the primal and dual formulations of a Support Vector Machine using AMPL. To test the models, a training set of 1000 random samples is generated, and then it is tested with a test set of another different 1000 samples. Furthermore, the models are tested with a real dataset of spam classification. The results are analysed and discussed.

Models

Primal

The mathematical formulation of the primal SVM problem is

Dual

The mathematical formulation of the dual SVM problem is

To calculate the separation hyperplane, we can retrieve ω and γ from the results obtained in the dual formulation as follows:

For calculating γ, we have to take any i such that y_i is a support vector point and not a misclassification or a near-binding point.

Implementation

Primal

AMPL code of the primal formulation (svm-primal.mod):

# Parameters
param n; 				# rows
param m; 				# columns
param nu;				# tradeoff

param y_train {1..m};        	# response value
param A_train {1..m,1..n};   	# feature values

param y_test {1..m};        	# response value
param A_test {1..m,1..n};   	# feature values

# Variables
var w {1..n};
var gamma;             	# intercept
var s {1..m};          	# slack


# Primal formulation
minimize primal:
	(1/2)*sum{j in {1..n}}(w[j]^2) +nu*sum{i in {1..m}}(s[i]);
	
subject to c1 {i in {1..m}}:
	-y_train[i]*(sum{j in {1..n}}(A_train[i,j]*w[j]) + gamma) -s[i] + 1 <= 0;

subject to c2 {i in {1..m}}:
	-s[i] <= 0;

Dual

AMPL code of the dual formulation (svm-dual.mod):

# Parameters
param n; 				# rows
param m; 				# columns
param nu;				# tradeoff

param y_train {1..m};        	# response value
param A_train {1..m,1..n};   	# feature values

param y_test {1..m};        	# response value
param A_test {1..m,1..n};   	# feature values

# Variables
var lambda {1..m} >= 0, <= nu;


# Dual formulation
maximize dual:
	sum{i in {1..m}}lambda[i] 
	-(1/2)*sum{i in {1..m}, j in {1..m}}lambda[i]*y_train[i]*lambda[j]*y_train[j]*(sum{k in {1..n}}A_train[i,k]*A_train[j,k]);
	
subject to c1:
	sum{i in {1..m}}(lambda[i]*y_train[i]) = 0;

Train

The models are first trained with the train dataset using the script below (contained in svm.run):

# Solve the primal
reset;
print "SVM_PRIMAL:";

model svm-primal.mod;
data "./data/spambase.dat"; #spambase #size100-seed66407 #size2000-seed75421

option solver cplex; #gurobi

problem SVM_PRIMAL: w, gamma, s, primal, c1, c2;
solve SVM_PRIMAL;
display w, gamma, s;


# Solve the dual
reset;
print "SVM_DUAL:";
model svm-dual.mod;
data "./data/spambase.dat";

option solver cplex;

problem SVM_DUAL: lambda, dual, c1;
solve SVM_DUAL;
display lambda;

AMPL code for computing ω and γ from the dual solution (contained in svm.run):

param w {1..n};
let {j in {1..n}} w[j] := sum{i in {1..m}} lambda[i]*y_train[i]*A_train[i,j];
display w;

param gamma;
for {i in {1..m}} {
	if lambda[i] > 0.01 and lambda[i] < nu*0.99 then {
		# A support vector point was found
		let gamma := 1/y_train[i] - sum{j in {1..n}} w[j]*A_train[i,j];
		break;
	}
}
display gamma;

Given that some solvers (e.g., Gurobi or CPLEX) calculate lambdas that are near to zero or ν, but are not equal to zero or ν (in near-binding and misclassified points), we have set the following safety boundaries to correctly identify the right support vector points:

Test

The models are then verified with a test dataset, and the accuracy of the models is calculated at the end of the execution. The following script contained in svm.run does whis workflow:

# Predict values with the test dataset
param y_pred {1..m};
let {i in {1..m}} y_pred[i] := gamma + sum{j in {1..n}}w[j]*A_test[i,j];
let {i in {1..m}} y_pred[i] := if y_pred[i] <= 0 then -1 else 1;
display y_pred;

# Check misclassifications
param misclassifications default 0;
for {i in {1..m}} {
	if y_pred[i] != y_test[i] then
		let misclassifications := misclassifications + 1;
}

display misclassifications;

param accuracy = (m - misclassifications) / m;
display accuracy;

Datasets

gensvmdat

The first dataset is generated with the tool gensvmdat. For this, 2000 pseudo-random samples were generated with the seed 75421. It contains just 4 features and a response value, which is +1 if the sum of the four features is greater than 2; -1 otherwise. This generator randomly introduces errors on the data. These samples were re-arranged in a way that is readable by the AMPL interpreter. The samples were split as follows: 1000 for training the models (A_train and y_train) and 1000 for testing them (A_test and y_test). The file is named size2000-seed75421.dat.

Spam Base

The second dataset is a real dataset. It is called spambase.dat and contains information for identifying spam. It contains 575 samples for training, 575 more for testing, and has 57 features. The feature values (A_train and A_test) contain information such as the average length of uninterrupted sequences of capital letters, or word frequency and repetition contained in emails. The response values (y_train and y_test) denote whether the e-mail was considered spam (1) or not (-1).

The source of the dataset is UCI Machine Learning Repository. The dataset was re-arranged to fit the requirements of the AMPL model, and was reduced from 4601 samples to 1150, chosen uniformly at random, for easing the computation.

Results and analysis

Given that SVMs are convex quadratic optimization problems, we have used CPLEX as the solver.

To run the whole training and test process, we call:

$> ampl: include svm.run;

gensvmdat

After some tests, we found that a value of ν = 5.7 offers a good tradeoff between misclassifications and the margin of the hyperplane, with the results below:

SVM_PRIMAL:
CPLEX 20.1.0.0: optimal solution; objective 1731.80453
12 separable QP barrier iterations
No basis.
w [*] :=
1  4.54128
2  4.73366
3  5.33484
4  4.95617
;

gamma = -9.71265

s [*] :=
   ... (1000 results hidden);
;

SVM_DUAL:
CPLEX 20.1.0.0: optimal solution; objective 1731.804529
25 QP barrier iterations
No basis.
lambda [*] :=
   ... (1000 results hidden);

w [*] :=
1  4.54128
2  4.73366
3  5.33484
4  4.95617
;

gamma = -9.71265

y_pred [*] :=
   ... (1000 results hidden)
;

misclassifications = 74

accuracy = 0.926

This value of the accuracy is what we would expect from this dataset, which was trained and tested with randomly generated errors in some of the response values.

Spam Base

A value of ν = 2.7 minimizes misclassifications, with the results below:

SVM_PRIMAL:
CPLEX 20.1.0.0: optimal solution; objective 270.1854038
22 separable QP barrier iterations
No basis.
w [*] :=
 1  0.0915065     16  0.683065      31 -0.17042       46 -2.01071
 2  0.0162915     17  0.304329      32 -0.15831       47 -0.00985572
 3 -0.188965      18  0.148016      33 -0.158999      48 -1.01895
 4  0.522129      19  0.106661      34  0.0562737     49 -0.959388
 5  0.142851      20  0.183208      35 -1.19706       50 -0.0961407
 6  0.425034      21  0.139132      36  1.20078       51  0.326661
 7  1.67436       22  0.297325      37 -0.417453      52  0.224816
 8  0.553699      23  0.840063      38  0.294852      53  2.83669
 9  1.1068        24  0.698235      39 -0.486375      54 -0.0302722
10  0.28966       25 -2.11514       40  0.309136      55 -0.0291872
11 -0.702934      26 -0.500174      41 -0.0291479     56  0.0112722
12 -0.0205462     27 -0.903876      42 -0.50297       57  0.000431733
13  0.387198      28 -0.654641      43 -0.922825
14  0.0346277     29 -0.606968      44 -0.536147
15  1.56212       30 -0.260752      45 -0.267816
;

gamma = -1.24035

s [*] :=
  ... (575 results hidden)
;

SVM_DUAL:
CPLEX 20.1.0.0: optimal solution; objective 270.185403
19 QP barrier iterations
No basis.
lambda [*] :=
  ... (575 results hidden)
;

w [*] :=
 1  0.0915249     16  0.683076      31 -0.170288      46 -2.0107
 2  0.0162924     17  0.304336      32 -0.158245      47 -0.00989798
 3 -0.188959      18  0.14803       33 -0.158996      48 -1.01889
 4  0.522147      19  0.106655      34  0.056406      49 -0.959302
 5  0.142849      20  0.183271      35 -1.197         50 -0.096141
 6  0.424988      21  0.139128      36  1.20072       51  0.326742
 7  1.67447       22  0.297294      37 -0.417524      52  0.224821
 8  0.553691      23  0.840089      38  0.294854      53  2.83691
 9  1.1069        24  0.698246      39 -0.48634       54 -0.0301934
10  0.289666      25 -2.11473       40  0.309192      55 -0.0291985
11 -0.702908      26 -0.500716      41 -0.029146      56  0.0112722
12 -0.020541      27 -0.903933      42 -0.50297       57  0.000431776
13  0.387196      28 -0.654655      43 -0.922947
14  0.034634      29 -0.606946      44 -0.536125
15  1.56216       30 -0.260704      45 -0.267806
;

gamma = -1.24035

y_pred [*] :=
  ... (575 results hidden)
;

misclassifications = 40

accuracy = 0.930435

The accuracy for this dataset is acceptable. The high dimensionality of this dataset (R⁵⁷) allows the hyperplane to be more optimal than in cases with reduced dimensionality.

The number of iterations needed for computing the dual solution (19) is lower than the iterations needed for the primal (22).

Conclusions

The tests performed show that both the dual and the primal versions of the SVM converge to the same results. The separation hyperplane calculated from the dual model is always the same hyperplane as in the primal model. We can use the most convenient version depending on the dataset. For larger datasets, the dual problem is usually faster than the primal.

References

Task statement
Class slides
AMPL documentation
Nocedal, J.; Wright, S.J. Numerical optimization