SwissGL: Swiss Army knife for WebGL2

DEMO

SwissGL is a minimalistic wrapper on top of WebGL2 JS API. It's designed to reduce the amount of boilerplate code required to manage GLSL shaders, textures and framebuffers when making GPGPU-style procedural visualizations or simulations. See the demos for examples of using SwissGL. As of now the library consists of a standalone ~500 loc .js file.

Disclaimer This is not an officially supported Google product. SwissGL is an early stage experiment, incomplete and unstable. It's an invitation to discuss compact and expressive graphics library design, which I hope is relevant in light of the upcoming arrival of WebGPU.

Quickstart

As of now, the library API consists of a single function object that does everything (like a Swiss Army knife). Here is a minimal example of using it to draw an animated gradient quad:

<script src="swissgl.js"></script>
<canvas id="c" width="600" height="400"></canvas>
<script>
    const canvas = document.getElementById('c');
    const glsl = SwissGL(canvas);

    function render(t) {
        t /= 1000; // ms to sec
        glsl({t}, `P,cos(t*TAU),1`);
        requestAnimationFrame(render);
    }
    render();
</script>

This line creates a SwissGL library instance that wraps a WebGL2 context of a given canvas element (you can also pass a WebGL2 context):

const glsl = SwissGL(canvas);

Now we can already draw something:

glsl({t}, `P,cos(t*10.0),1`);

This line, called during the animation loop, creates a shader that evaluates the given expression string into RGBA-color for every pixel on the canvas. vec2 P variable provides [0,1]-range normalized coordinates of the current pixel, and ivec2 I can be used to get integer coordinates. The shader is compiled and cached during the first call and reused later.

glsl function has at most three arguments, some of which can be omitted:

glsl(params, code, target);

Please refer to the API section below for the detailed explanation of their function. Let's now have a look at the more elaborate example of using SwissGL to implement a particle simulation.

Particle Life

Inspired by the beautiful video by Tom Mohr, let's try reproduce the "snake" pattern shown there. Particle Life is made of particles of a few different types. All particles repel when they are closer than some distance $r$, but at around $2r$ the resulting (potentially non-symmetric) force is described by the special force matrix $F_{i,j}$, where $i,j$ are types of two particles. Positive $F$ corresponds to attraction and negative to repulsion. Let's create a texture that stores such a matrix. We can create an array on the JS side and pass it to SwissGL, but it's even easier to populate matrix values right on GPU:

const K = 6; // number of particle types
const F = glsl(`
    float(I.x==I.y) + 0.1*float(I.x==I.y+1)`,
    {size:[K,K], format:'r16f'});

This creates a single channel float16 texture of size [width,height]==[6,6] and populates its values by evaluating the expression. I is a special variable of type ivec2 that contains coordinates of the pixel being evaluated.

We can easily visualize the resulting texture to make sure everything is ok:

glsl({F}, `F(I/20).x*3.0`);

Uniform textures can be accessed with usual GLSL functions, or with a helper macro that has the same name as the texture uniform. Passing ivec2 as parameter makes it call texelFetch() to get a texel using the integer coordinates, passing vec2 uses texture(), with filtering and wrapping.

The next step is to create a list of textures that is going to contain particle positions. Each pixel will contain a single particle position and type.

const points = glsl({size:[30,10], story:3, format:'rgba32f', tag:'points'});

We are going to simulate 30*10=300 particles. Textures will have 4 channels (RGBA) of type float32. The story:3 argument says that we need to create a cyclic buffer of three textures of the same format, so that we can read two consecutive states of the particle system (for momentum) to produce the third. We don't provide shader code to the SwissGL call, so we must specify the storage tag. Now we can initialize these textures:

for (let i=0; i<2; ++i) {
    glsl({K, seed:123}, `
        vec2 pos = (hash(ivec3(I, seed)).xy-0.5)*10.0;
        float color = floor(P.x*K);
        out0 = vec4(pos, 0.0, color);`,
        points);
}

The shader code above uses "multiline" shader code format instead of a single expression. The output must be written to a global variable out0. Variable P has type vec2 and provides [0,1]-range normalized coordinates of the current pixel. It is used to assign one of K "colors" to each particle. For convenience SwissGL provides a simple hash function vec3 hash(ivec3) that can be used as a deterministic random number generator.

Note that we are writing the same particle positions two times, which means that particles have zero velocity at initialization. Now points[0] and points[1] contain the same values, and points[2] is uninitialized and is going to be overwritten at the first simulation step.

Before we start modeling the particle dynamics it's a good idea to implement visualization. So far we've already seen "expression" and "multiline" shortcut code formats. Now we are going to write a full vertex-fragment shader pair:

glsl({K, worldExtent,  // uniforms
      // reading the last state of 'points' texture
      points: points[0], 
      // render a quad instance for every 'points' texel
      Grid: points[0].size,
      // preserve the scale of xy-axes by fitting
      // [-1..1]x[-1..1] box into the view
      Aspect:'fit',
      // blend primitives using alpha transparency
      Blend: 'd*(1-sa)+s*sa'}, `

// the code below is available in both
// vertex and fragment shaders
varying vec2 r;
varying vec3 color;

//VERT  start of vertex-only section
// vertex function is called 
vec4 vertex(vec2 uv) {
    // get current particle data
    vec4 d = points(ID);
    // populate varyings to use in fragment shader
    color = cos((d.w/K+vec3(0,0.33,0.66))*TAU)*0.5+0.5;
    r = uv-0.5;
    // emit normalized on-screen vertex position
    return vec4(2.0*(d.xy+r*0.25)/worldExtent, 0.0, 1.0);
}

//FRAG  start of fragment-only section
void fragment() {
    // compute the fragment transparency depending
    // on the distance from the quad center
    float alpha = smoothstep(0.5, 0.3, length(r));
    // set the fragment color
    out0 = vec4(color, alpha);
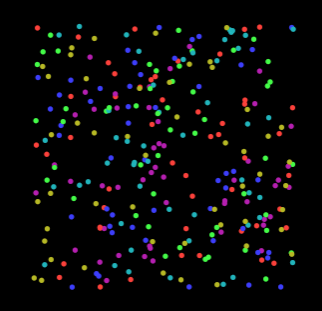
}`); // 'target' is omitted, so rendering to canvas

Running this code in the drawing loop produces the following image:

The vertex shader computes WebGL Clip Space coordinates for each corner of each particle quad. We map particle positions from [-worldExtent/2, worldExtent/2] range to [-1,1] box. This shader also computes particle color using cosine palettes trick and passes it to the fragment shader along with the corner offset vector. The fragment shader calculates pixel opacity alpha using the distance form the particle center and sets out0 variable. This way we can use low-level GLSL as an expressive, flexible and performant tool to render large numbers of primitives.

Now we can set particles in motion by writing the update shader that computes new particle positions each frame.

glsl({F, worldExtent, repulsion, inertia, dt, // uniforms
      // The current state of the system is implicitly
      // available to the shader as 'Src' uniform if
      // the target has history (is an array of textures).
      // Here we explicitly pass the state one step at the past
      past:points[1]}, `
// this function wraps positions and velocities to
// [-worldExtent/2, worldExtent/2] range
vec3 wrap(vec3 p) {
    return (fract(p/worldExtent+0.5)-0.5)*worldExtent;
}
void fragment() {
    // read the current particle state
    out0 = Src(I);
    vec3 force=vec3(0); // force accumulator
    // iterate over particles
    for (int y=0; y<ViewSize.y; ++y)
    for (int x=0; x<ViewSize.x; ++x) {
        // reading the state of another particle
        vec4 data1 = Src(ivec2(x,y));
        vec3 dpos = wrap(data1.xyz-out0.xyz);
        // calculate distance
        float r = length(dpos);
        if (r>3.0) continue;
        dpos /= r+1e-8;
        // calculate repulsion and interaction forces
        float rep = max(1.0-r, 0.0)*repulsion;
        float f = F(ivec2(out0.w, data1.w)).x;
        float inter = f*max(1.0-abs(r-2.0), 0.0);
        force += dpos*(inter-rep);
    }
    // fetch the past state to compute velocity
    vec3 vel = wrap(out0.xyz-past(I).xyz)*pow(inertia, dt);
    // update particle position
    out0.xyz = wrap(out0.xyz+vel+0.5*force*(dt*dt));
}
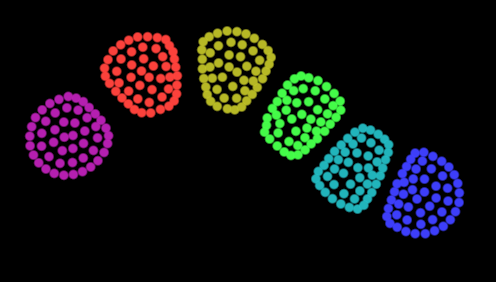
`, points);  // using 'points' as the target

Soon randomly scattered particles self-assemble into a nice colorful snake! The simulation is happening on the GPU and is quite fast for the quadratic complexity algorithm (that iterates all particle pairs). Even mobile phones can run hundreds of steps per second. Thanks to SwissGL, orchestrating this computation, managing shaders and framebuffers takes minimal amount of boilerplate code.

API

glsl function has at most three arguments, some of which can be omitted:

glsl(params, code, target);

params is a dictionary that is mainly used to pass uniforms to the GLSL program. It may also contain a few special arguments (see below) that control the WebGL state, like blending or clear the buffer before the draw call. SwissGL tries to automatically infer uniform types and introduce them to the shader code (it's also possible to override the types by declaring uniforms manually).
code is a string that contains GLSL code. Whenever a non-empty string is passed, SwissGL will try to expand it into a pair of vertex and fragment shaders, compile and link them and cache the resulting shader program for future use. Cached shaders are stored in the glsl.shaders dictionary. Then the library will execute a WebGL draw call using this program. The type and the number of drawn primitives is controlled by the Mesh and Grid special arguments in params (see below).
target determines the buffer where the rendering results are written. These are the following possibilities:
- null or undefined - render to canvas directly.
- WebGLTexture object - render to the texture.
- Array of WebGLTexture's - render to the last texture in the array and cyclically shift the array in-place so that it becomes element 0. This is useful for ping-pong buffers where element 0 corresponds to the state of the system at the current time step, element 1 to the previous step and so on. The original 0-th texture is provided to the shader for reading as Src uniform for convenience.
- Texture specification dictionary. That's how we can use SwissGL to create new textures or even arrays of textures. Like shaders, textures are cached in the glsl.buffers dictionary. tag attribute of the specification is used as a key. Shader code is used when tag is not provided.

glsl function returns a reference to the target. If the texture specification was given, the actual created texture(s) is returned.

Special arguments

In addition to uniforms, SwissGL accepts a number of options in the params argument. These options control the WebGL state and the number of rendered primitives:

Clear: scalar or [r,g,b,a] array. Clears the target buffer with a given color before rendering. Also clears the depth buffer if it's present. (TODO: option to keep depth)
Blend: string. Expression that controls WebGL blending mode (set with gl.blendFunc and gl.blendEquation). Inputs are: s - source color emitted by fragment shader; d - destination color already present in the target buffer; sa - source alpha; da - destination alpha. Examples: s+d, d-s, d*(1-sa)+s*sa (standard transparency), d*(1-sa)+s (premultiplied alpha), max(s,d), min(s,d), d*s. (TODO formal language definition)
View: array [w, h] or [x, y, w, h]. Controls WebGL viewport. By default viewport is set to cover the whole target. Value is available in shader as uniform ivec4 View. ViewSize macro also provides ivec2 view size.
Aspect: string (fit, cover, mean, x, y). Adjust xy coordinates emitted by vertex the program to preserve the scale of viewport axes.
Grid: [w, h], default [1,1]. instantiate the rendered primitive w*h times. Instance ID is available in the vertex shader as ivec2 ID. Grid size is available in shader as uniform ivec2 Grid.
Mesh: [w, h], default [1,1]. Tessellate the rendered 2d plane primitive. vec2 uv argument provides [0,1]-range normalized vertex coordinates. Integer vertex index is also provided as ivec2 VID variable. Mesh size is available in the shader as uniform ivec2 Mesh.
DepthTest: enable gl.DEPTH_TEST if true.
AlphaCoverage: enable gl.SAMPLE_ALPHA_TO_COVERAGE if true. See this article for the usage example.
Perspective: TODO rework

Code formats

SwissGL accepts a code string that contains a pair of vertex and fragment shaders together, which we call full format. In addition to that, there is a number of shortcuts that are mainly used for full-screen/buffer quad rendering:

expression: a string that becomes correct expression if it's substituted into vec4(${code}) template.
multiline: a function body that can be substituted into void fragment() { ${code}; } template. The output must be written into the out0 variable of type vec4.
fragment: a piece of GLSL code that contains a void fragment() {...} function. This format allows defining additional functions or custom uniforms.
full: a concatenated pair of vertex and fragment programs in a special form. Full code format, combined with Mesh and Grid arguments, enables rendering much more sophisticated objects than simple full-screen quads. Here is a minimal example:

varying vec2 vUV;
//VERT
vec4 vertex(vec2 uv) {
    vUV = uv;
    return vec4(uv*2.0-1.0, 0.0, 1.0);
}
//FRAG
void fragment() {
    out0 = vec4(vUV, 0.0, 1.0);
}

Target specification

The following options control the creation of new textures:

size: [w,h] size of the created texture. Also affected by scale option. Set to the canvas size by default. Can be modified after the target creation.
scale: scalar. Coefficient applied to size before creating the texture. For example the following specification {scale:1/4} will create a target that is four times smaller that the canvas frame buffer in each dimension, and is automatically resized on canvas size changes.
format: string, rgba8, r8, rgba16f, r16f, rgba32f, r32f are currently supported.
data: TypedArray of size and type matching the texture specification. Allows to set the texture content from JS and update it after the texture creation to stream the new data to GPU. See Spectrogram demo for example.
tag: string that is used to cache the created texture in glsl.buffers. Shader code is used if not provided.
story: interger. Create an array of textures of the same format instead of a single one. Rendering to such target rotates the array in place so that the texture last rendered into becomes the element 0.
filter: 'nearest' or 'linear'
wrap: 'repeat', 'edge' or 'mirror'

Links

Sources of wisdom:

Playgrounds:

Libraries

lp249839965 / swissgl