CS518 Class Project

A Computational Geomemtry Class Project that implements DCEL data struture and Polygon triangulation as well as Plannar point location using persistent search trees.

Guangyu Hou

4/8/2017

Configuration/installation instructions

The program was written in C++ and implemented in Visual Studio 2013. It is developed in the Debug/x64 configuration. It uses OpenGL, especially the freeglut library to display the polygons. If you use visual studio 2013, you could directly open the solution file and run.

While compiling source code, be sure to include the freeglut header/lib/dlls in your project directory. While run the executable file, be sure to include freeglut.dll in the same folder.

Operating instructions

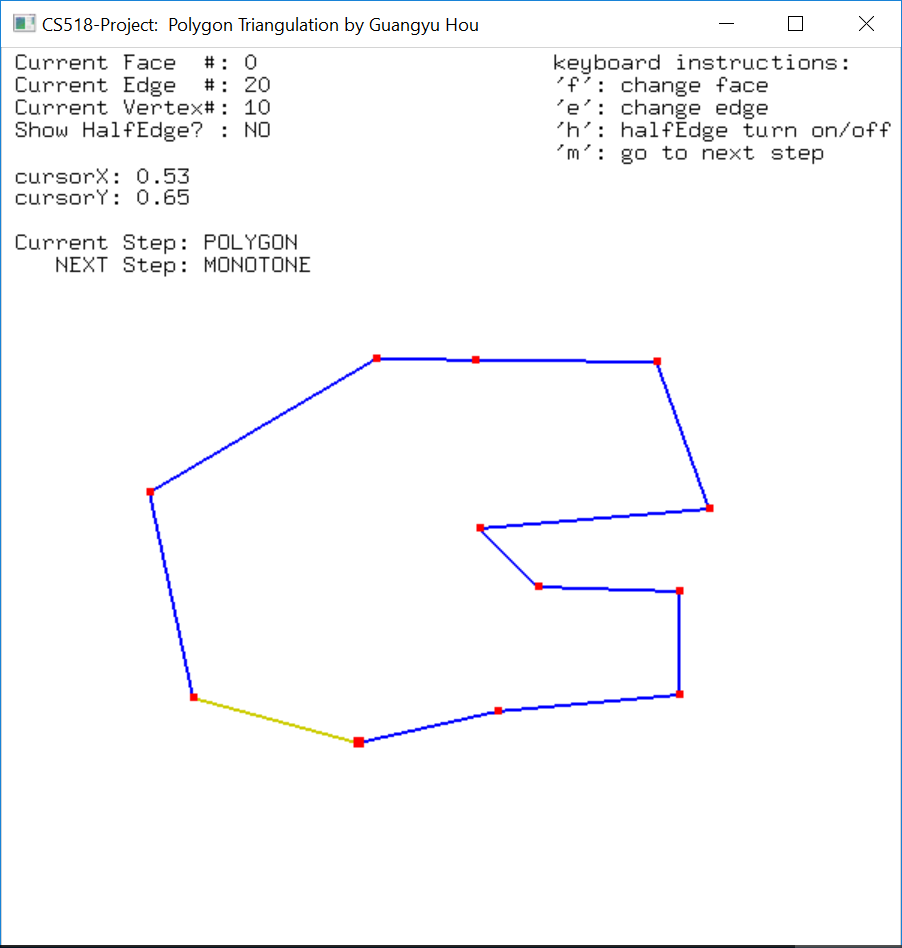
I have provided a user-friendly console that takes input, as show below:

The user needs to specify two things:

Which sample to test (sample choice) and
Which case to test (case choice).

The first three samples provided are three predefined sets of vertices, as shown below.

Polygon 1 Polygon 2 Polygon 3 User defined polygon

The user can choose one of them (1-3) and continue.

The four test cases are basically the implementation of

Construct simple polygon from the vertices set
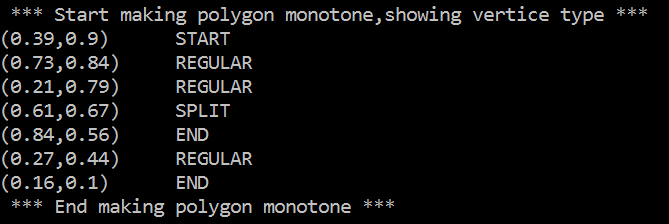
Make a simple polygon monotone
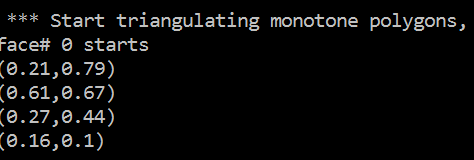
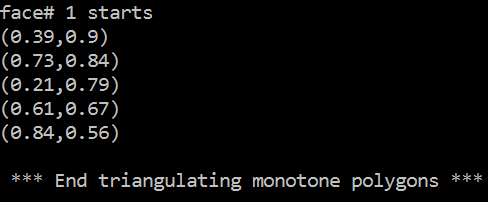
Triangulate all monotone polygons in the DCEL
Triangulate a specific monotone polygon specified by the user.

For example, if the user select sample 3, and run test case 1, 2, 3 respectively, he/she will get the following display: 1.Construct_simple_polygon()

2.Make_Monotone()

3.Triangulate_monotone_polygon()

Note that the user can modify the coordinates of these vertices in the program to test for most situations. To do this, go to the testcases.cpp, find runTestCases() function and modify the vertices coordinates in either of the variables list1, list2 or list3.

I have also provided a more convenient option: the user can select option 4 in sample choice, and provide vertices by clicking on the screen. Once all vertices are provided, press ‘M’ key on keyboard to form a polygon. Keep pressing ‘M’ key would lead to “Make monotone”, “Triangulation” and come back to “Provide vertices” step, which enables multiple tests.

Please node if you enter any of the 4 sample choices, you cannot go back to select another one, if you want to switch between them, please close the program and restart.

Point Location

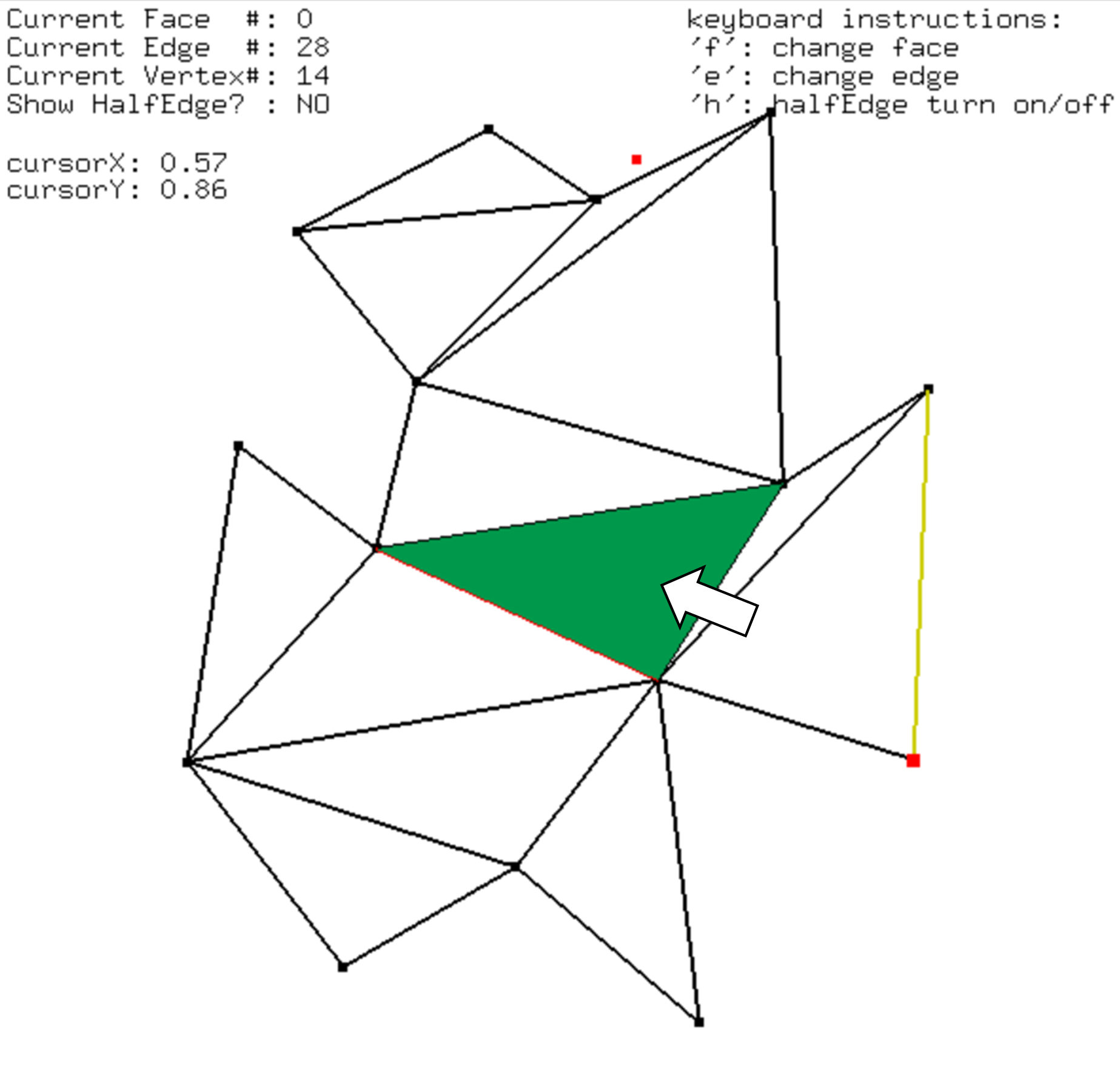
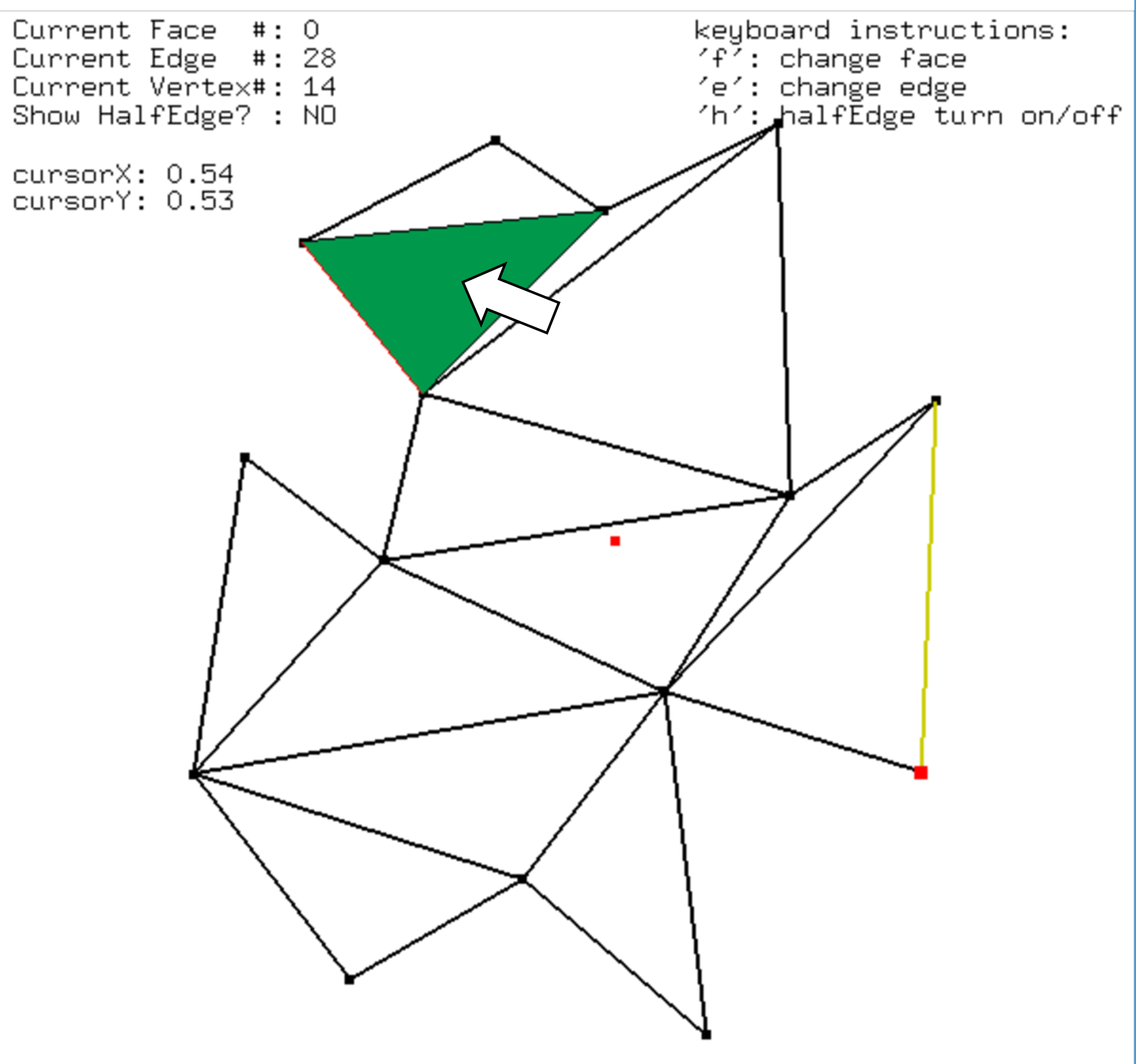
After the triangulation, the user can click on the screen which activates the query for the location of the point. The triangle that contains the point will be highlighted in green. The user can click multiple times on the screen and see the results. Note, the point location function works in all of the four sample choices. Below is an example:

Advanced user control

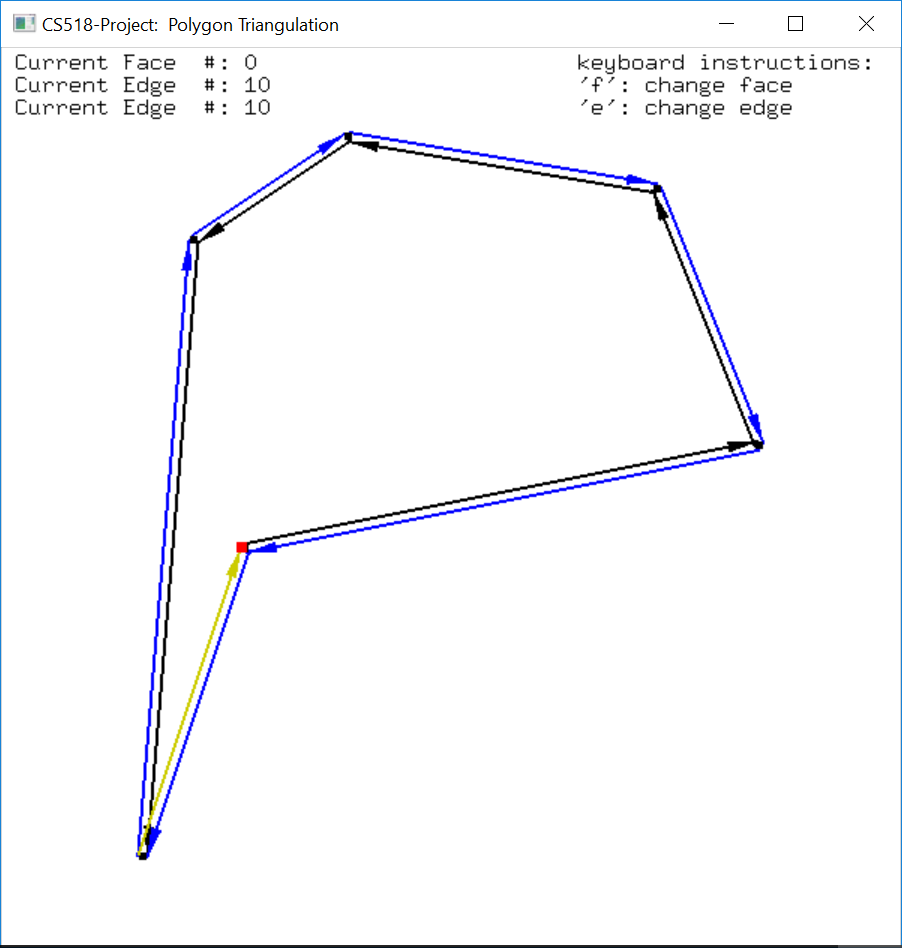
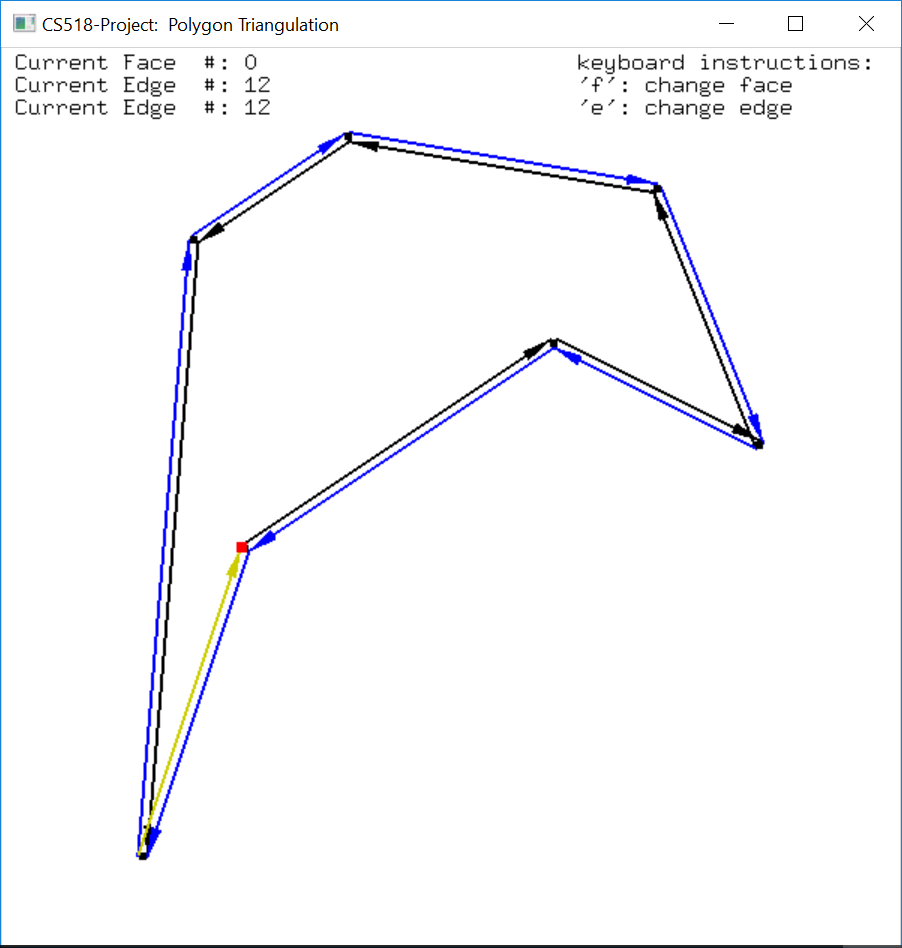
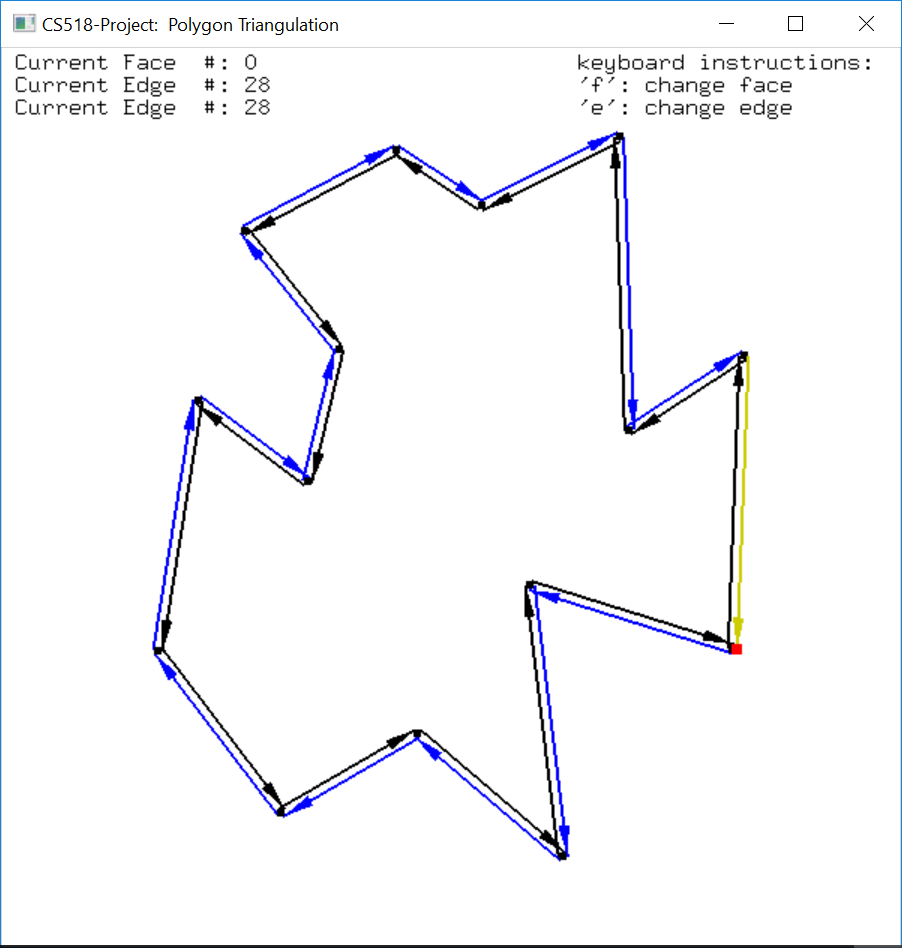
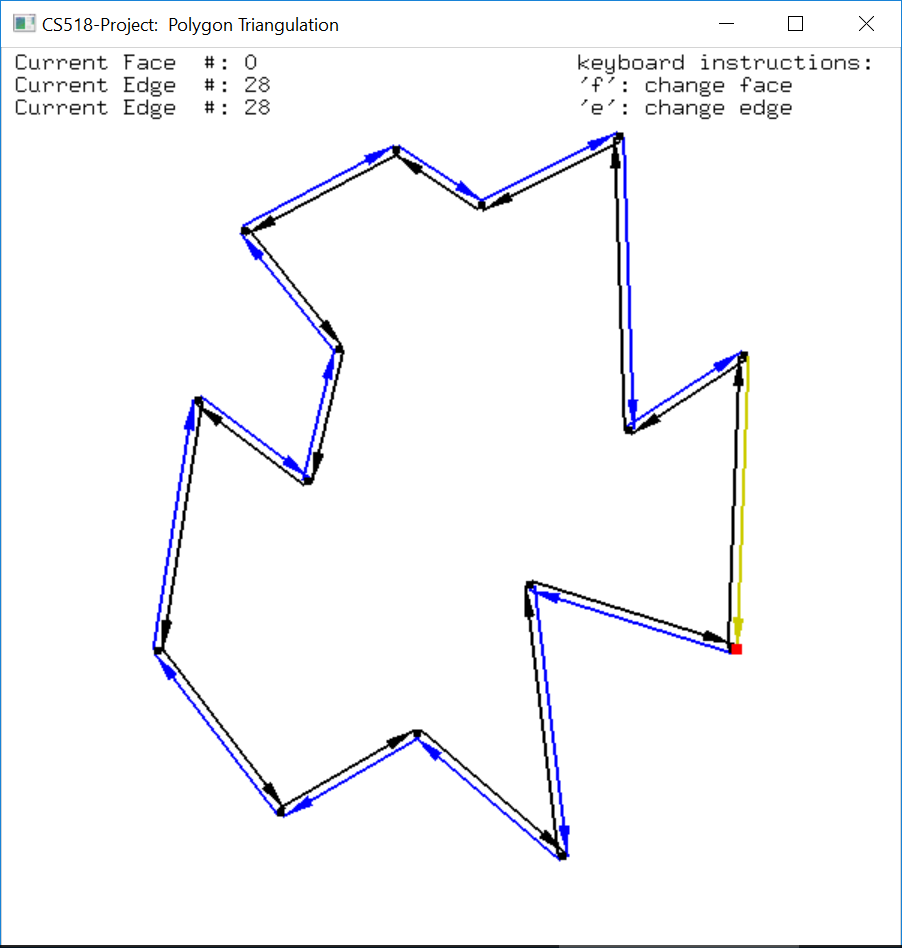
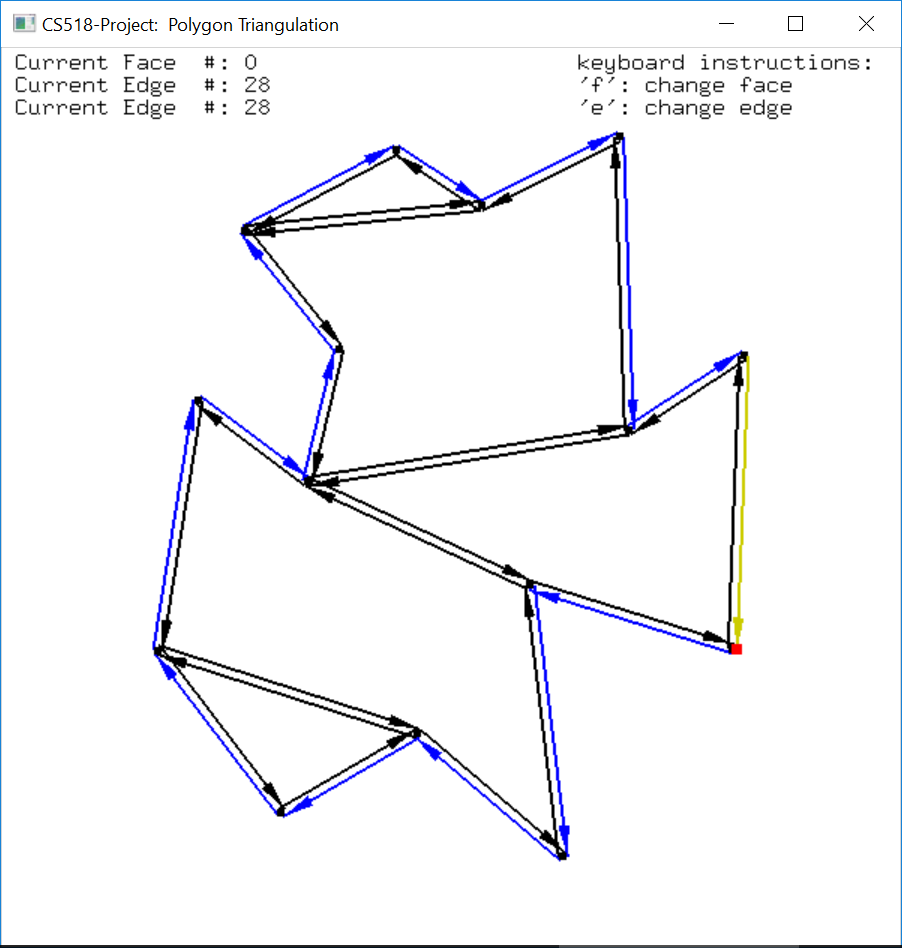
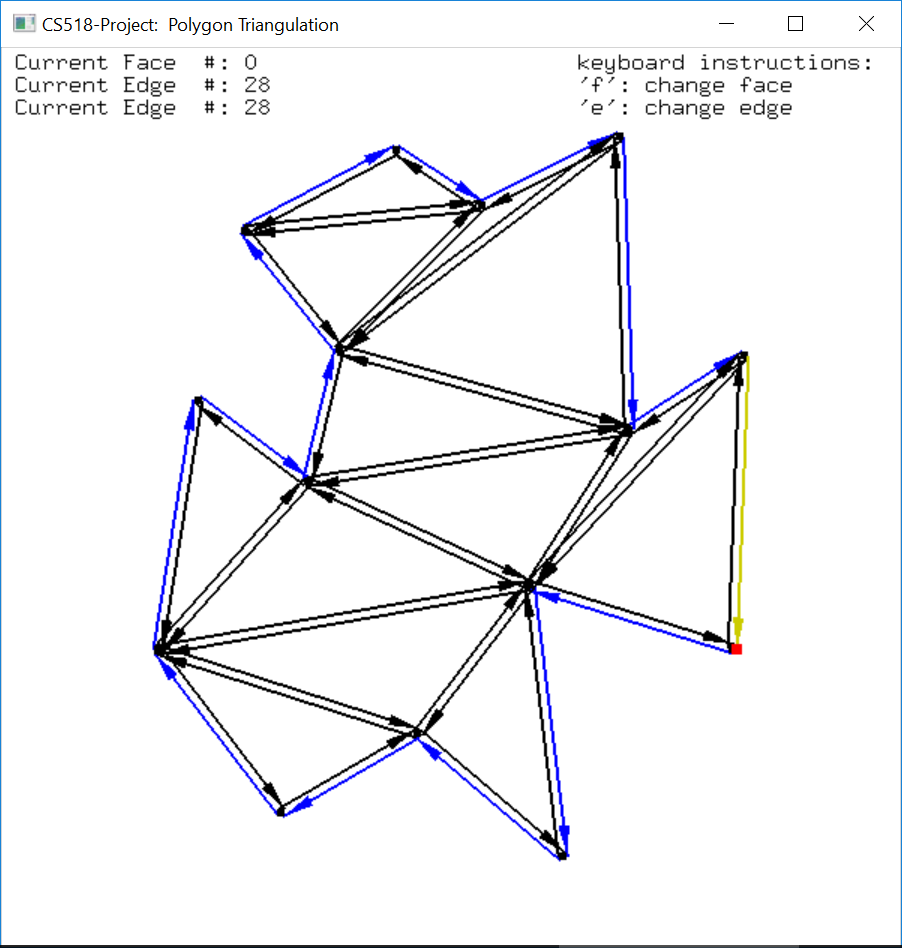
In the display, each edge is represented by two arrows indicating the two half-edges. The arrows follow the counterclockwise direction for outer component (in black) and clockwise direction for inner component (in blue). To switch on/off this functionality, press ‘H’ key.

There is also a yellow edge shown on the polygon. It is highlighted where the user can move it to traverse the boundary of different faces. To move it to the next edge, press ‘E’ key on keyboard, to change a face, press ‘F’ key on the keyboard. The destination vertex of the highlighted edge is shown in red.

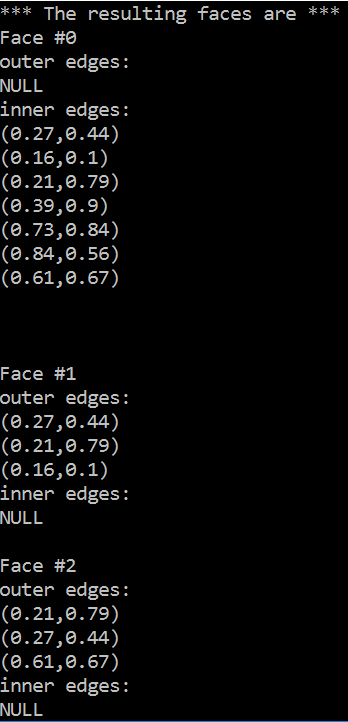
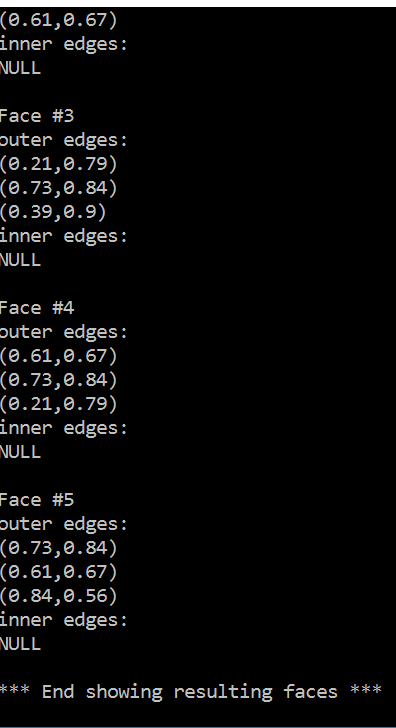
The data of the vertices, edges and faces of the DCEL structure is stored in three lists, one for each type. Therefore, each vertex/edge/face has its unique location in the list, if we traverse from the beginning of the list to the end, each item should have a number (distance from the font node) defining its position, like an array. This position information is showed on the top left of the display window indicating which face/edge/vertex the current highlighted edge is on.

Besides the GUI, the console has also shown useful information.

The vertices types in the method to make simple polygon monotone
The vertices’ coordinates of each monotone polygon to be triangulated
The resulting triangulation (in terms of vertices of each face)

List of files included

Freeglut ( headers/libs/dlls )

freeglut.h, freeglut_ext.h, greeglut_std.h, glut.h, freeglut.lib, freeglut.dll

Main program

The DCEL class (in DCEL.h and DCEL.cpp)

To add a vertex, use

void add_vertex_at(const Vertex& v, Edge* e);

To add an edge, use

void split_face(Vertex* v1, Vertex* v2);

To construct a simple polygon from a set of vertices, use

void construct_SimplePolygon(const vector<Vertex>& list);

The implementation of the first two functions can be referred to the source [1] and most functions in this project can be referred to the Dr. Baca’s class notes and the book [3].

The Triangulation class (in Triangulation.h and Triangulation.cpp)

To make a simple polygon monotone, use

void makeMonotone( DCEL& simpleP);

To triangulate a monotone polygon, use

void triangulate_MonotonePolygon( DCEL& P, int nFace = 1, Face* ptr = nullptr);

where the monotone polygon is a face in P, and you either specify its index or provide its address in P.

To triangulate ALL monotone polygons in the DCEL, use

void triangulate_simple_Polygon(DCEL& simpleP);

The Treap class (in Treap.h, MyTreap.h and MyTreap.cpp)

To facilitate Triangulation method. I use Treap balanced binary search tree as the underlying data structure to maintain the edge status. The base Treap class is in Treap.h. The code is largely from the source [2] and modified to fit the purpose in this project. The actual Treap used in the project is in MyTreap.h where it implements the method to locate an edge directly to the left of a given vertex. The detailed implementation is in MyTreap.cpp.

The PointLocation class (in PointLocation.h and PointLocation.cpp )

To find which triangle a given vertex lies in, a PointLocation class was developed. It basically uses two binary search trees, one for the slabs, one for the edges in a slab. Therefore, it leads to a query time complexity of (O(\log n)) and space requirement of (O(n^{2})), where (n) is the number of line segments of the planar subdivision. Due to lack of time, the persistent search tree for the point location problem is not implemented but can be done later.

To find a face that contains the vertex, use

Face* find_face_contains_vertex(DCEL* P, Vertex& v);

Running Time

The find, insert and delete operation of the Treap takes expected (O(\log n)) time. Where (n) is the number of edges.
The running time for make polygon monotone is (O(n\log n)) and uses (O(n)) space.
The running time for triangulate a monotone polygon is expected (O(n\log n)) as the Treap is used as the edge status tree. It uses (O(n)) space.
In summary, the triangulation can be implemented in expected (O(n\log n)) time and (O(n)) space.
The point location class has query time complexity of (O(\log n)) and space requirement of (O(n^{2})).

Known limitations and bugs

For the DCEL, when adding a vertex, it assumes the vertex and the edge it’s connecting are incident on the same face. Also, it assumes there is no intersection once an edge connecting the vertex is added.
For the DCEL, an edge can only be added if the two vertices defining it, share a face. If not, an exception is throw. To fix this, if two vertices does not share a face, I need to first find the intersection points, create vertices on those intersected edges and then add edges accordingly.
Point location class is implemented but not using a persistent search tree as the underlying data structure leading to higher space requirement (O(n\log n) \rightarrow \ O(n^{2})).
For the functions required in the project, the code runs fluently.

Credits and acknowledgments

[1] Plane graph and DCEL. https://www.ti.inf.ethz.ch/ew/lehre/CG12/lecture/Chapter%205.pdf

[2] Treap data structure, http://iss.ices.utexas.edu/projects/galois/api/2.1/treap_8h.html

[3] De Berg, M., Cheong, O., van Kreveld, M., and Overmars, M., 2008, "Computational Geometry: Algorithms and Applications."

houes / CS518_Project