This repo contains implementations of a collection of discrete differnetial geometry algorithms. They are based on a C++ skeleton code for the course assignments from Discrete Differential Geometry (15-458/858).
This code framework uses Geometry Central for geometry processing utilities and Polyscope for visualization, which were developed by Nick Sharp and others in the Geometry Collective. Also, It must be acknowledged that most of the illustrations used in this readme come from the course notes text provided with the mentioned course by Keenan Crane.
Below are the highlights of the implemented algorithms.
Given a mesh stored as a Halfedge structure, this part required building the incidence matrices and vector encodings for the mesh and its elements. These were then used to implement simple selection operations like Closure, Star, Link and boundary, as well as some simple boolen checks on a subcomplex of the mesh (isComplex(() and isPureComplex())
| Operator | Results (GIFs) |
|---|---|
Star & Closure  |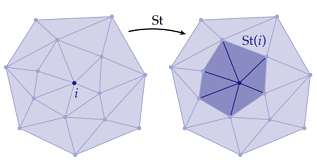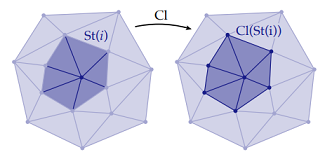
Can use them together repeateadly to grow a selection. |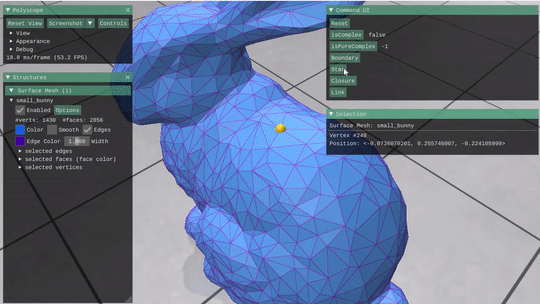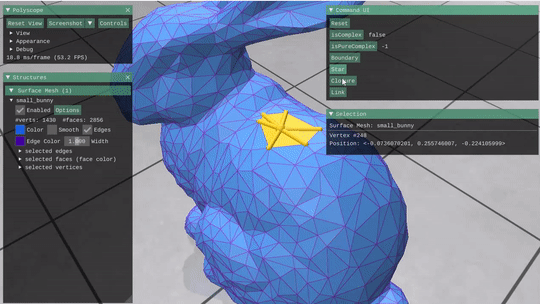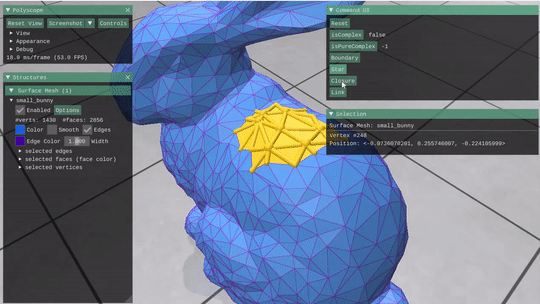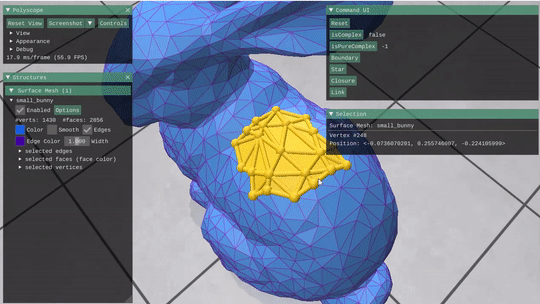
Link & Boundary  |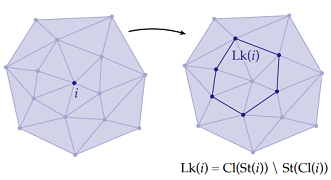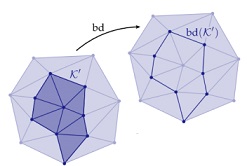
Can think of as an exclusive vs inclusive boundaries |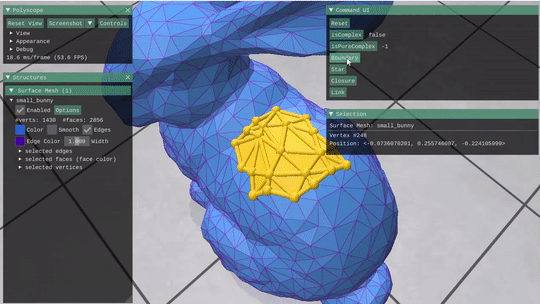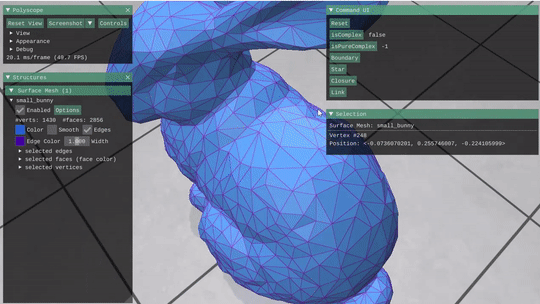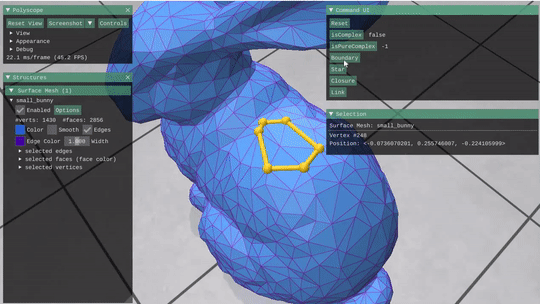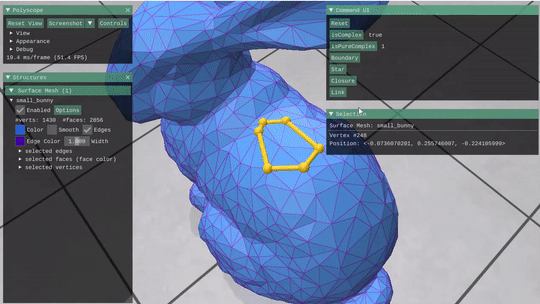
I got to learn about the discrete exterior calculus operators. The implementation of the discrete exterior derivative and the discrete Hodge star operators mainly involved implementing cotan() and barycentricDualArea() functions and using them to compute the discrete exterior derivative and the discrete Hodge star operators as matrices.
| Operator | Results (GIF) |
|---|---|
Exterior Deravtive & Hodge Star  |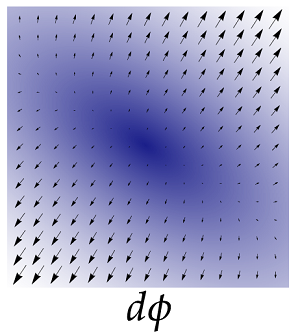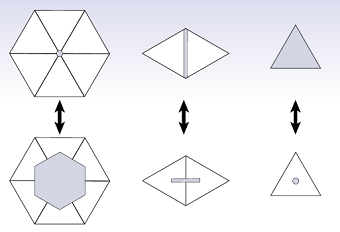
 |
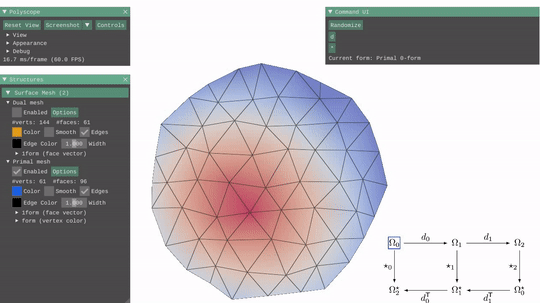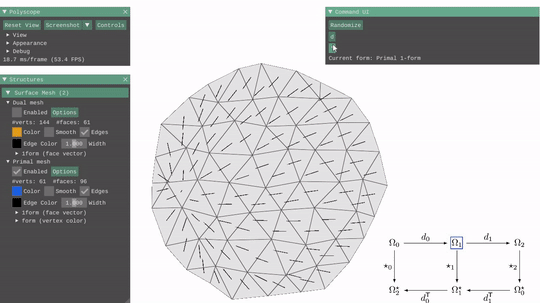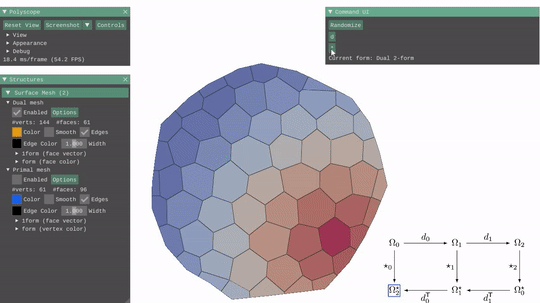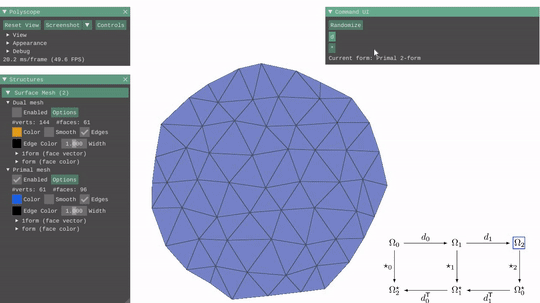I learned about a variety of ways to compute vertex normals, some of which are based on weighted averages of neighboring face normals. I also implemented the computation of the mean and Gaussian curvatures. These two were used to compute the principal curvatures.
| Algorithm | Results |
|---|---|
Vertex Normal Computation Methods |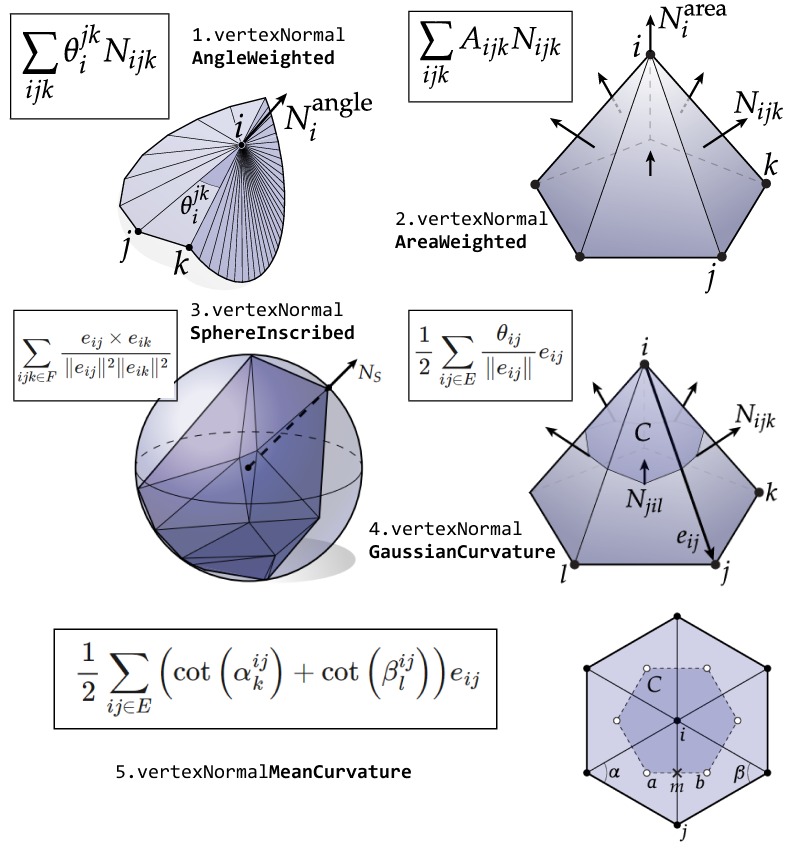
 |
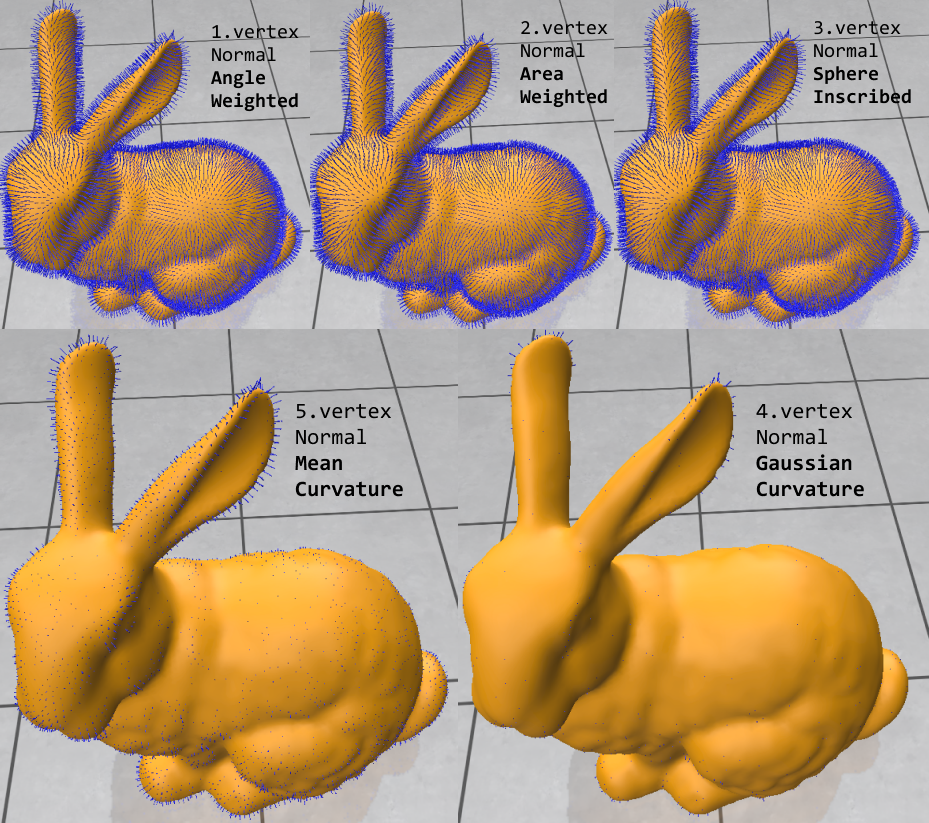Curvatures Computation  |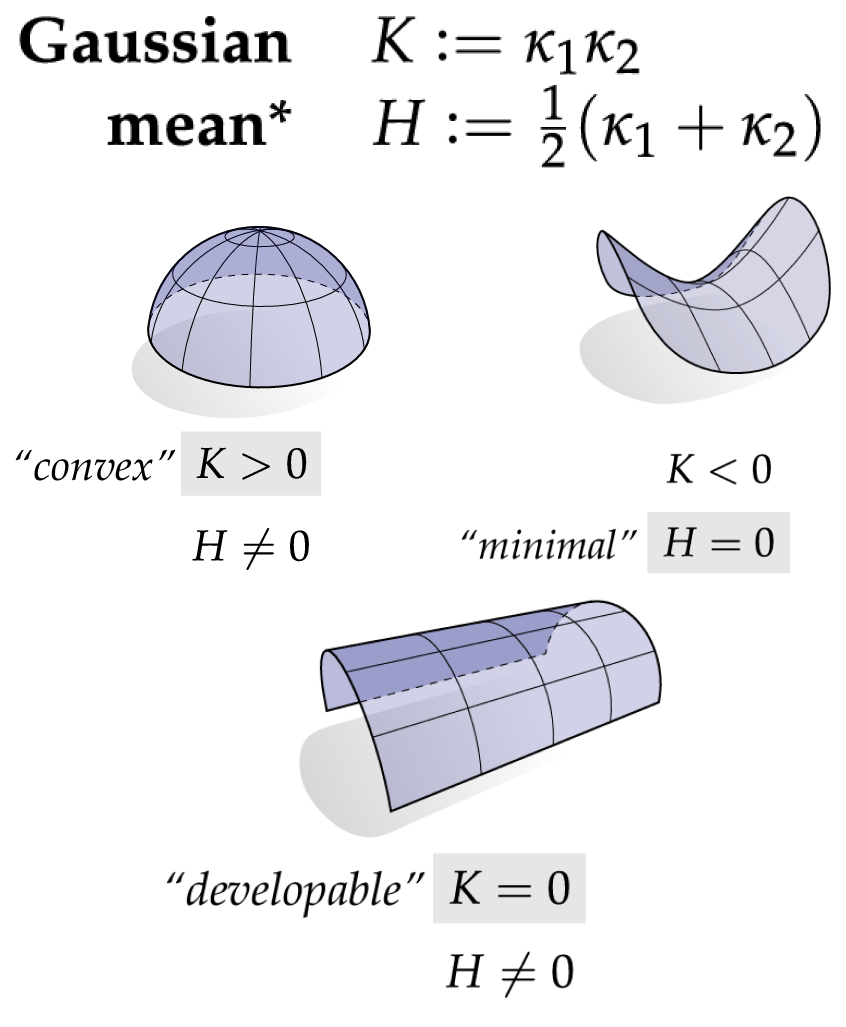
kmin & kmax: Mean & Gaussian Curvature:  |
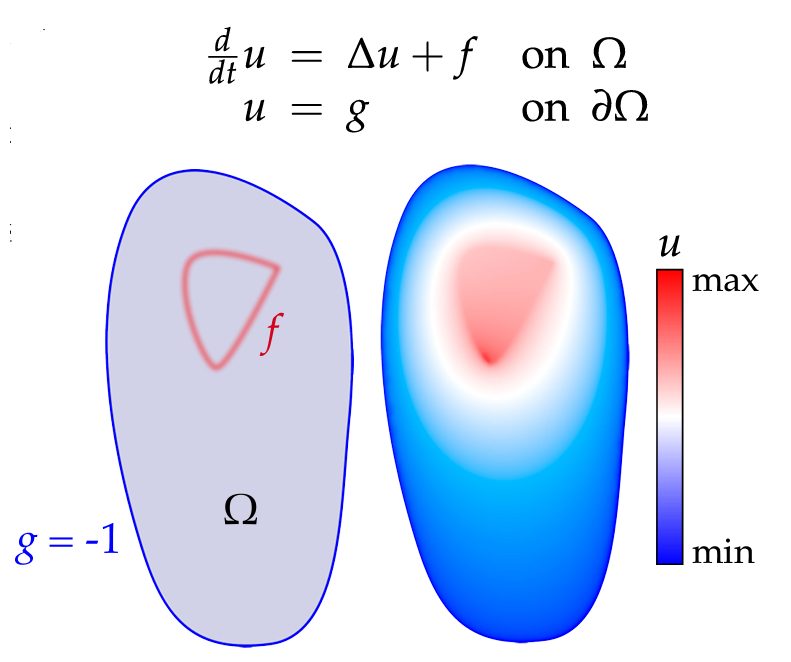
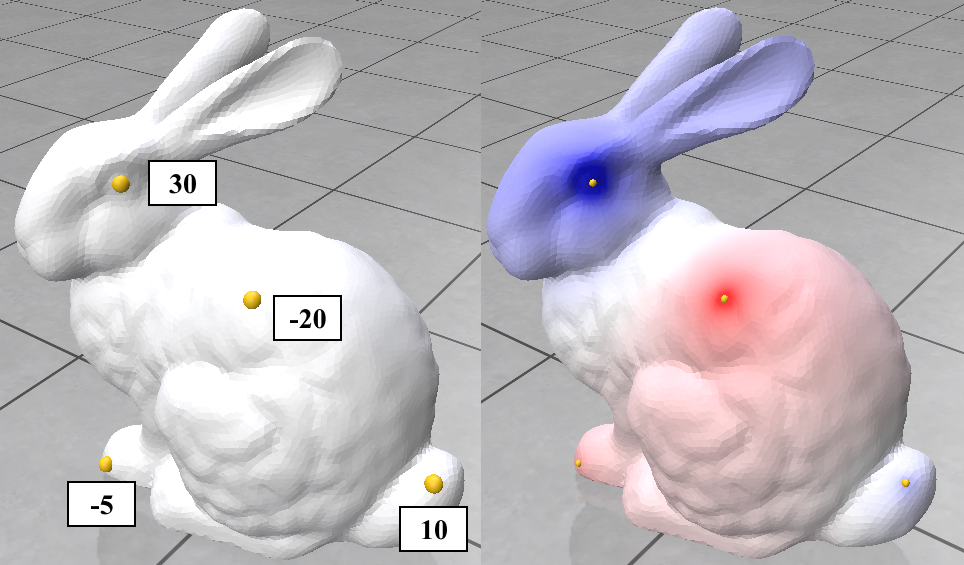
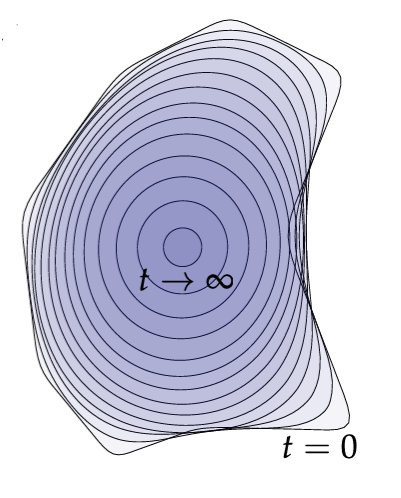
I got to implement the Laplace-Beltrami based on the cotangent Laplacian. It was used to implement the Poisson equation solver which was used to smoothely interpolate a function on the mesh. It was also used to implement mesh smoothing using the mean curvature flow and the stationary Laplacian mean curvature flow.
| Algorithm | Results (GIFs) |
|---|---|
Poisson Equation |
 |
Smoothing using Curvature Flows |
Mean Curvature Flow (11 iterations) (Updating Laplace Matrix in each iteration Vs using the initial one) Using the initial matrix (only updating mass matrix) helps with avoiding singularities  Stationary-Laplacian Mean Curvature flow (~ 40 iterations, step size 0.001 vs 11 with step size 0.01) step size affects speed of convergance  |
Distance Computation was implemented using the heat method. This is based on a paper by Crane et al. First, the heat equation is solved on the mesh to compute the heat flow. Then, the heat flow is used to compute the distance from a given vertex to all other vertices. This involves normalizing the heat flow and negating it to get a vector field pointing along geodesics. A function whose gradient follows this vector field reproduces the final distance.
| Algorithm | Results |
|---|---|
Geodesics using the Heat Method 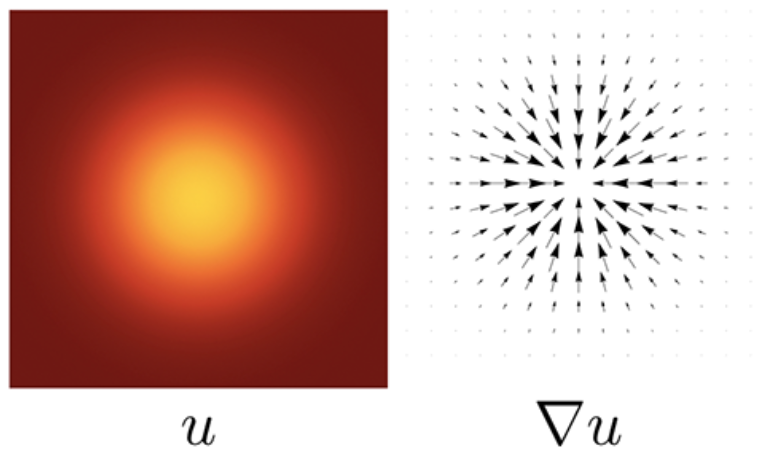 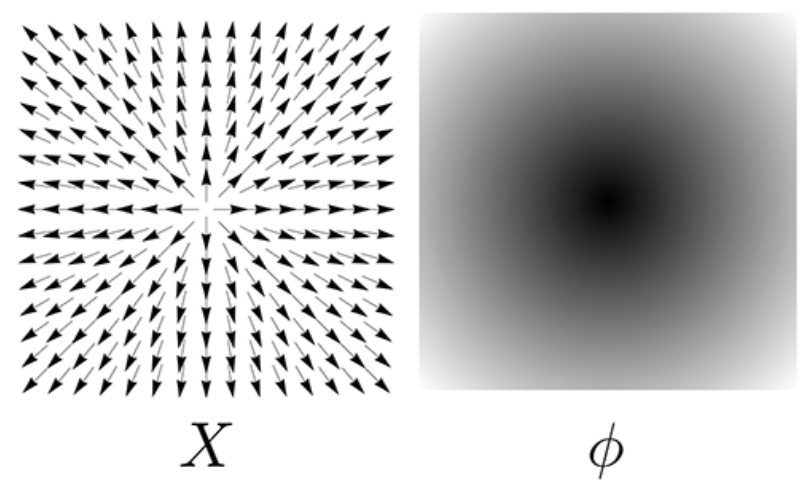 (I) Heat is allowed to diffuse for short time (top-left). (II) The temperature gradient (top-right) is normalized & negated to get a field (bottom-left) pointing along geodesics. (III) A function whose gradient follows the vector field recovers the final distance (bottom-right). |
 |
This is also an application of the laplace-beltrami operator. The Complex Laplacian was used to implement the conformal parameterization of a mesh.
| Algorithm | Results |
|---|---|
Conformal Parameterization |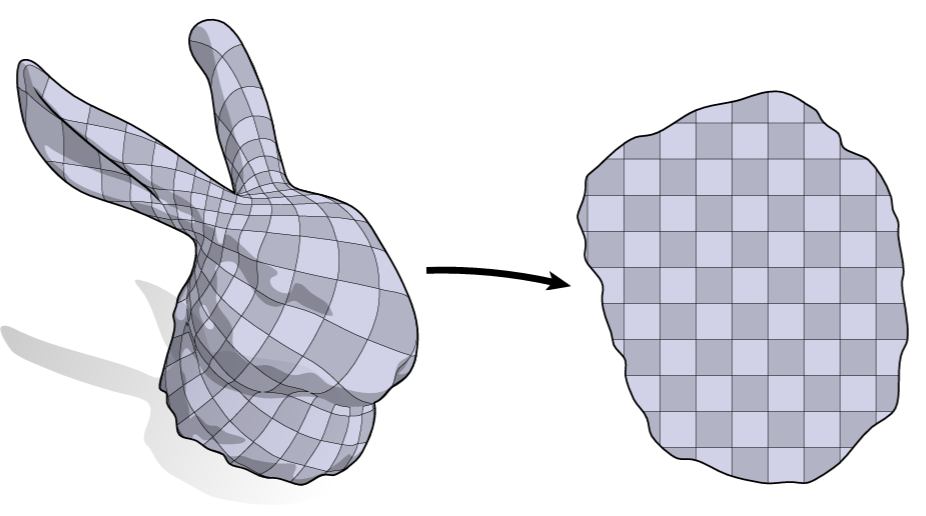
 |
TBA
- Geometry processing and linear algebra - Geometry Central, which in turn has dependencies on Eigen and/or Suitesparse.
- Visualization - Polyscope
- Unit tests - Google Test