gfadini / fast-cma-es

A Python 3 gradient-free optimization library

fcmaes - a Python 3 gradient-free optimization library

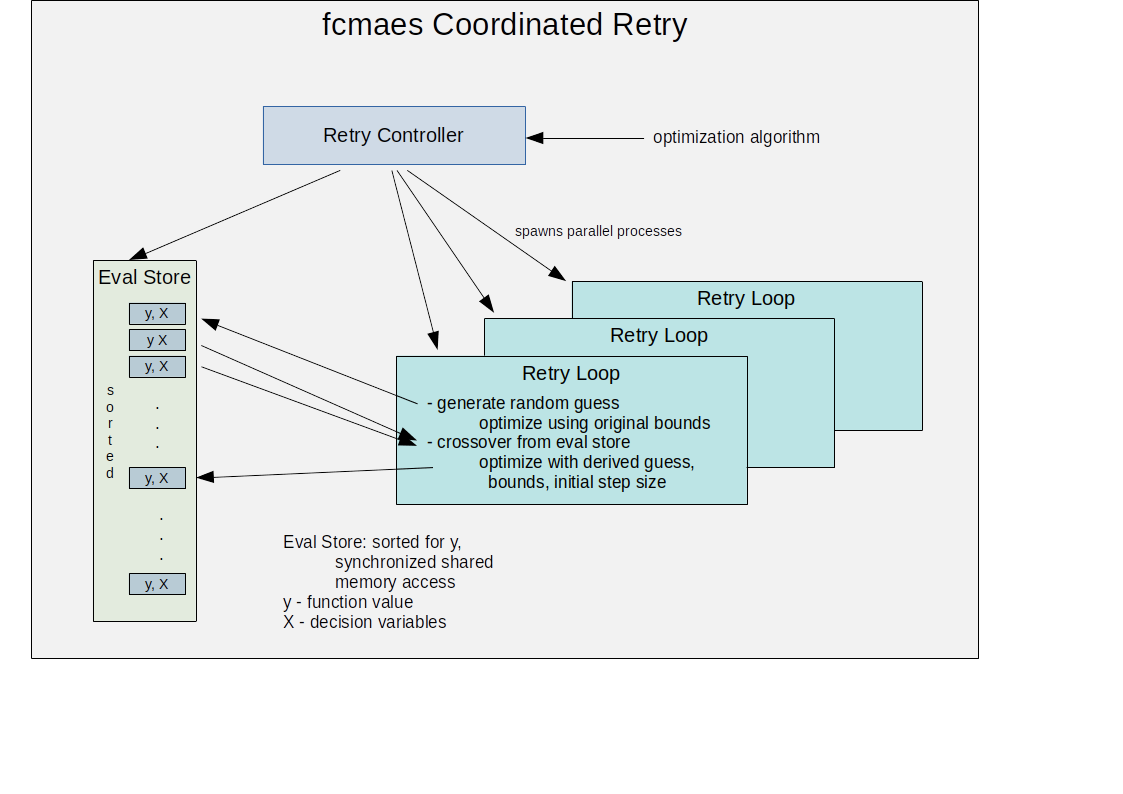
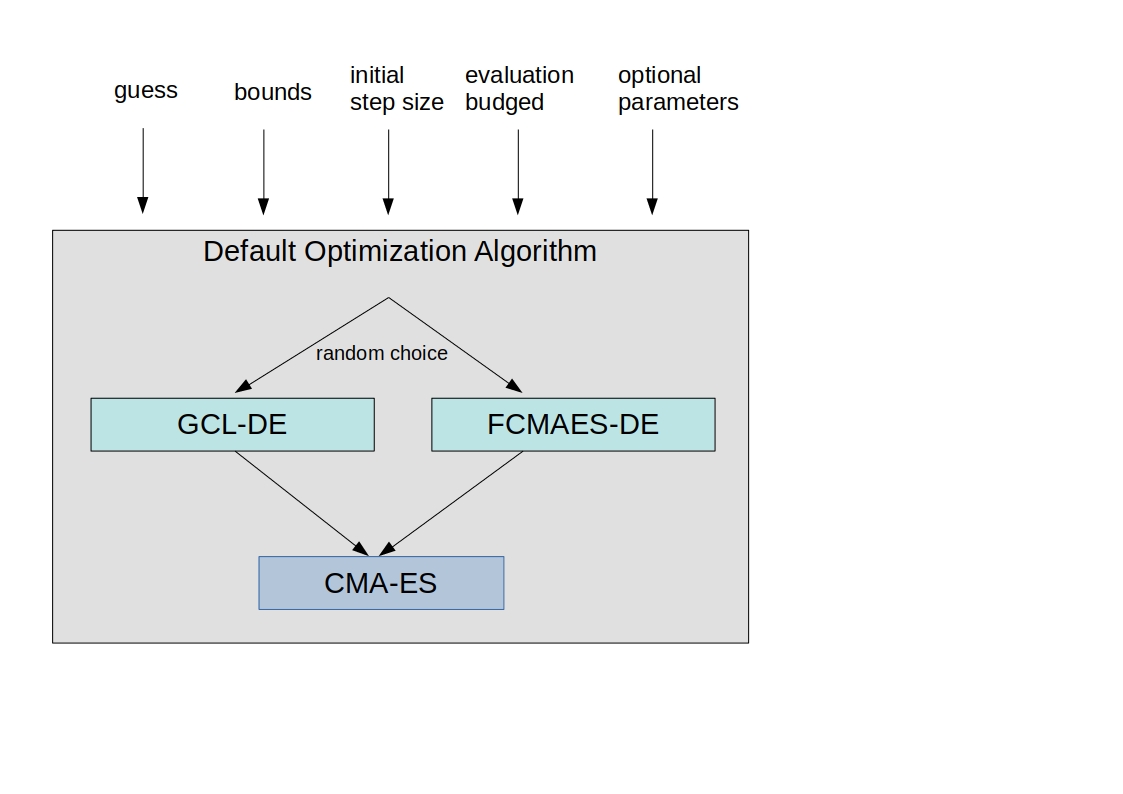
fcmaes complements scipy optimize by providing additional optimization methods, faster C++/Eigen based implementations and a coordinated parallel retry mechanism. It supports the multi threaded application of different gradient free optimization algorithms. The coordinated retry can be viewed as a new meta algorithm operating on a population of user defined optimization runs. Its default optimization algorithm is a sequence of differential evolution and CMA-ES well suited for many ill conditioned, non-continuous objective functions. For optimization on a cluster see fcmaesray, an extension of fcmaes based on ray.

Documentation

Tutorial, Multi-Objective, gbea TopTrumps Benchmark, MO-DE-NSGAII, Pagmo results, Pykep gym results, Constraints, Expressions, ODE, Hyper Parameters . Delayed Update

Features

• fcmaes is focused on optimization problems hard to solve.

• Minimized algorithm overhead - relative to the objective function evaluation time - even for high dimensions.

• Parallel coordinated retry of sequences and random choices of optimization algorithms. See Expressions.

• Parallel objective function evaluation for CMA-ES and Differential Evolution.

• New DE (differential evolution) variant optimized for usage with parallel coordinated retry and the DE→CMA sequence.

• GCL-DE (differential evolution) variant from Mingcheng Zuo.

• BiteOpt algorithm from Aleksey Vaneev.

• Fast C++ implementations of CMA-ES, differential evolution, dual annealing and the Harris hawks algorithm.

• Integrates scipy and NLopt optimization algorithms for use with the coordinated retry.

• Parallel retry for PAGMO2 algorithms and problems.

Performance

In the literature optimization algorithms are often compared by the average result they achieve using a specific number of function evaluations. But in the real world faced with real optimization problems we are usually interested in a different metric: How long does it take to compute a reasonable solution, say not worse than 0.5% above the absolute optimum, with the given hardware. For an optimization library this means: How long does it take to compute a reasonable solution if I choose the best algorithm(s) of the library, optimally configured and optimally parallelized on the given hardware?

fcmaes provides fast parallel example solvers for the real world space flight design problems GTOP and for the F-8_aircraft problem based on differential equations. On GTOPX you can find implementations of the corresponding objective functions using different programming languages. The solution times given in the tables below are for Linux / AMD 5950x CPU.

Table 1. GTOP coordinated retry results for stopVal = 1.005*absolute_best

problem	runs	absolute best	stopVal	success rate	mean time	sdev time
Cassini1	100	4.9307	4.95535	98%	7.43s	10.7s
Cassini2	100	8.383	8.42491	97%	55.18s	39.79s
Gtoc1	100	-1581950	-1574080	100%	25.88s	22.15s
Messenger	100	8.6299	8.67305	100%	18.12s	15.48s
Rosetta	100	1.3433	1.35002	100%	25.05s	10.5s
Tandem EVEES Constrained	100	-1500.46	-1493	68%	519.21s	479.46s
Sagas	100	18.188	18.279	99%	7.59s	6.91s
Messenger Full	100	1.9579	1.96769	41%	3497.25s	2508.88s
Messenger Full	100	1.9579	2.0	59%	1960.68s	2024.24s

Note that 'stopVal' is the threshold value determining success and 'mean time' includes the time for failed runs. Execute benchmark_gtop.py to reproduce these results. The same optimization algorithm was applied for all problems, using the same parameters both for the optimization algorithm and the coordinated retry.

Table 2. GTOP coordinated retry results for reaching the absolute best value

problem	runs	absolute best	stopVal	success rate	mean time	sdev time
Cassini1	100	4.9307	4.93075	98%	8.73s	10.85s
Cassini2	100	8.383	8.38305	44%	310.18s	283.52s
Gtoc1	100	-1581950	-1581949	100%	46.41s	35.57s
Messenger	100	8.6299	8.62995	98%	57.91s	39.97s
Rosetta	100	1.3433	1.34335	27%	268.18s	207.59s
Tandem	100	-1500.46	-1500	65%	564.26s	517.94s
Sagas	100	18.188	18.189	99%	8.76s	7.01s

Optimization algorithms

• CMA-ES: Implemented both in Python and in C++. The Python version is faster than CMA but slower than the C++ variant. The Python variant provides an ask/tell interface and supports parallel function evaluation. Both CMA variants provide less configurability than CMA. The Python implementation supports the ask/tell interface and parallel function evaluation.

• Differential Evolution: Implemented both in Python and in C++. Additional concepts implemented here are temporal locality, stochastic reinitialization of individuals based on their age and oscillating CR/F parameters. The Python implementation supports the ask/tell interface and parallel function evaluation.

• GCL-DE: Eigen based implementation in C++. See "A case learning-based differential evolution algorithm for global optimization of interplanetary trajectory design, Mingcheng Zuo, Guangming Dai, Lei Peng, Maocai Wang, Zhengquan Liu", doi.

• BiteOpt algorithm from Aleksey Vaneev BiteOpt.

• Dual Annealing: Eigen based implementation in C++. Use the scipy implementation if you prefer a pure python variant or need more configuration options.

• Harris' hawks: Eigen based implementation in C++. Use HHO if you prefer a pure python variant. See Harris' hawks optimization: Algorithm and applications Ali Asghar Heidari, Seyedali Mirjalili, Hossam Faris, Ibrahim Aljarah, Majdi Mafarja, Huiling Chen, Future Generation Computer Systems, DOI: https://doi.org/10.1016/j.future.2019.02.028 .

• Expressions: There are two operators for constructing expressions over optimization algorithms: Sequence and random choice. Not only the four algorithms above, but also scipy and NLopt optimization methods and custom algorithms can be used for defining algorithm expressions. Default method for the parallel retry is the sequence (DE | GLC-DE) → CMA with the evaluation budget equally distributed.

Installation

Linux

• pip install fcmaes

Windows

• pip install fcmaes

• install C++ runtime libraries https://support.microsoft.com/en-us/help/2977003/the-latest-supported-visual-c-downloads

Python multiprocessing is currently flawed on Windows. To get optimal scaling from parallel retry and parallel function evaluation use:

• Linux subsystem for Windows:

  • Linux subsystem or

  • Ubuntu subsystem.

The Linux subsystem can read/write NTFS, so you can do your development on a NTFS partition. Just the Python call is routed to Linux.

MacOS

• pip install fcmaes

• For using the C++ optimization algorithms:

  • adapt CMakeLists.txt

  • generate the shared library: cmake . ; make install

Usage

Usage is similar to scipy.optimize.minimize.

For coordinated parallel retry use:

from fcmaes.optimizer import logger
from fcmaes import advretry
ret = advretry.minimize(fun, bounds, logger=logger())

advretry.minimize has many parameters for fine tuning, but in most of the cases the default settings work well.

In tutorial.py and advexamples.py you find examples for the coordinated retry. Parallel retry does not support initial guess x0 and initial step size input_sigma parameters because it uses generated guesses and step size values. The optional logger logs both into a file and to stdout. For easy problems it is sometimes better to use the simple parallel retry:

from fcmaes.optimizer import logger
from fcmaes import retry
ret = retry.minimize(fun, bounds, logger=logger())

The simple retry logs mean and standard deviation of the results, so it can be used to test and compare optimization algorithms:

from fcmaes.optimizer import logger, De_cpp, Cma_cpp, Sequence
ret = retry.minimize(fun, bounds, logger=logger(), optimizer=De_cpp(100000))
ret = retry.minimize(fun, bounds, logger=logger(), optimizer=Cma_cpp(100000))
ret = retry.minimize(fun, bounds, logger=logger(), optimizer=Sequence([De_cpp(50000), Cma_cpp(50000)]))

Here examples.py you find examples for the simple retry.

The single threaded Python CMA-ES implementation is used as follows:

from fcmaes import cmaes
ret = cmaes.minimize(fun, bounds, x0)
print (ret.x, ret.fun, ret.nfev)

If the initial guess x0 is undefined, a feasible uniformly distributed random value is automatically generated. It is recommended to define bounds, since CMA-ES uses them for internal scaling. Additional parameters are:

• popsize (default 31) - Size of the population used. Instead of increasing this parameter for hard problems, it is often better to use parallel retry instead. Reduce popsize for a narrower search if your budget is restricted.

• input_sigma (default 0.3) - The initial step size. Can be defined for each dimension separately. Both parallel retry mechanism set this parameter together with the initial guess automatically.

• workers (default None): int or None. If not workers is None, function evaluation is performed in parallel for the whole population. Useful for costly objective functions but is deactivated for parallel retry.

For the C++ variant use instead:

from fcmaes import cmaescpp
ret = cmaescpp.minimize(fun, bounds, x0)

Alternatively there is an ask/tell interface to interact with CMA-ES:

es = cmaes.Cmaes(bounds, x0)
for i in range(iterNum):
    xs = es.ask()
    ys = [fun(x) for x in xs]
    status = es.tell(ys)
    if status != 0:
        break

Differential evolution (fcmaes.decpp), Dual Annealing (fcmaes.dacpp) and Harris hawks (fcmaes.hhcpp) provide similar interfaces.

from fcmaes import decpp, dacpp, hhcpp
ret = decpp.minimize(fun, bounds)
ret = dacpp.minimize(fun, bounds, x0)
ret = hhcpp.minimize(fun, bounds)

Check the Tutorial for more details.

Log output of the parallel retry

The log output of the parallel retry contains the following rows:

Simple retry

• time (in sec)

• evaluations / sec

• number of retries - optimization runs

• total number of evaluations in all retries

• best value found so far

• mean of the values found by the retries below the defined threshold

• standard deviation of the values found by the retries below the defined threshold

• list of the best 20 function values in the retry store

• best solution (x-vector) found so far

Mean and standard deviation would be misleading when using coordinated retry, because of the retries initiated by crossover. Therefore the rows of the log output differ slightly:

Coordinated retry

• time (in sec)

• evaluations / sec

• number of retries - optimization runs

• total number of evaluations in all retries

• best value found so far

• worst value in the retry store

• number of entries in the retry store

• list of the best 20 function values in the retry store

• best solution (x-vector) found so far

Comparison with PYGMO/Archipelago

There are different ways to enable parallelization and the exchange of information between optimization runs. Two examples are:

• The approach implemented in fcmaes:

  • Topology of the parallelization is hidden from the user. A simple "minimize" call hides the complexity. Parallelism is implemented using multi-processing which scales better than multi-threading with the number of available processor cores.

• The Archipelago approach as implemented in PAGMO2:

  • Topology has to be defined by the user including how nodes/ islands exchange members of their populations. Members of these populations are solution vectors. This approach gives more control to the user but there is no simple default "minimize" call hiding the complexity. As default parallelism is implemented using multi-threading but it is possible to use multi-processing or even distributed CPUs.

  • Exchange of information between parallel PAGMO threads is based on exchanging population members, which doesn’t fit well with CMA-ES which recreates its whole population each generation.

PYGMO/PAGMO has direct support of constraints and multiple objectives. fcmaes supports parallel retry of PYGMO problems and algorithms, see Constraints Tutorial.

Dependencies

Runtime:

• numpy: https://github.com/numpy/numpy

• scipy: https://github.com/scipy/scipy

Compile time (binaries for Linux and Windows are included):

• Eigen https://gitlab.com/libeigen/eigen (version >= 3.9 is required for CMA).

• pcg-cpp: https://github.com/imneme/pcg-cpp - used in all C++ optimization algorithms.

• LBFGSpp: https://github.com/yixuan/LBFGSpp/tree/master/include - used for dual annealing local optimization.

Optional dependencies:

• NLopt: NLopt. Install with 'pip install nlopt'.

• pygmo2: pygmo. Install with 'pip install pygmo'.

Example dependencies:

• pykep: pykep. Install with 'pip install pykep'.

ESAs Messenger-Full Space Trajectory Design Problem

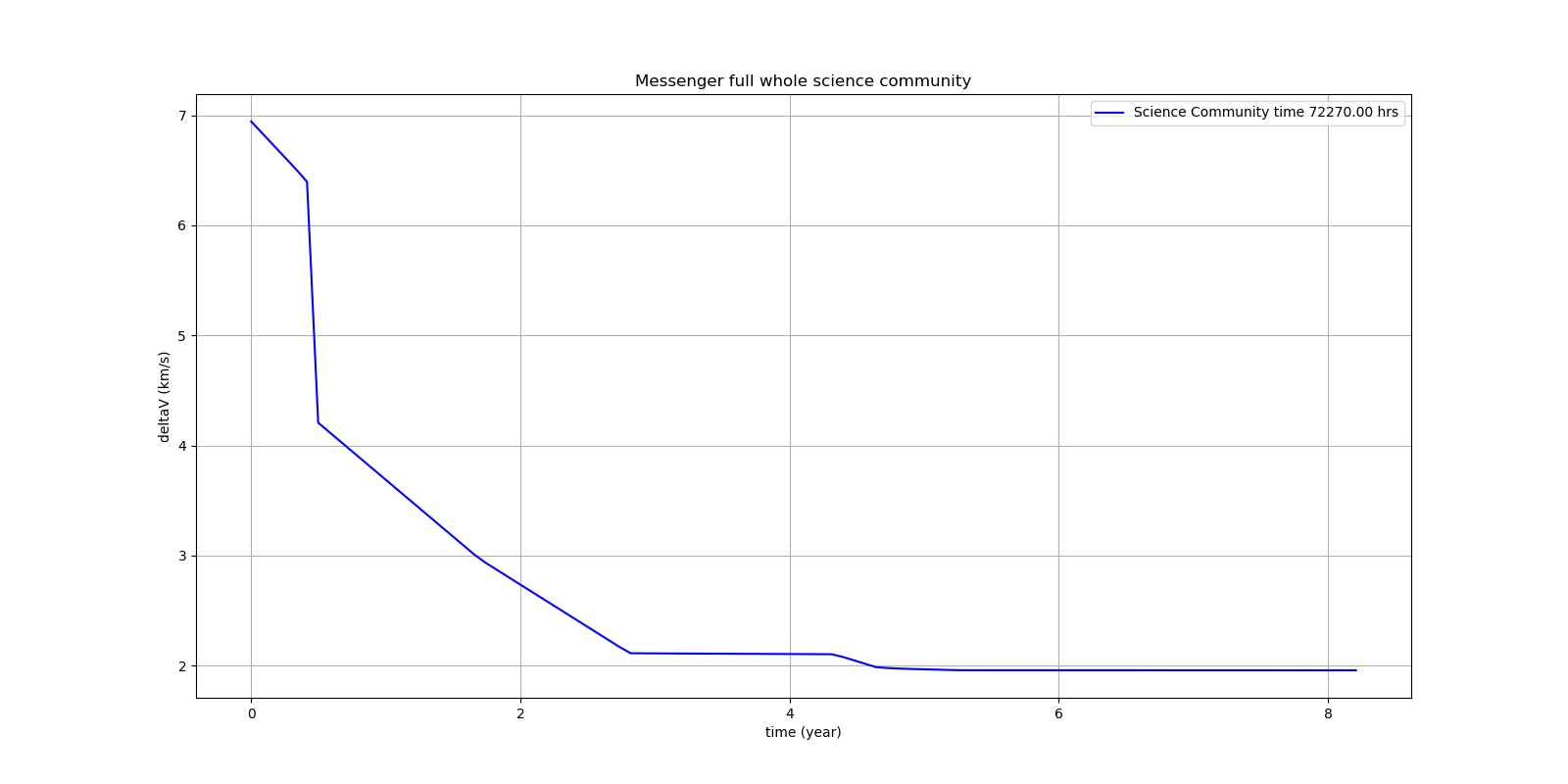
Because of its famous complexity ESAs 26-dimensional Messenger full problem is often referenced in the literature, see for instance MXHCP paper.

fcmaes is the only library capable of solving it using a single CPU: In about 1950 seconds on average using an AMD 5950x (1250 seconds for the java variant) .

The Problem models a multi-gravity assist interplanetary space mission from Earth to Mercury. In 2009 the first good solution (6.9 km/s) was submitted. It took more than five years to reach 1.959 km/s and three more years until 2017 to find the optimum 1.958 km/s. The picture below shows the progress of the whole science community since 2009:

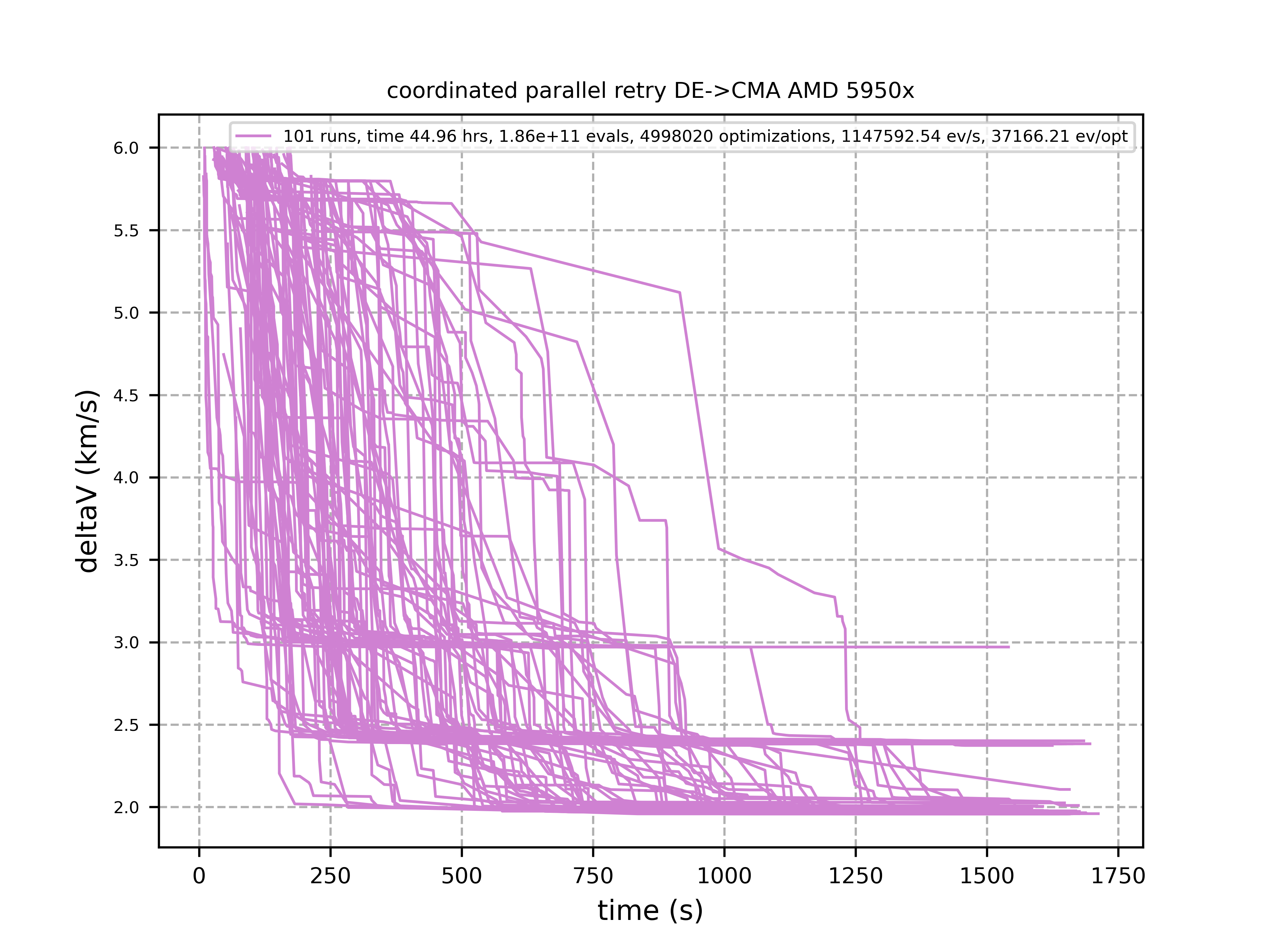
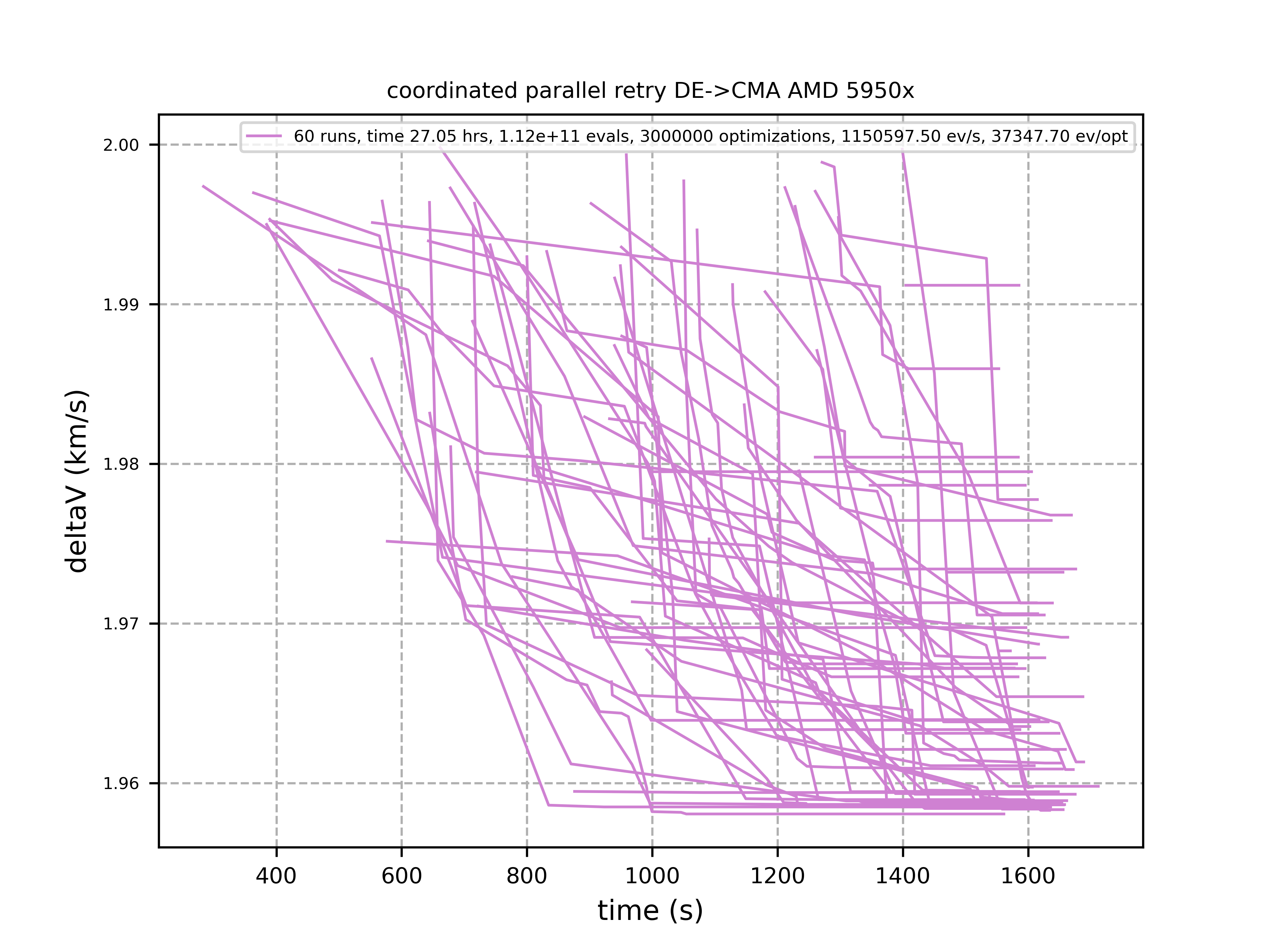
The following picture shows 101 coordinated retry runs:

60 out of these 101 runs produced a result better than 2 km/s:

About 1.2*10^6 function evaluations per second were performed which shows excellent scaling of the algorithm utilizing all 16 cores / 32 threads. https://github.com/dietmarwo/fcmaes-java/blob/master/README.adoc shows that the fcmaes java implementation sharing the same C++ code is significantly faster. fcmaesray shows how a 5 node cluster using 96 CPU-cores executing fcmaes coordinated retry performs in comparison.

Citing

@misc{fcmaes2021,
    author = {Dietmar Wolz},
    title = {fcmaes - A Python-3 derivative-free optimization library},
    note = {Python/C++ source code, with description and examples},
    year = {2021},
    publisher = {GitHub},
    journal = {GitHub repository},
    howpublished = {Available at \url{https://github.com/dietmarwo/fast-cma-es}},
}