Triangle puzzle

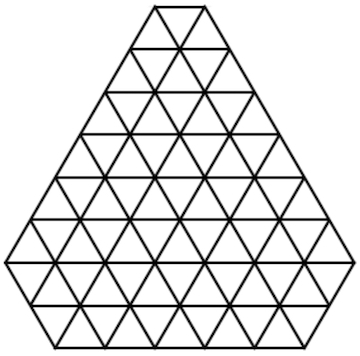
This repository contains the infrastructure I've assembled to document solutions to my triangle puzzle. The goal of the puzzle is to fit the 12 pieces into the given frame. I've called it the triangle puzzle because each piece can be constructed out of 6 equilateral triangles. The individual pieces, and a picture of one example solution, can be found in the assets/ folder.

I've had this puzzle for most of my life, and started informally documenting solutions around 2002. Until September 2018, the same solution had never been discovered twice; there have now been a total of four repeat solutions found. Given that we've discovered over 600 solutions total, I'm curious how many actually exist.

Many solutions have sister solutions reachable by flipping or rotating two or three pieces that form a symmetric shape. I've identified these groups by providing both an ID and a sub-ID for each solution; solutions in a sister group share an ID. There is no formal definition of how major a transformation has to be to qualify as a new solution instead of a sister solution: but ultimately it doesn't really matter if you just want to know how many unique solutions there are. I've generally considered any solution found by looking at an existing solution as a sister solution to that one.

Computational approaches

If you are interested in finding all solutions to this puzzle computationally, feel free to use the resources from this repository. You may also want to check out other projects devoted to solving the puzzle:

solvin-da-puzzle is a theoretically complete project to compute all solutions to this puzzle, but is too inefficient to produce any in practice without choosing a starting point where several pieces have already been placed
TrianglePuzzle is also a theoretically complete project to compute all solutions, but in practice it only produces 723 - too few to plausibly be all of them. We don't know what flaw is causing the project to miss solutions.

I am interested to know how many solutions exist (feel free to contact me for starting ideas if you decide to take this on!), but please do not use this repo as your workspace and please do not flood solutions.csv with computer-generated solutions - I'd like for all solutions recorded there to be discovered manually.

...manual approaches?

If (heaven forbid) you find yourself compelled to solve this puzzle manually without the physical thing at your fingertips, feel free to add your solutions. If you're interested in getting the physical thing at your fingertips, contact me; I have a vague interest in making or ordering 3D printed copies of this puzzle, but have no motivation to do so. You could receive the first prototype!

How solutions are encoded

The key to the encoding of this puzzle is that the frame can be broken down into 72 triangles:

Solutions are recorded as 72-character strings. Each character corresponds to 1 triangle in the frame area. The solution is applied to the frame in rows from left to right: the first three characters correspond to the three triangles in the first row, next five characters to the five triangles in the second row, and so on. The character indicates which puzzle piece is covering that triangle in the solution. Each of the 12 pieces is assigned a character according to the key:

Example solution and corresponding encoding:

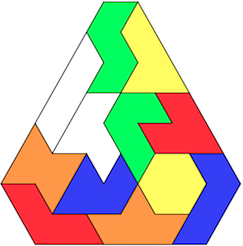
      77b
     977bb
    9977bbb
   993311100
  49333110000
 4444232155588
 6642222a55588
  6666aaaaa88

Adding a solution with Python

While it is possible to enter a solution directly into solutions.csv, it's critical that solutions be entered with Python, both to avoid typos and invalid entries and to ascertain that the solution has not already been discovered.

Dependencies

To use the Python code, you will need matplotlib. The main code is currently in a Jupyter notebook, puzzle.ipynb, but the code in it can be copied into a regular Python file and run from there if preferred. It's written in Python 3, but everything will work in Python 2 if you replace input in the notebook's getSolution() function with raw_input.

Entering your solution

You'll need to fill in the parameters in the notebook with your solution's info. See specific instructions for the parameters in the notebook comments. Once you've filled in the parameters and run the notebook, there are a few options for what the output looks like:

An illustration of the solution you've entered, along with a summary of the other parameters you've entered and an input field with the text "Press enter if good". In this case you have the opportunity to add your solution to the spreadsheet. Please carefully review the illustration and parameters, and if everything looks correct, press enter to submit the solution. Otherwise, type anything in the input field, or just stop the program.
Same as above, except with text "WARNING: Did not pass basic check" and no input field. This means that the program has recognized your solution can't be valid. Please check your solution input and the illustration and try again.
An empty frame and an error message resulting from an invalid parameter. Hopefully those messages should be pretty clear, but if not, let me know by filing an issue - it's possible the parameter verification code has a bug.
(And I can't fully rule out) a stack trace. If this happens, please file an issue with your stack trace and parameters so I can fix it. If you want to debug it yourself, great, but please notify me of the bug. Feel free to do so by putting up a pull request with your fix! ;)

Once you have successfully entered your solution, there are two possible messages you may see. Most likely, your solution will be a new unique solution, and you will get a congratulations message with the ID and sub-ID assigned to it. However, it's also possible that you've found a solution that's already recorded, in which case it will tell you so. PLEASE LET ME KNOW if you independently find a solution that has already been discovered - I'd like to have that information for statistical purposes!

corinaminer / triangle-puzzle