ccj5351 / max_flow

A Small Assignment Code Max-Flow (Ford-Fulkerson’s Algorithm)

1 Problem Definition:

Implement the Ford-Fulkerson flow algorithm using three different methods for finding augmenting paths. Perform a careful experimental comparison of those methods.

2 Method Description:

Here three methods are used to find the augmenting paths for Ford-Fulkerson algorithm. Specifically, the methods include:

• 1. Method 1, BFS traverses the residual capacity graph to find augmenting paths;
• 2. Method 2, DFS traverses the residual capacity graph to find augmenting paths;
• 3. Method 3, BFS traverses the flow graph to find augmenting paths.

3. Experiments:

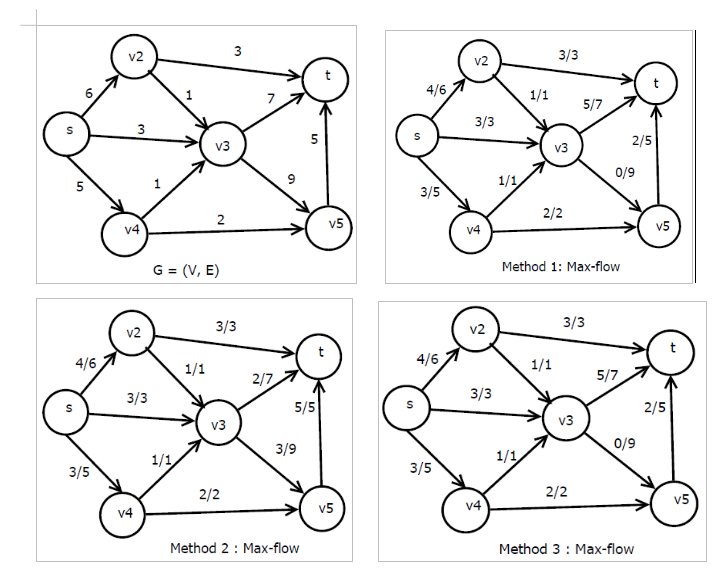
Here the network flow G and the max-flow graphs produced by those methods are shown, where s is the source and t is the sink:

---

Results about the augmenting times for calculating the max-flow:

---

For method 1, that is BFS traverses the residual capacity graph to find augmenting paths, producing 6 augmenting times in total as below:

   Path 1 :  s --> 2 -->  t, path residual capacity = 3;
   Path 2 :  s --> 3 -->  t, path residual capacity = 3;
   Path 3 :  s --> 2 --> 3 -->  t, path residual capacity = 1;
   Path 4 :  s --> 4 --> 3 -->  t, path residual capacity = 1;
   Path 5 :  s --> 4 --> 5 -->  t, path residual capacity = 2;
   Path 6 :  s --> no path -->  t, since path residual capacity = 0;

For method 2, that is DFS traverses the residual capacity graph to find augmenting paths, producing 6 augmenting times in total as below:

   Path 1 :  s --> 2 --> 3 --> 5-->  t, path residual capacity = 1;
   Path 2 :  s --> 2 -->  t, path residual capacity = 3;
   Path 3 :  s --> 3 --> 5 -->  t, path residual capacity = 3;
   Path 4 : s --> 4 --> 3 --> 5 -->  t, path residual capacity = 1;   
   Path 5 :  s --> 4 --> 5 --> 3 -->  t, path residual capacity = 2;
   Path 6 :  s --> no path -->  t, since path residual capacity = 0;

For method 3, that is BFS traverses the flow graph to find augmenting paths, producing 7 augmenting times in total as below:

   Path 1 :  s --> 2 -->  t, path residual capacity = 3;
   Path 2 :  s --> 3 -->  t, path residual capacity = 3;
   Path 3 :  s --> 2 --> 3-->  t, path residual capacity = 1;
   Path 4 :  s --> 4 --> 3 -->  t, path residual capacity = 1;
   Path 5 :  s --> 4 --> 5 -->  t, path residual capacity = 1;
   Path 6 :  s --> 4 --> 5 -->  t, path residual capacity = 1;
   Path 7 :  s --> no path -->  t, since path residual capacity = 0;

4. Conclusion

Even though the augmenting times are the same for method 1 and method 2, DFS searches the residual capacity graph has the most efficient time considering the code implement. And the third method needs more augmenting times to find the max-flow.