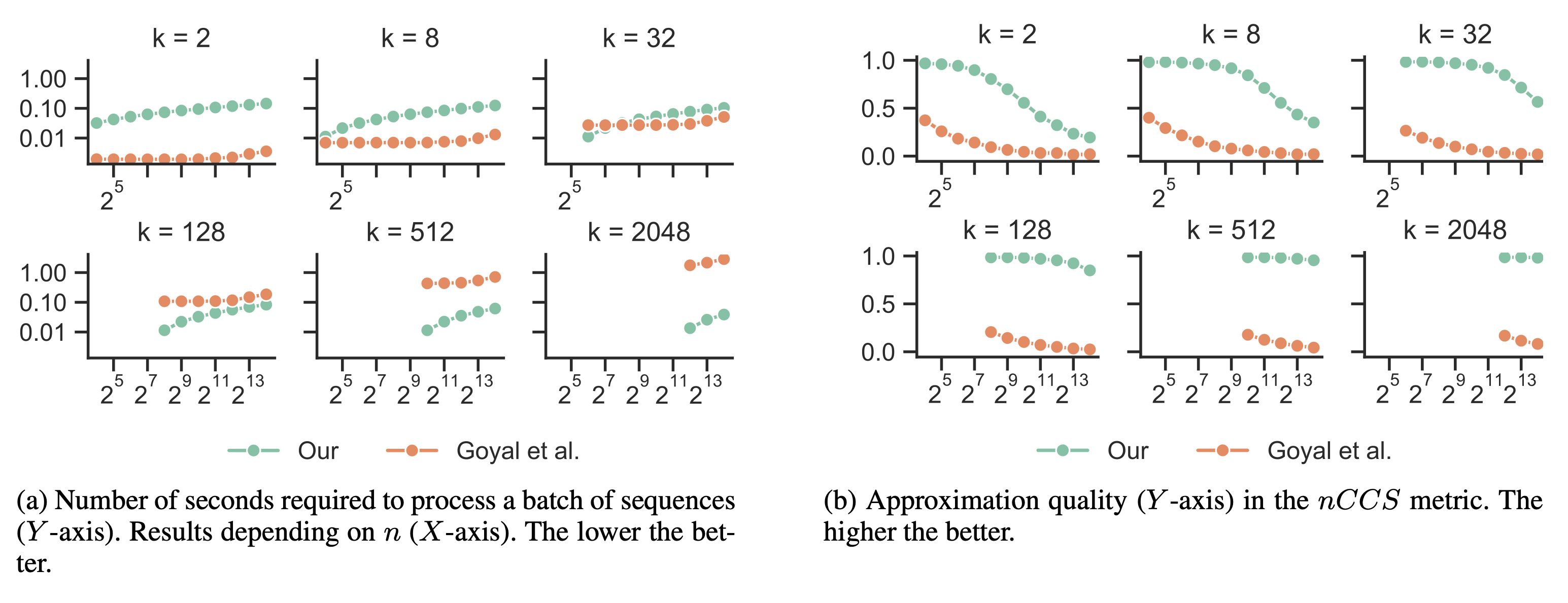
This repository contains a demonstrative implementation of Successive Halving Top-k Operator, complementing the Applica.ai publication, accepted at AAAI'2021. See arXiv, pdf, conference site. Cite us as:
@article{pietruszka2020successive,
title={Successive Halving Top-k Operator},
volume={35},
url={https://ojs.aaai.org/index.php/AAAI/article/view/17931},
number={18},
journal={Proceedings of the AAAI Conference on Artificial Intelligence},
author={Pietruszka, Michał and Borchmann, Łukasz and Graliński, Filip},
year={2021},
month={May},
pages={15869-15870}
}
You can reproduce figures from the paper by:
- Generating files with performance metrics (csv format) with
./benchmarker/benchmark.py. - Making figures from these csv files with
./plotters/make_figures.py.
See provided csv file in ./benchmark_log_16003623822_cuda:0.csv
that will be used by default.
Note: By default, 'cpu' will be used, but 'cuda' version is available in pooler_arena/trainer/benchmark.py.
You may also be interested in using this approach in your code.
The simple guide on using it is below and in ./examples/minimal_example.py.
from topk_arena.models.successive_halving_topk import TopKOperator, TopKConfig
import torch
# Input your settings
k = 256 # your k
n = 8192 # your n
depth = 32 # depth of the representations(vectors, embeddings etc.)
# Build TopK operator and configure it.
topk = TopKOperator()
cfg = TopKConfig(input_len=n,
pooled_len=k,
base=20, # the bigger the better approximation, but can be unstable
)
topk.set_config(cfg)embeddings = torch.rand((1, n, depth)) * 2 - 1
scores = torch.rand((1, n, 1))out_embs, out_scores = topk(embeddings, scores)
out_scores.unsqueeze_(2)We will look at the approximation of the top-1 scoring vector.
top1_hard = embeddings[0, scores.argmax(1).squeeze(), :]
top1_soft = out_embs[0, 0, :]
assert top1_hard.shape == top1_soft.shape
cosine_sim = torch.cosine_similarity(top1_hard, top1_soft, dim=0) # this should be ~1.0
print(f'Approximation quality of Successive Halving TopK for top-1,'
f' as measured by cosine similarity is {cosine_sim.item()}.')The expected output should be something like this:
Approximation quality of Successive Halving TopK for top-1,
as measured by cosine similarity is 0.9996941685676575.
This repository will hopefully solve your problems! :)
Disclaimer: this is not an official Applica.ai product (experimental or otherwise).