Kangonaut / simple-perspective-projection

small project to learn about and experiment with homogeneous coordinates, transformation matrices and perspective projection

Simple Perspective Projection

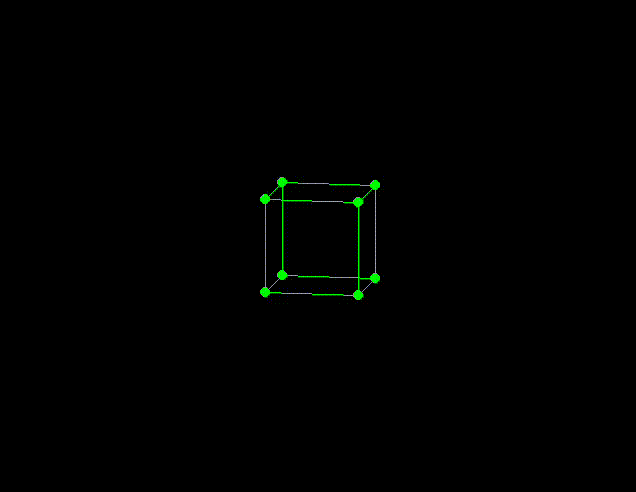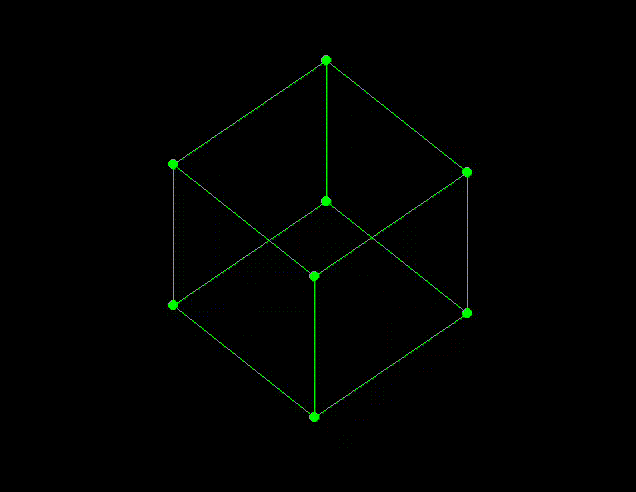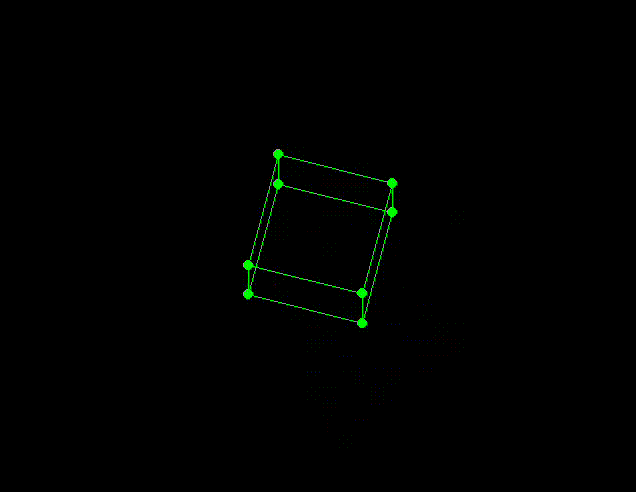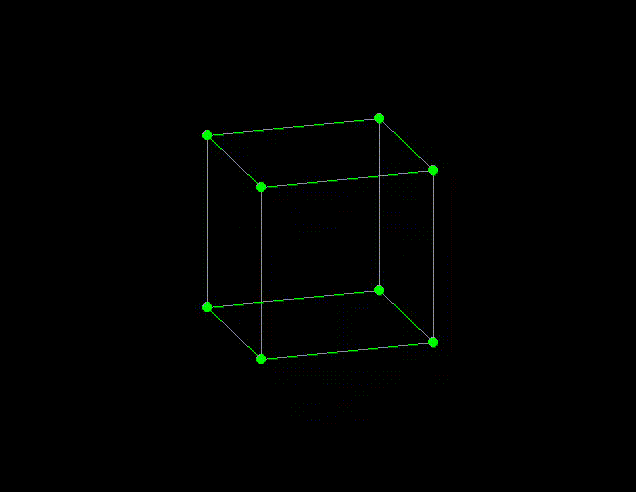
This is a small project I built in order to learn about and experiment with homogeneous coordinates, transformation matrices and perspective projection.

End Result

Perspective Projection

Orthographic Projection

Basic Operations

Scaling

$$ \mathbf{S} = \begin{bmatrix} s_x & 0 & 0 & 0 \\ 0 & s_y & 0 & 0 \\ 0 & 0 & s_z & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ z \\ 1 \\ \end{bmatrix} $$

Rotation

Rotation around the $x$-Axis

• the $x$-coordinate is unchanged and doesn’t influence the result
• the $y$ and $z$ components are projected onto the rotated basis vectors
  • $\mathbf{\hat{i}}$ is simply rotated by $\theta$
  • $\mathbf{\hat{j}}$ can be determined by rotating $\mathbf{\hat{i}}$ by $90°$

$$ \mathbf{\hat{i}} = \begin{bmatrix} cos(\theta) \\ sin(\theta) \end{bmatrix}, \space \mathbf{\hat{j}} = \begin{bmatrix} -sin(\theta) \\ cos(\theta) \end{bmatrix} $$

• thus the resulting rotation matrix is:

$$ \mathbf{R}_x = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & cos(\theta) & -sin(\theta) & 0 \\ 0 & sin(\theta) & cos(\theta) & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \cdot \begin{bmatrix} x \\ \mathbf{y} \\ \mathbf{z} \\ 1 \\ \end{bmatrix} $$

Rotation around the $y$-Axis

$$ \mathbf{R}_y = \begin{bmatrix} cos(\theta) & 0 & -sin(\theta) & 0 \\ 0 & 1 & 0 & 0 \\ sin(\theta) & 0 & cos(\theta) & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \cdot \begin{bmatrix} \mathbf{x} \\ y \\ \mathbf{z} \\ 1 \\ \end{bmatrix} $$

Rotation around the $z$-Axis

$$ \mathbf{R}_y = \begin{bmatrix} cos(\theta) & -sin(\theta) & 0 & 0 \\ sin(\theta) & cos(\theta) & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \cdot \begin{bmatrix} \mathbf{x} \\ \mathbf{y} \\ z \\ 1 \\ \end{bmatrix} $$

Translation

• translation is done by performing a shear transformation in the $4^{th}$ dimension of the homogeneous coordinate system

• to do this, we project our point onto the modified basis vector of the $4^{th}$ dimension

$$ \mathbf{T} = \begin{bmatrix} 1 & 0 & 0 & t_x \\ 0 & 1 & 0 & t_y \\ 0 & 0 & 1 & t_z \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ z \\ \mathbf{1} \\ \end{bmatrix} $$

Projection

Aspect Ratio

• we want to project our points onto our projection window
• the height and the width of the projection window should range from $[-1; +1]$, because this is easier to work with
• for the $y$-axis, we can simply define that our projection window ranges from $-1$ to $+1$
• doing the same for the $x$-axis would not work, since our screen is not necessarily square
• thus we need to introduce an aspect ratio $ar = \frac{w}{h}$
• for the $x$-axis, we now simple define that our projection window ranges from $-ar$ to $+ar$
• by dividing the $x$-values by the aspect ratio, we get our desired range of $[-1; +1]$

Orthographic Projection

• for orthographic projection, we simply ignore the $z$ component
• this means that there is no depth perception
• we simply need to account for the aspect ratio

$$ \mathbf{P_o} = \begin{bmatrix} \frac{1}{ar} & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \cdot \begin{bmatrix} \mathbf{x} \\ y \\ z \\ 1 \\ \end{bmatrix} $$

Perspective Projection

• here we want to introduce depth perception, thus objects farther away should appear smaller
• we first define a field of view $\alpha$ (see Perspective Projection - OGL dev for a visualisation)
• in order to get the projected $y$ component $y_p$, we can use the rule of similar triangles ($z_{near}$ is the distance from the camera to the projection window):

$$ \frac{y_p}{d} = \frac{y}{z} \Rightarrow y_p = \frac{y \cdot z_{near}}{z} $$

• determining $x_p$ works exactly the same, but we have to account for the aspect ratio as well:

$$ x_p = \frac{x \cdot z_{near}}{z \cdot ar} $$

• since the $y$-coordinate of the top of the projection window is 1, we can calculate the distance $z_{near}$ from the camera to the projection window as follows:

$$ tan(\frac{\alpha}{2}) = \frac{\text{opposite}}{\text{adjacent}} = \frac{1}{z_{near}} \Rightarrow z_{near} = \frac{1}{tan(\frac{\alpha}{2})} $$

• putting everything together, we arrive at the following projection matrix:

$$ \mathbf{P_o} = \begin{bmatrix} \frac{z_{near}}{z \cdot ar} & 0 & 0 & 0 \\ 0 & \frac{z_{near}}{z} & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \cdot \begin{bmatrix} \mathbf{x} \\ \mathbf{y} \\ z \\ 1 \\ \end{bmatrix} $$

Resources

• Perspective Projection - OGL dev
• Why do we use 4x4 Matrices in 3D Graphics? - pikuma
• Translation using Shear Transformation - pikuma
• Perspective Projection Matrix - pikuma
• 3D Rendering with Rotation and Projection - The Coding Train