ballistic-motion

This is a Python program to solve an ODE describing a projectile motion in fields of gravity and air resistance. It applies only near Earth's surface at altitudes less than 10 km, distances less than 100 km and speeds much less than the speed of light.

Description

Write Newton's second law:

$$ \sum_{i} \overrightarrow{F_i} = \frac{d \overrightarrow{p}}{dt} \quad (1), $$

where:

$\overrightarrow{F_i}$ - sum of forces acting on a body;
$\overrightarrow{p}$ - momentum of a body.

In this problem sum of forces is combined from the force of gravity ($\overrightarrow{F_g}$) and air resistance (drag) ($\overrightarrow{F_d}$), so to the left we have:

$$ \sum_{i} \overrightarrow{F_i} = \overrightarrow{F_g} + \overrightarrow{F_d}. $$

Rewrite right part assuming constant mass $m$:

$$ \frac{d \overrightarrow{p}}{dt} = \frac{d (m \overrightarrow{v})}{dt} = m \frac{\overrightarrow{v}}{dt}, $$

where $\overrightarrow{v}$ - speed of the body.

Forces are defined as followes:

$$ \overrightarrow{F_g} = m \overrightarrow{g}, $$

$$ \overrightarrow{F_d} = -\frac{1}{2} C_d \rho A \overrightarrow{v^2} = k \overrightarrow{v^2}, $$

where:

$C_d$ - drag coefficient, constant;
$\rho$ - air density , constant;
$A$ - cross sectional area of the body;
$\overrightarrow{v}$ - speed of the body;
$k = -\frac{1}{2} C_d \rho A$.

Substitute forces to (1) and divide both sides by $m$:

$$ \frac{d \overrightarrow{v}}{dt} = \frac{1}{m} \left(\overrightarrow{F_g} + \overrightarrow{F_d} \right) = \frac{1}{m} \left(m \overrightarrow{g} + k \overrightarrow{v^2} \right) $$

Add to the system definition of speed $\overrightarrow{v}$ as the first derivative of displacement $\overrightarrow{s}$:

$$ \left\{ \begin{array}{l} \frac{d \overrightarrow{s}}{dt} & = & \overrightarrow{v} \\ \frac{d \overrightarrow{v}}{dt} & = & \overrightarrow{g} + \frac{k}{m} \overrightarrow{v^2} \end{array} \right. $$

Find projections on the axis (gravity acts only along Oy):

$$ \left\{ \begin{array}{l} \frac{d x}{dt} & = & v_x \\ \frac{d y}{dt} & = & v_y \\ \frac{d v_x}{dt} & = & \frac{k}{m} v_x^2 \\ \frac{d v_x}{dt} & = & -g + \frac{k}{m} v_y^2 \end{array} \right. $$

When given initial values for $x$, $y$, $v_x$, $v_y$ we have initial value problem that can be easily integrated using various numerc algorithms.

Examples

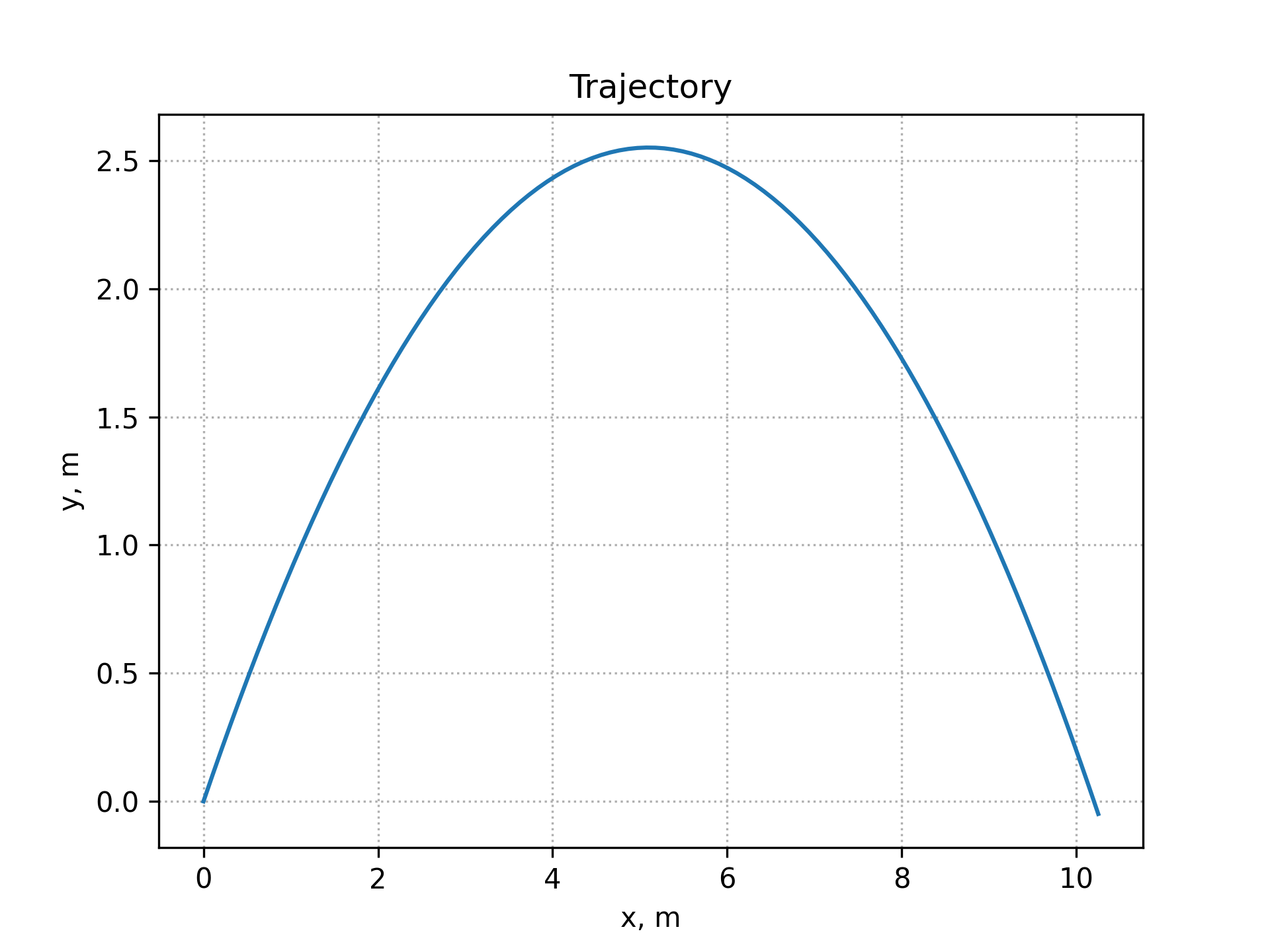
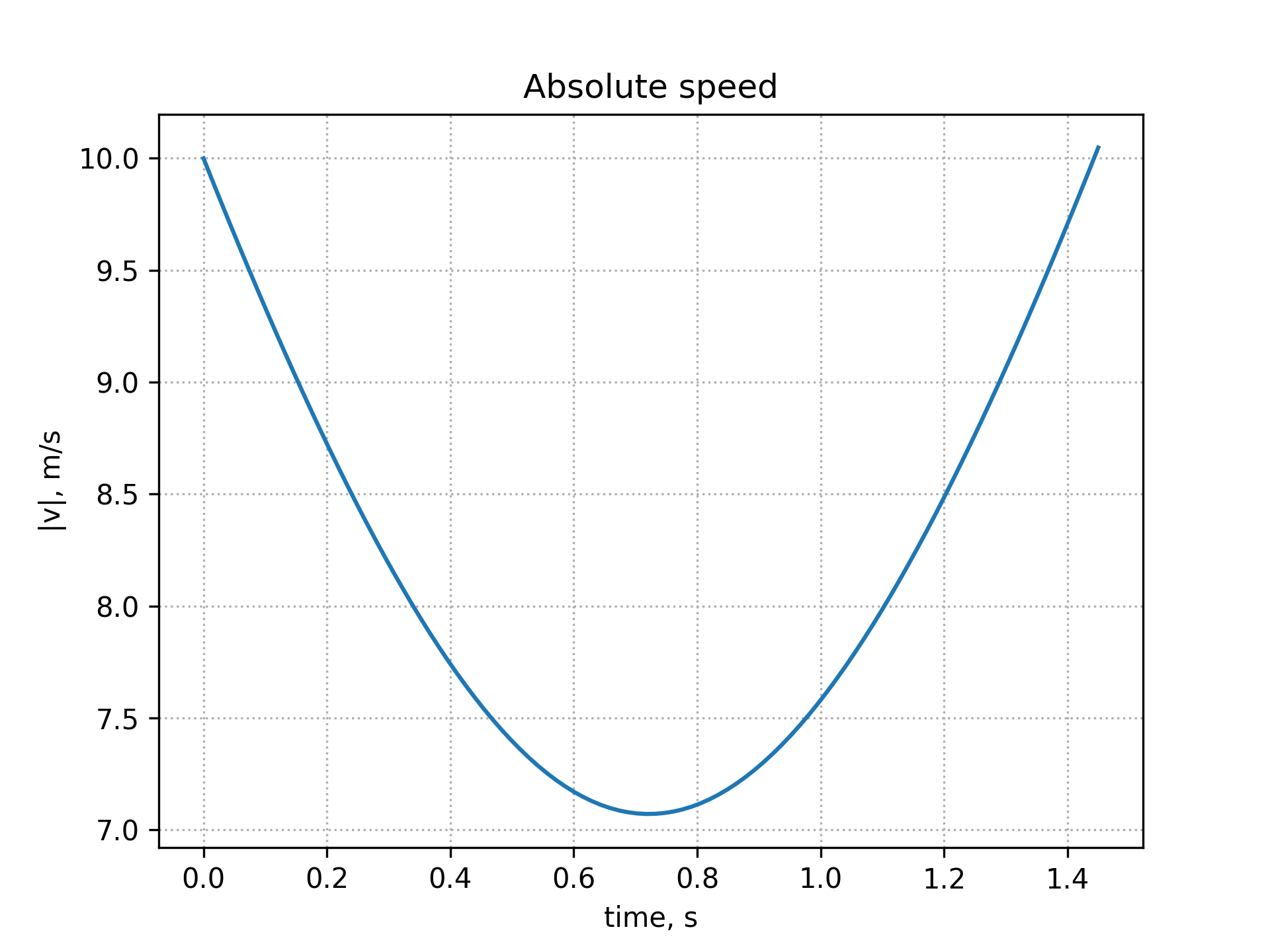
CD = 0, t_max = 1.45, v_0 = 10, angle = 45 degrees

Theoretical values without drag force:

time of flight = $\frac{2 v_0 \sin \theta}{g} \approx \frac{2 \cdot 10 \cdot 0.707}{9.8} = 1.44$ s;
distance at 1.44 s = $\frac{v_0^2}{g} \sin \left( 2 \theta \right) \approx \frac{10^2}{9.8} \cdot 1 = 10.2$ m;
maximum height = $\frac{v_0^2 \sin^2 \theta}{2g} \approx 2.55$ m.

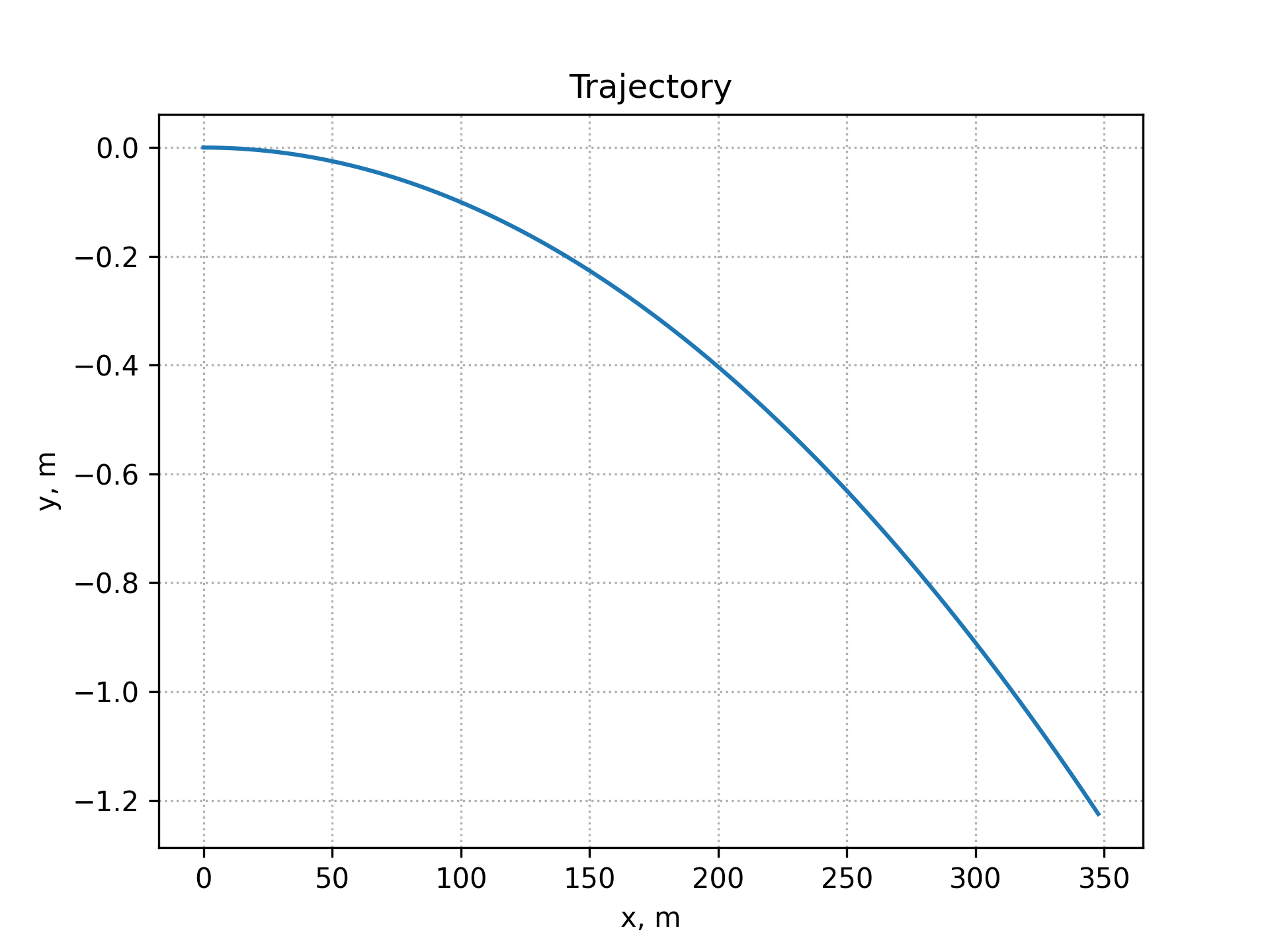
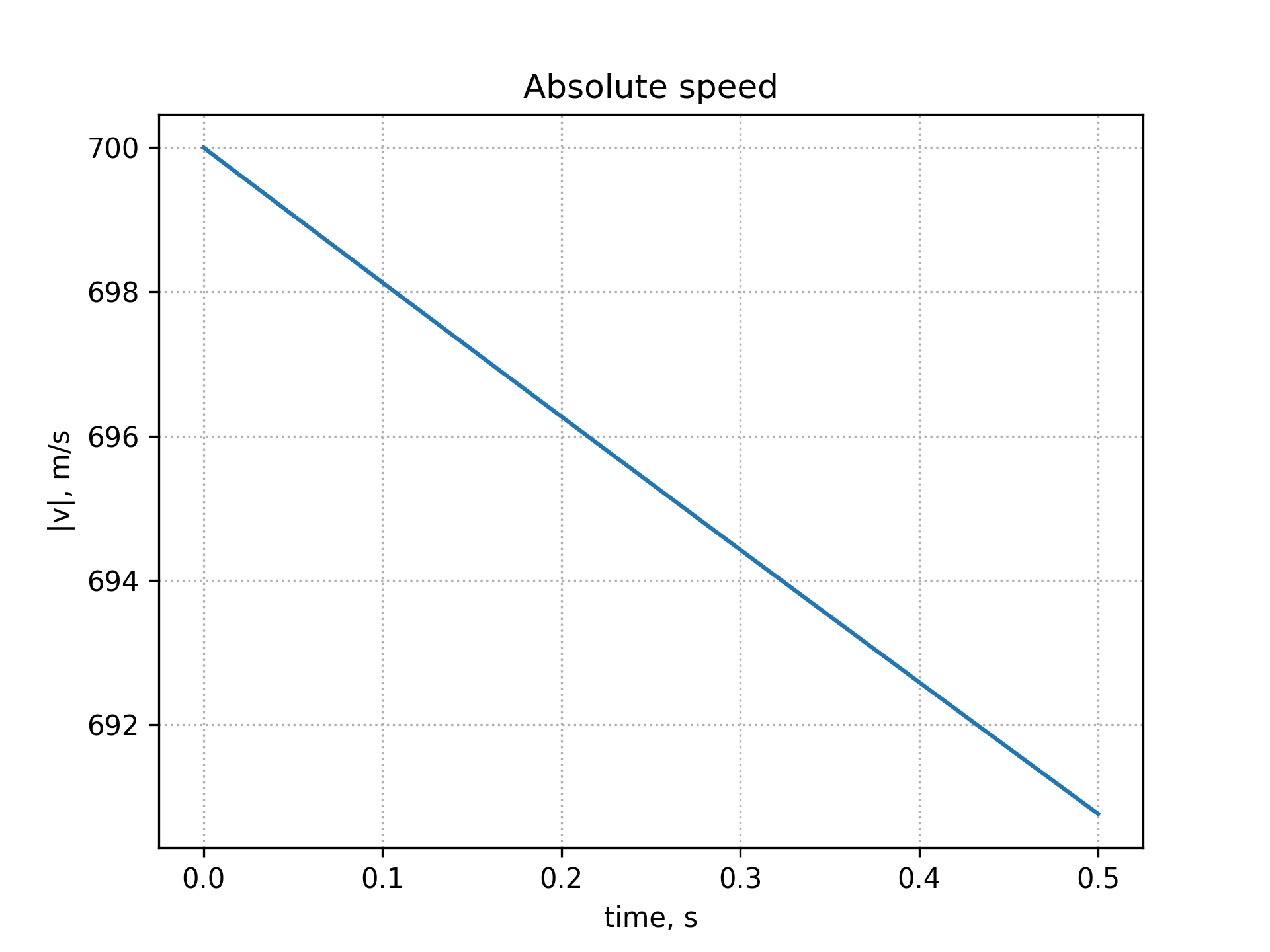
CD = 0.1, t_max = 0.5, v_0 = 700, angle = 0

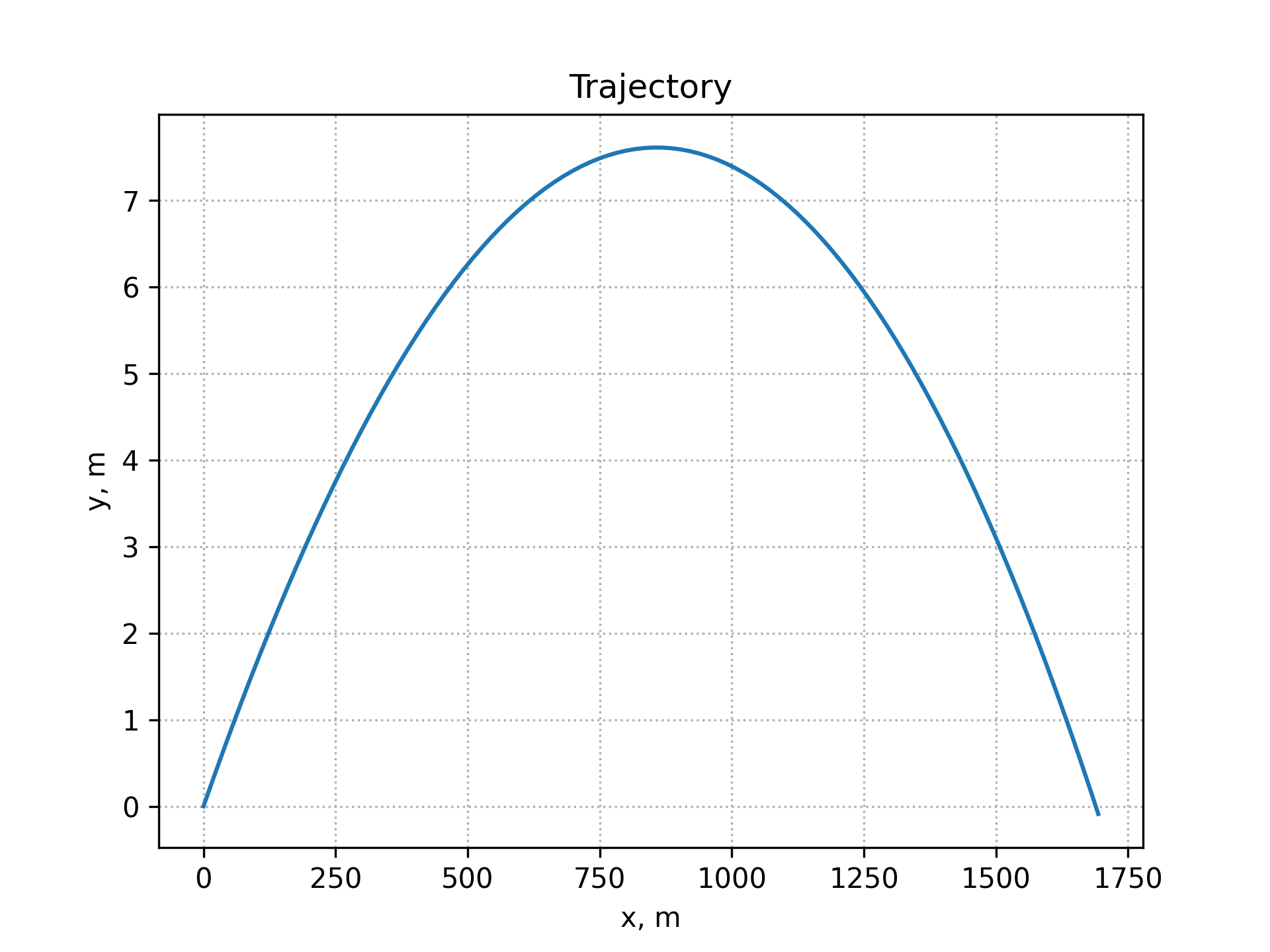
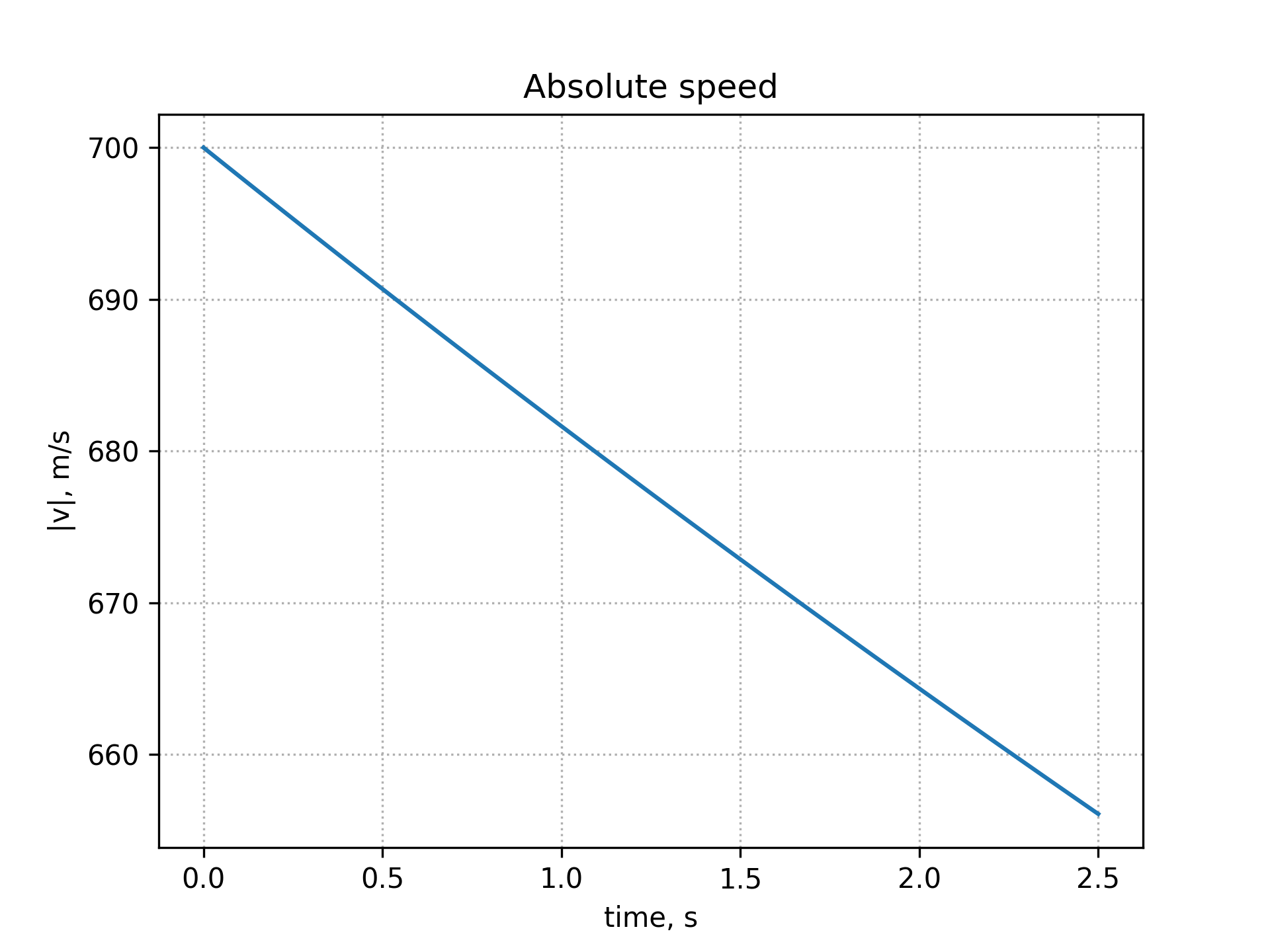
CD = 0.1, t_max = 2.5, v_0 = 700, angle = 1 degree

Theoretical values:

time of flight: 2.49 s;
distance: 1744.97 m;
maximum height: 7.61 m.

vehlwn / ballistic-motion