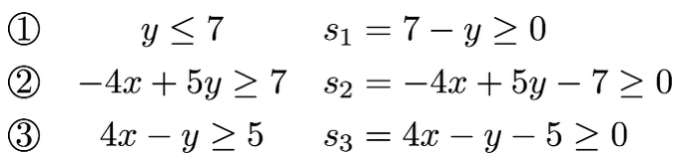tylerneylon / calgebra

Linear algebraic algorithms in C.

calgebra

A C library for linear algebraic optimization problems.

This is a small, fast library focused on solving the following linear problems:

• L²-minimization, aka least squares,
• L¹-minimization,
• L^∞-minimization, and
• general linear programming problems.

These problems and the algorithms used are described in more detail below.

Problem types and algorithms used

L²-minimization

Given input matrix A and column vector b, find column vector x so that:

• Ax=b, and
• ||x||₂ is minimized.

You can solve this in calgebra by using the alg__l2_min function; a usage example is given below.

The algorithm used by calgebra is essentially to project any feasible solution onto the row span of A. Some texts use the term least squares to indicate a slightly different problem, where b may not be in the column span of A, so that the value minimized is ||Ax-b||₂. This is an equivalent problem that can also be solved with alg__l2_min by using input matrix C and column matrix d chosen so that {x: Cx=d} = {Ax-b: x is free}. Internally, calgebra uses a modified Gram-Schmidt QR decomposition to perform the projection onto the row span of A.

L¹-minimization

This is the same as L2-minimization, except that we minimize ||x||₁ instead of ||x||₂.

Specifically, given input matrix A and column vector b, find column vector x so that:

• Ax=b, and
• ||x||₁ is minimized.

You can solve this in calgebra by using the alg__l1_min function; a usage example is given below.

Internally, this problem is reduced to a general linear program, described below.

L^∞-minimization

Given input matrix A and column vector b, find column vector x so that:

• Ax=b, and
• ||x||_∞ is minimized.

As a reminder, for the vector x = (x₁, x₂, .., x_n), the value of ||x||_∞ is simply the maximum |x_i| over all i; that is, it's the maximum absolute value of all the coordinates of x.

You can solve this in calgebra by using the alg__linf_min function; a usage example is given below.

Similar to the L¹ case, this problem is internally reduced to a general linear program, described next.

General linear programming

Given input matrix A and column vectors b and c, find column vector x so that:

• Ax=b,
• x≥0, and
• c^Tx is minimized.

The algorithm used by calgebra is the simplex method, along with Bland's rule to avoid cycling. Although this algorithm is not guaranteed to complete in polynomial time, it is widely believed to be the fastest for most practical applications.

Examples

L¹- and L²-minimization example

In the example below, we call several key functions:

• alg__alloc_matrix(nrows, ncols) allocates and returns a new matrix.
• alg__l{1,2}_min(A, b, x) solves an L{1,2}-minimization problem.
• alg__free_matrix(M) frees matrix M.

A matrix is stored as type alg__Mat, which is a typedef for alg__MatStruct *, defined transparently in the header. Matrices are stored in row-major order, meaning that entries in a single row are stored contiguously in memory.

Use alg__elt(M, i, j) to access the element of matrix M in row i and column j; this is aware of the transposed state of M (that is, the value of M->is_transposed is taken into consideration).

// This problem has the feasible solution set
// (1 1 0) + t(-1 -1 8), where t is free, specified with
// A = (4 4 1)  b = (8)
//     (8 0 1)      (8)
// For this set, x = (1 1 0)^T minimizes ||x||_1.

alg__Mat A = alg__alloc_matrix(2, 3);
alg__set_matrix(A,  4,  4,  1,
                    8,  0,  1 );

alg__Mat b = alg__alloc_matrix(2, 1);
alg__set_matrix(b, 8, 8);
alg__Mat x = alg__alloc_matrix(3, 1);

alg__Status status;

status = alg__l1_min(A, b, x);
if (status == alg__status_ok) {
  // Now x is the solution of the L1-min problem.
}

status = alg__l2_min(A, b, x);
if (status == alg__status_ok) {
  // Now x is the solution of the L2-min problem.
}

alg__free_matrix(x);
alg__free_matrix(b);
alg__free_matrix(A);

The L^∞ case can be handled with the same code, using alg__linf_min in place of alg__l1_min or alg__l2_min.

Linear programming example

This section illustrates use of the alg__run_lp function to solve a linear program.

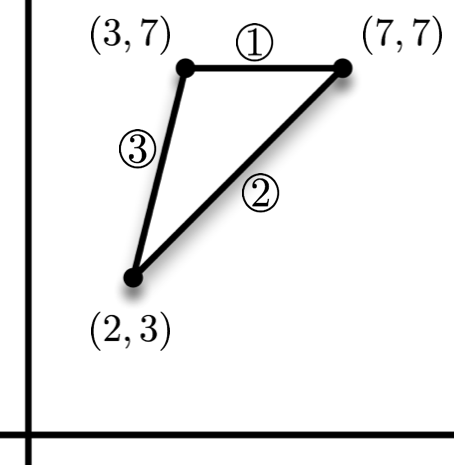
Our goal is to find the point (x, y) in the following triangle which minimizes the value 3x + 2y.

The sides of the triangle have been marked so we can find linear inequalities for each one. A point is in the triangle - boundaries included - if and only if all of the inequalities below are true. To capture this as a standardized linear programming problem, we introduce the slack variables s₁, s₂, and s₃, so that each inequality in x and y alone becomes an equality when paired with a slack variable. The same set of (x, y) points are under consideration, keeping in mind that the slack variables - like all variables in a standard linear programming problem - are constrained to be nonnegative:

We can find the matrices A and b based on the right-hand equalities above. The value of c comes from the coefficients 3 and 2 in the value being minimized, 3x + 2y; since the slack variables are not being minimized, their coefficients in c are all zero.

Here is the code to solve this linear programming problem using lin__run_lp:

alg__Mat A = alg__alloc_matrix(3, 5);
alg__set_matrix(A,  1,  0,  0,  0,  1,
                    0,  1,  0,  4, -5,
                    0,  0,  1, -4,  1 );

alg__Mat b = alg__alloc_matrix(3, 1);
alg__set_matrix(b, 7, -7, -5);

alg__Mat c = alg__alloc_matrix(5, 1);
alg__set_matrix(c, 0, 0, 0, 3, 2);

alg__Mat x = alg__alloc_matrix(5, 1);

alg__Status status = alg__run_lp(A, b, x, c);

if (status == alg__status_ok) {
  // Now x is the solution of the linear program.
}

alg__free_matrix(x);
alg__free_matrix(c);
alg__free_matrix(b);
alg__free_matrix(A);

Values of the alg__Status enum

The following status values are possible:

status value	meaning
alg__status_ok	It's all good.
alg__status_no_soln	Ax=b has no solutions.
alg__status_unbdd_soln	The value of cTx can be made arbitrarily low.
alg__status_input_error	The input matrix dimensions are not as expected, or an input was unexpectedly NULL.
alg__status_lin_dep	(Only from alg__QR) The input had linearly dependent columns; the output is still valid.