tinyHiker / DSA_leetcode

This directory hold my work on data structures and algorithms. It also holds some of my leetcode practice.

Credit to TMU/Ryerson's CPS 305 course for teaching me about data structures and algorithms

Credit to Elshad Kamriov's Udemy Course for teaching me strctures in python https://www.udemy.com/course/data-structures-and-algorithms-bootcamp-in-python/

Overview of Data Structures

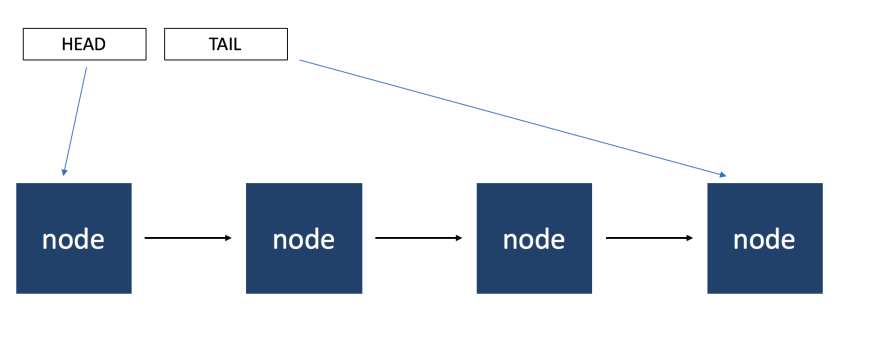
Below -->>

Linked Lists

• Definition: A linear collection of data elements, where each element points to the next, forming a sequence.
• Key Features:
  • Dynamic size.
  • Efficient insertion and deletion.
  • Sequential access (not random).
• Types:
  • Singly linked lists.
  • Doubly linked lists.
• Use Cases: Useful for applications with frequent addition and removal of elements where memory allocation is a concern.

Arrays

• Definition: A collection of items stored at contiguous memory locations.
• Key Features:
  • Fixed size.
  • Elements are of the same type.
  • Random access of elements using indices.
  • Efficient access and iteration.
• Use Cases: When you need fast access to elements using index, and the size of the collection is known and fixed.

Queues

• Definition: A collection of entities that are maintained in a sequence and can be modified by adding at one end (the rear) and removing from the other end (the front).
• Key Features:
  • FIFO (First In, First Out) structure.
  • Enqueue (add) operations at the rear.
  • Dequeue (remove) operations at the front.
• Use Cases: Handling of data where the order of operations is essential, like task scheduling.

Stacks

• Definition: A collection of elements with two main operations: push, which adds to the collection, and pop, which removes the most recently added element.
• Key Features:
  • LIFO (Last In, First Out) structure.
  • Push and pop operations.
• Use Cases: Useful in situations where a reverse order of operations is required, like undo mechanisms in text editors.

Trees

• Definition: A hierarchical data structure with a root value and subtrees of children, each with a parent node.
• Key Features:
  • Non-linear.
  • Each node can have any number of children.
  • Trees are recursive data structures.
• Types:
  • Binary Trees.
  • AVL Trees.
  • Red-Black Trees, etc.
• Use Cases: Representing hierarchical data, like file systems, and for efficient searching and sorting.

Hashmaps (Hash Tables)

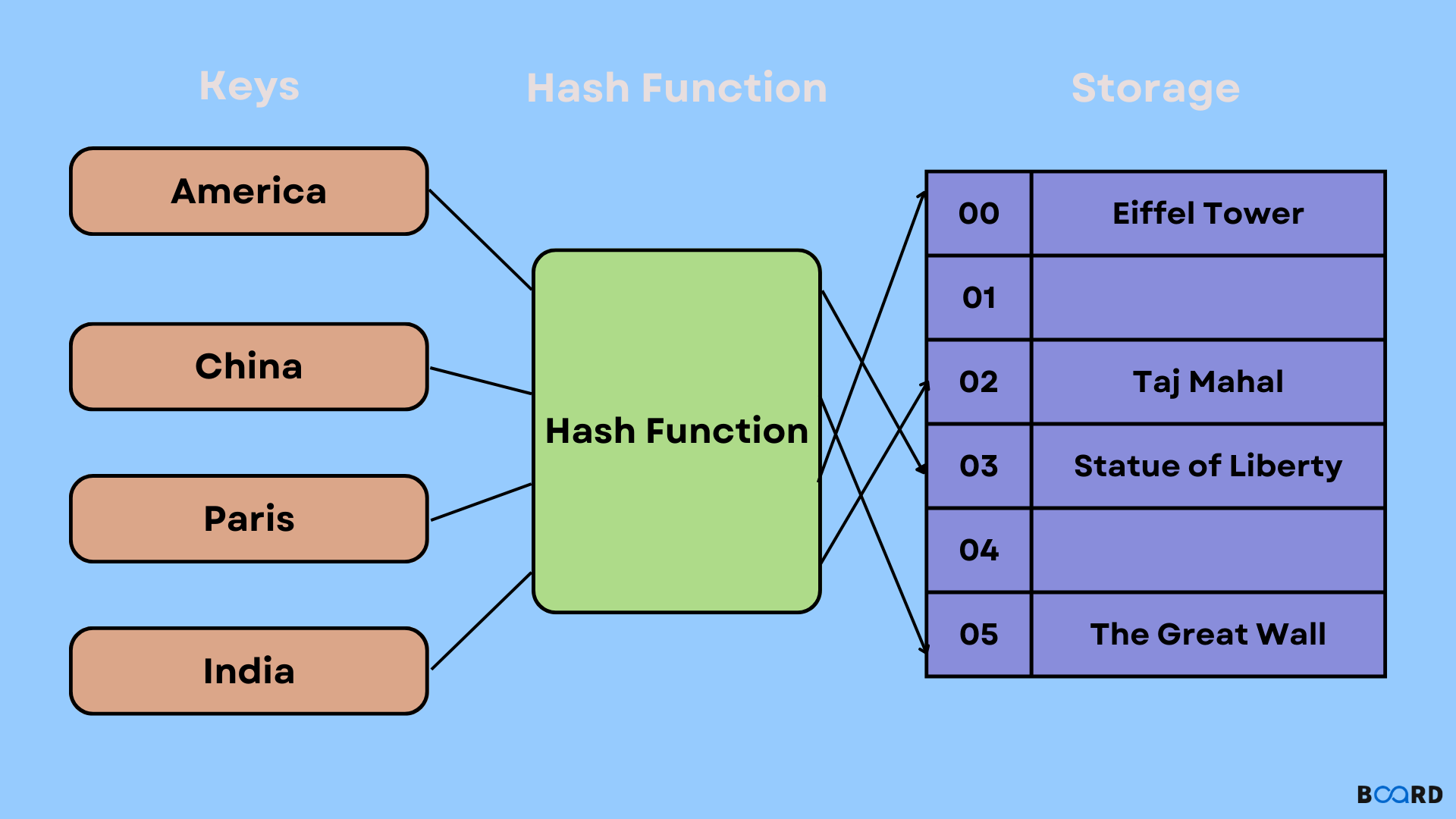
• Definition: A data structure that implements an associative array abstract data type, a structure that can map keys to values.
• Key Features:
  • Key-value pairs.
  • Efficient insertion, deletion, and lookup.
  • Hash function to compute index for a key.
• Use Cases: When you need to access elements by a key, and efficiency is a concern. Common in database indexing.

This summary provides a basic understanding of each data structure, their key characteristics, and typical use cases.

Tree Terminology and Types of Binary Trees

Tree Terminology

• Root: The top node without a parent.
• Edge: A link between a parent and a child node.
• Leaf: A node which does not have children.
• Sibling: Children of the same parent.
• Ancestor: A parent, grandparent, great-grandparent, etc., of a node.
• Depth of a Node: The length of the path from the root to the node, measured in the number of edges.
• Height of a Node: The length of the path from the node to the deepest node connected to it. This length is measured by the number of edges.
• Depth of the Tree: The depth of the root node, which is always zero.
• Height of the Tree: The height of the root node.

Types of Binary Trees

Full Binary Tree

• Each node has either 0 or 2 children. No node has exactly 1 child.

Perfect Binary Tree

• Every node other than leaf nodes has exactly two children.
• All leaf nodes are at the same level.
• The tree has exactly 2^(h+1) - 1 nodes, where h is the height of the tree.
• The number of leaf nodes is (n+1)/2 for a tree with n nodes.

Complete Binary Tree

• Every level, except possibly the last, is completely filled.
• If the last level is not filled, nodes are as far left as possible.

Balanced Binary Tree

• A tree where all leaf nodes are at the same distance from the root.

Deepest Node in a Binary Tree

• The deepest node is the last node reached in a level order traversal.

Tree Search Techniques

Depth First Search (DFS)

1. Preorder Traversal: Visit the root node, then the left subtree, followed by the right subtree.
2. Inorder Traversal: Visit the left subtree, then the root node, and finally the right subtree.
3. Postorder Traversal: Visit the left subtree, the right subtree, and then the root node.

Breadth First Search (BFS)

• Level Order Traversal: Visit each level from left to right.