🤖 Introduction

🤹 PINA is a Python package providing an easy interface to deal with physics-informed neural networks (PINN) for the approximation of (differential, nonlinear, ...) functions. Based on Pytorch, PINA offers a simple and intuitive way to formalize a specific problem and solve it using PINN.

👨‍💻 Formulate your differential problem in few lines of code, just translating the mathematical equations into Python
📄 Training your neural network in order to solve the problem
🚀 Use the model to visualize and analyze the solution!

🤸 Quickstart

Install PINA via PyPI. Python 3 is required:

pip install "pina-mathlab"

🖼️ Solve Your Differential Problem

PINN is a novel approach that involves neural networks to solve supervised learning tasks while respecting any given law of physics described by general nonlinear differential equations. Proposed in Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations, such framework aims to solve problems in a continuous and nonlinear settings.

🔋 1. Formulate the Problem

First step is formalization of the problem in the PINA framework. We take as example here a simple Poisson problem, but PINA is already able to deal with multi-dimensional, parametric, time-dependent problems. Consider:

$$ \begin{cases} \Delta u = \sin(\pi x)\sin(\pi y)\quad& \text{in}, D \\ u = 0& \text{on}, \partial D \end{cases}$$

where $D = [0, 1]^2$ is a square domain, $u$ the unknown field, and $\partial D = \Gamma_1 \cup \Gamma_2 \cup \Gamma_3 \cup \Gamma_4$, where $\Gamma_i$ are the boundaries of the square for $i=1,\cdots,4$. The translation in PINA code becomes a new class containing all the information about the domain, about the conditions and nothing more:

class Poisson(SpatialProblem):
    output_variables = ['u']
    spatial_domain = Span({'x': [0, 1], 'y': [0, 1]})

    def laplace_equation(input_, output_):
        force_term = (torch.sin(input_.extract(['x'])*torch.pi) *
                      torch.sin(input_.extract(['y'])*torch.pi))
        nabla_u = nabla(output_.extract(['u']), input_)
        return nabla_u - force_term

    def nil_dirichlet(input_, output_):
      	value = 0.0
      	return output_.extract(['u']) - value

    conditions = {
        'gamma1': Condition(Span({'x': [-1, 1], 'y':  1}), nil_dirichlet),
        'gamma2': Condition(Span({'x': [-1, 1], 'y': -1}), nil_dirichlet),
        'gamma3': Condition(Span({'x':  1, 'y': [-1, 1]}), nil_dirichlet),
        'gamma4': Condition(Span({'x': -1, 'y': [-1, 1]}), nil_dirichlet),
        'D': Condition(Span({'x': [-1, 1], 'y': [-1, 1]}), laplace_equation),
    }

👨‍🍳 2. Solve the Problem

After defining it, we want of course to solve such a problem. The only things we need is a model, in this case a feed forward network, and some samples of the domain and boundaries, here using a Cartesian grid. In these points we are going to evaluate the residuals, which is nothing but the loss of the network.

poisson_problem = Poisson()

model = FeedForward(layers=[10, 10],
                    output_variables=poisson_problem.output_variables,
                    input_variables=poisson_problem.input_variables)

pinn = PINN(poisson_problem, model, lr=0.003, regularizer=1e-8)
pinn.span_pts(20, 'grid', ['D'])
pinn.span_pts(20, 'grid', ['gamma1', 'gamma2', 'gamma3', 'gamma4'])
pinn.train(1000, 100)

plotter = Plotter()
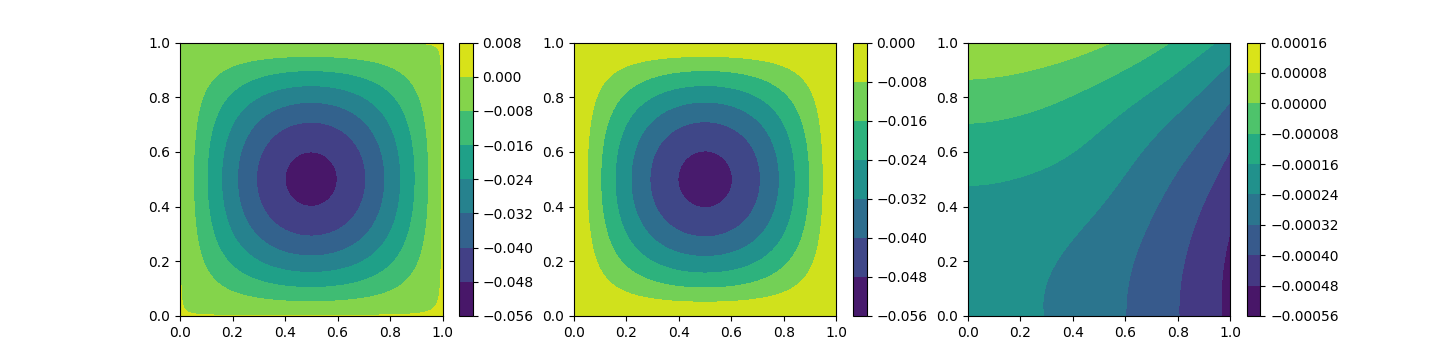
plotter.plot(pinn)

After the training we can infer our model, save it or just plot the PINN approximation. Below the graphical representation of the PINN approximation, the analytical solution of the problem and the absolute error, from left to right.

🙌 Contributing and Community

We would love to develop PINA together with our community! Best way to get started is to select any issue from the good-first-issue label. If you would like to contribute, please review our Contributing Guide for all relevant details.

We warmly thank all the contributors that have supported PINA so far:

Made with contrib.rocks.

📜 License

PINA is distributed under the terms of the MIT License. A complete version of the license is available in the LICENSE.rst file in this repository. Any contribution made to this project will be licensed under the MIT License.

thelearningcurves / PINN_PINA

Solve equations, intuitively.