As part of a new approach to parallelization[4] we need a distributed cache for sparse subsets of extraordinarily large vectors. Imagine that you have a set of really large n-bit vectors, where n > 109. A cache entry consists of some subset of those bits that must take on a particular value, while the rest of the vector can take on any value. Given a vector, we wish to find all cache entries that match. To make this concrete, let's set n = 20 and assume that you have a sequence of 20-bit vectors and I have three cache entries:
Entry 1: bits 1, 3, and 5 must take on the values 101
Entry 2: bits 7,8, and 9 must take on the values 111
Entry 3: bits 1 and 19 must take on the values 01
Then any vector of the form *1*0*1**************
will match entry 1, while any vector of the form
*******111**********
will match entry 2, and any vector of the form:
*0*****************1
will match entry 3. So, the vector 01000100000000000001
matches both entry 1 and entry 3.
Our goal is to design an efficient cache representation
and lookup algorithm that, among other things,
takes advantage of the fact that cache entries 1 and 3
reference the same bit.
Our data sets comprise two files per kernel. Each row of both files[5],[6],[7],[8] is a sequence of plain text, space separated, index-value pairs terminated by a newline character. Each index represents a byte offset into a state vector, so each value is thus between 0 and 255. Taken together, the two files represent the cache and query data recorded while the ASC virtual machine[4] is executing various kernels.
For example, c.dat[5] for the Collatz data set
is a cache
containing 25,643 entries that could achieve superlinear
speed-up of execution of the
Collatz
kernel if only we could query it fast. Each line in c.dat is a
partial state vector that represents up to symmetries
the start state of a completed speculative execution.
Then, q.dat[6] for
the Collatz data set is a recording of the first 1,335,172 queries that
our virtual machine made against c.dat. Each line in q.dat is a
state vector of computation that the virtual machine is sending to the
cache asking for a match.
Each line of both files has the format
key0 value0 ... keyd-1 valued-1,
where d = n/8 is the number of bytes required to represent n
bits. For example, the first line of c.dat is:
20 248 21 255 22 255 23 191 ... 142 119 143 215 276 11 277 0 278 0 279 0
This should be understood as:
For the first cache entry, in order to match against it the incoming state vector must have byte 20 equal to 248, ..., byte 279 equal to 0.
Notice that this first entry is invariant to translations on certain
bytes, e.g. all those indices less than 20, so it doesn't even mention
them. Then, the first line of q.dat is:
0 1 1 0 2 0 3 0 ... 294 0 295 0 296 133 297 31 298 0 299 0
This should be understood as:
For the first state vector, byte 0 has value 1, byte 1 has value 0, byte 2 has value 0, ..., byte 299 has value 0.
The goal of this project is to find an algorithm that constructs
a black box T that minimizes the expected query time of q.dat
against c.dat.
We have a cache c whose entries c(i) are elements of {*,0,1}n, where * is the "don't care" symbol that matches either 0 or 1. We have a query sequence q, whose entries x(i) are elements of {0,1}n.
Our problem is to find a black box T that accepts when an n-bit query vector x(i) "hits" in the cache c, and rejects if x(i) "misses". In both cases, we will require T to provide us with a witness w, where w = (w1, ..., wk) is the length-k sequence of bit indices of x(i) that T examined before deciding. The witness w allows us to locate the matching entry in the hit case and serves as a counterexample in the miss case, but more importantly, allows us to state a strict optimality criterion.
Definition 1 (Strict Optimality) T is strictly optimal for cache c and queries q if its mean witness length <k> = Ex[|w|] is less than or equal to that of all other black boxes.
It seems exceedingly likely that this strict optimum will turn out to be an extremely complicated circuit that will in general take exponential time to find, so we will settle for finding or approximating optimality in the smaller hypothesis class of binary decision trees. Note that binary decision trees are distinct from binary search trees; the latter have more structure in that they impose a total order over node labels.
Problem 1 (Binary Decision Tree) Given a set of n binary tests t = {t(1), ..., t(n)} and a set of m items c = {c(1), ..., c(m)}, output a binary tree where each leaf is labeled with an item from c and each internal node is labeled with a test from t.
The key question is, which binary decision tree? For a cache of size m = |c| there are many decision trees consistent with the statement of Problem 1. Should we assign to the root node the test for the most "contested" bit? If so, under which distribution: that of the cache or that of the queries? What about its left and right children?
We hope to make progress on this question by parametrizing it. That is, we wish to brute force, intellegently find, or obtain oracle access to the parameter a that induces a binary decision tree Ta whose mean witness length <k> = Ex[|w|] is the minimum or approximately the minimum over all binary decision trees.
The purpose
of the oracle described in what follows is to separate our
design problem into
two parts. First, assume that the oracle just hands you the
parameter a. Second,
evaluate the parametrized binary decision tree Ta
using your loss function L(q | a). This loss
function L is a major focus of our work,
since if we get it right, then
we can tell oracle to carry out a search over a; e.g. using
simulated annealing or Nelder–Mead minimization.
Definition 2 (Loss Function) Our loss function L(q | a) = Ex[|w|] is simply the mean number of bits of q accessed during each traversal of Ta induced by queries q.
Our approach arises from a decision-theoretic viewpoint[2], in which one tries to make progress on seemingly fearsome problems by first separating them into two parts: utility, and probability. Often, the problem taken as a whole is extremely difficult to reason about, but after this separation it becomes a somewhat simpler matter of searching for the action a that according to the probability distribution p minimizes one's expected loss (or equivalently, maximizes one's expected utility).
That is, we wish to solve or approximate argamin Ep[L(q | a)]. Currently, we don't have a closed-form solution for p. So in what follows we describe an oracle that (by some means) produces a parameter a, then evaluates the empirical loss of a given query sequence q for a given cache c encoded in the parametrized binary decision tree Ta.
In order to focus on fine-grain details, we will work in this section with a tiny data set that we generate synthetically. First, build the oracle code with optimization level 3:
$ cd cache/oracle
$ make O=3
We generate a simple cache as:
$ echo 1 255 1 248 | rs 2 2 > c.dat
This produces a cache c of size |c| = 2, whose two entries are of the form c(i) = (c0(i), ..., cn-1(i)). In this example, n = 16, and the two entries are c(0) = (*,*,*,*,*,*,*,*,1,1,1,1,1,1,1,1) and c(1) = (*,*,*,*,*,*,*,*,0,0,0,1,1,1,1,1), since we order the bits from least significant to most significant.
We generate a simple query stream as:
$ echo 0 255 1 255 0 0 1 0 | rs 2 4 > q.dat
This produces a query stream q of size |q| = 2, whose two entries are of the form x(i) = (x0(i), ..., xn-1(i)). In this example the two entries are x(0) = (1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1) and x(1) = (0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0).
We now show how to work with each step of the oracle machinery
using the synthetic data set.
The -1 option causes oracle to load the cache into its internal
data structure, then dump that data structure and exit. The following
command should produce no output:
$ diff -u -w <(cat c.dat) <(./oracle -1 -c c.dat)
The oracle assigns a raw code to each cache entry c(i) as it scans it. When it encounters a bit j that is not a "don't care" bit, it extends the raw code for the current cache entry with the new bit index j, using the sign of the index to encode cj(i) = 1 with the symbol -j and cj(i) = 0 with the symbol +j. It uses the "polar map" j(-1)cj(i) to accomplish this encoding.
The -2 option causes oracle to load
the cache, assign the raw code, dump the raw code, then exit. The reader can
verify the encoding of cache entries c(0) and
c(1) from above as follows:
$ ./oracle -2 -c c.dat
-8 -9 -10 -11 -12 -13 -14 -15
+8 +9 +10 -11 -12 -13 -14 -15
The oracle assigns a symbol code to each cache entry by permuting each
raw code in such a way as to result in a valid binary decision
tree. The -3 option causes oracle to dump its symbol codes and exit:
$ ./oracle -3 -c c.dat
-15 -8 -13 -11 -14 -9 -10 -12
-15 +8 +9 -12 -13 +10 -14 -11
The -4 option causes oracle to emit its symbol codes in the GraphViz
language appropriate for dot:
$ ./oracle -4 -c c.dat > c.dot
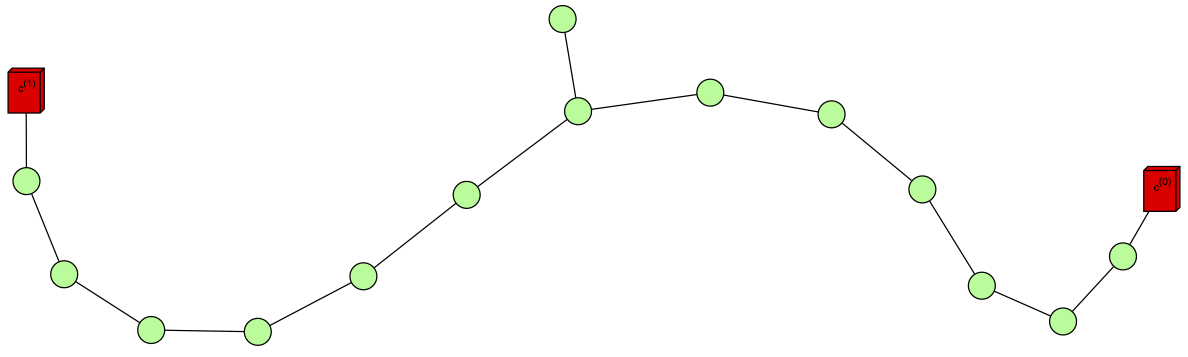
$ dot c.dot -T svg -o c.svg
The resultant plot for our example is:
When we have many cache entries of high dimension, the dot layout
engine is simply
not appropriate and we need to use the fdp layout engine instead,
foregoing most labels.
The -5 option causes oracle to emit its symbol codes in the GraphViz
language appropriate for fdp:
$ ./oracle -5 -c c.dat > c.dot
$ sfdp -Goverlap_scaling=-9 c.dot -T svg -o c.svg
The resultant plot for our example is:
The -6 option causes oracle to load the queries into its internal
data structure, then dump that data structure and exit. The following
command should produce no output:
$ diff -u -w <(cat q.dat) <(./oracle -6 -q q.dat)
We now show how to measure performance of the oracle
binary decision tree on the collatz data set. First,
fetch the data set:
$ wget http://silicoinformatics.seas.harvard.edu/kernels/004.collatz/tiny/collatz.901.c.dat.gz -O c.dat.gz
$ wget http://silicoinformatics.seas.harvard.edu/kernels/004.collatz/tiny/collatz.901.q.dat.gz -O q.dat.gz
Next, extract a sub-sample of the full data sets:
$ zcat c.dat.gz | head -n 128 > c.dat
$ zcat q.dat.gz | head -n 1024 > q.dat
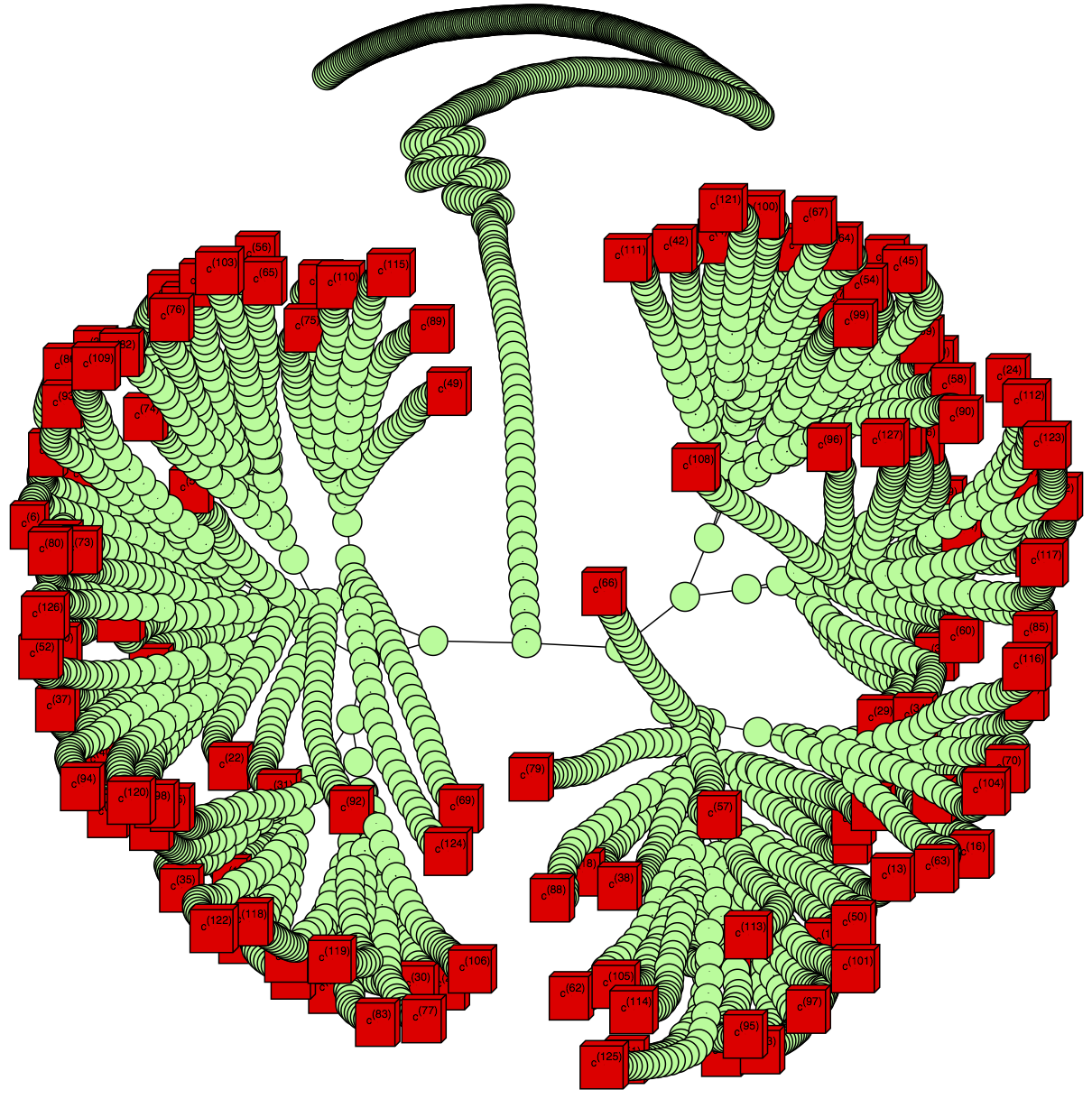
Next, visualize the binary decision tree that the oracle assigns (this is currently just the identity code):
$ ./oracle -5 -c c.dat > c.dot
$ sfdp -Goverlap_scaling=-9 c.dot -T svg -o c.svg
The binary decision tree that results is:
In the following, we first measure the performance
of the binary decision tree implementation,
then we add the -r option
to time the same data set against the reference
linked list implementation:
$ ./oracle -c c.dat -q q.dat > o.dat
$ ./oracle -r -c c.dat -q q.dat > r.dat
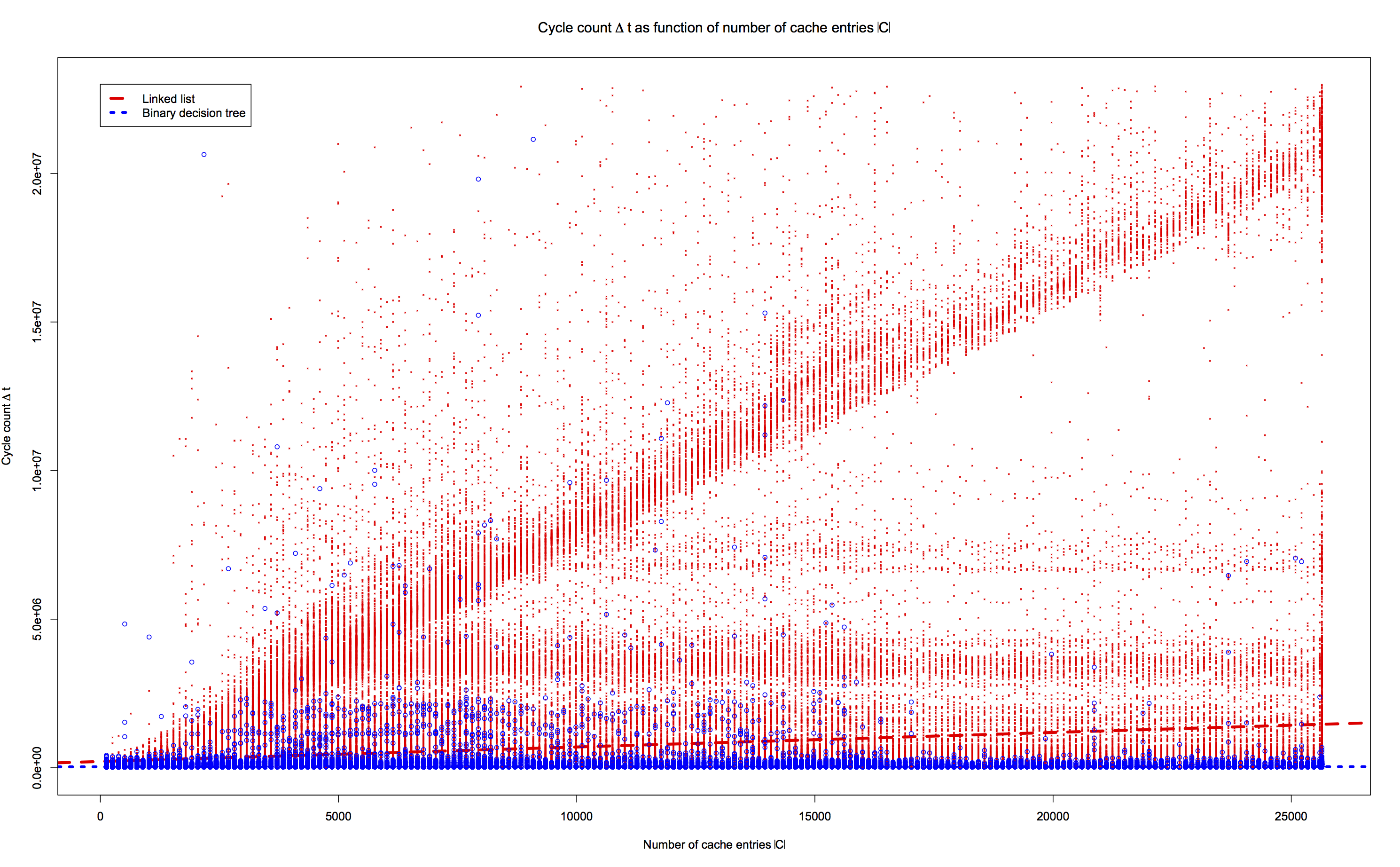
Doing the above repeatedly and with different cache sizes results in the following performance figure:
In the preceding figure, the two dashed lines are
least-squares linear regressions. It is clear
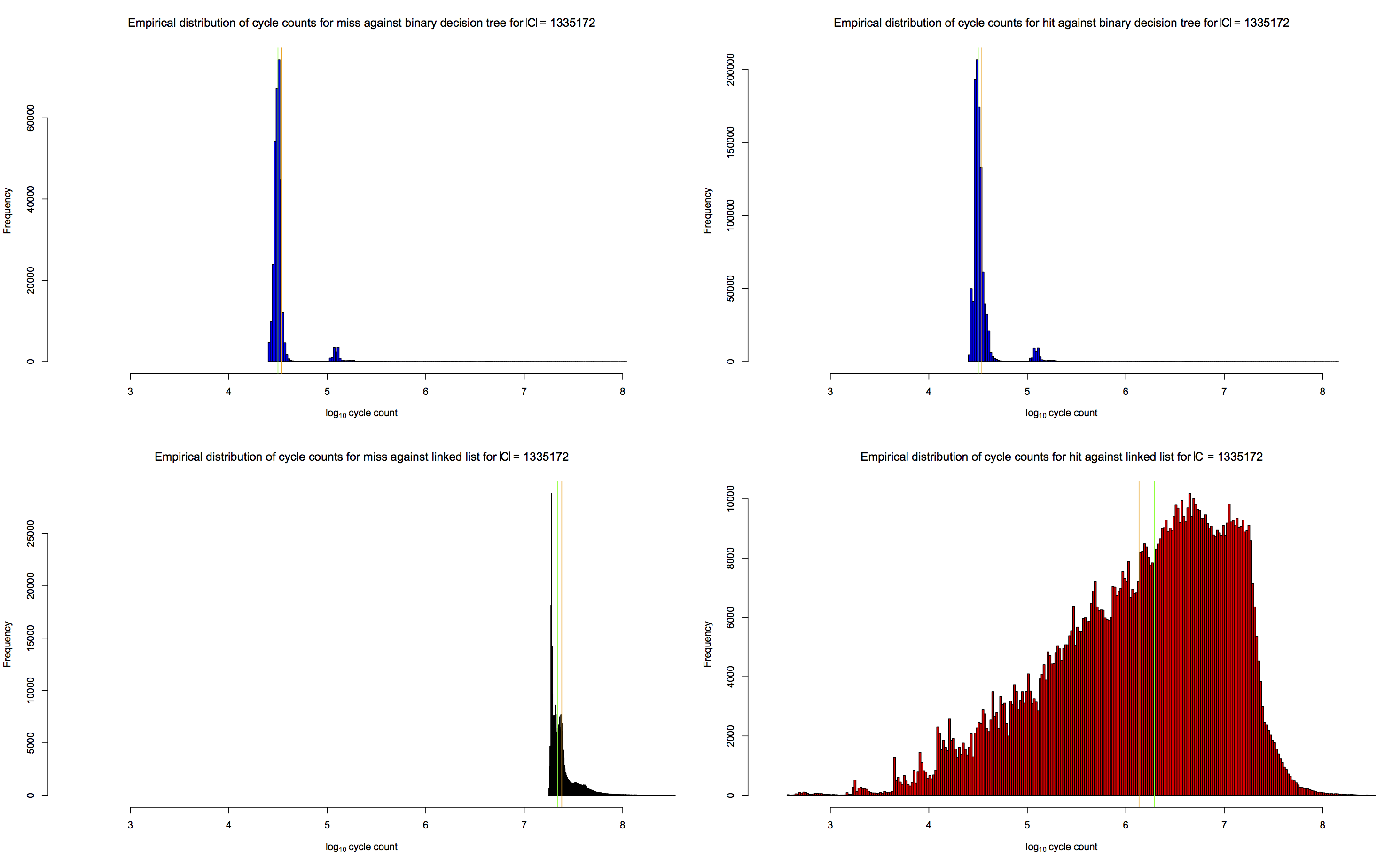
that the binary decision tree scales much better
than the linked list. This is made even more
evident in the following figure, which shows
the performance characteristics of the two
implementations on the full collatz data set
of cache size |C| = 1,335,172:
In arch/cycle_timing.c is our cycle counting logic. Note that we are careful to use execution barriers.
We wrote arch/cycle_timing.c that way because the
Intel manual states that we has to "calibrate" rdtsc in two
ways. First, we have to execute it enough times to settle into
a "steady state", and we have to estimate the minimum overhead imposed
by the two cpuid serializing instructions and the two rdtsc
instructions and the register copies, so we can subtract all
that off our measurements. We imagine that you'd want to do
these two things in one calibration function that you call when
your program starts, where the calibration function returns
the minimum overhead.
See the following figure for what this looks like on one of our server class machines for which the "steady state overhead" is about 290 cycles.
The (probability-weighted) Optimal Binary Search Tree (OBST)[1] admits a dynamic programming solution that exploits both the cache contents and the query distribution. However, it seems impossible to define a total order on our cache entries.
Obviously we want to match state vectors instead of molecules, but the work by Piponi[3] is key because it puts our problem in the nice framework of group theory: a symmetry of a cache entry is an operation to its start state that leaves it invariant. In our case of reads before writes, the symmetries are any operation to the "don't care" bits.
We may find that a BDD library such as BuDDy[14] or CUDD[13] is fast enough to use instead of our own decision tree. This would bring with it a great many algebraic advantages.
If it is prohibitively expensive to calculate the marginal probabilities for each bit, we can employ a count-min sketch[15],[16] to ensure that we get the "heavy-hitters".
If we have the marginal probabilities, we can use them to integrate over any bits we are not conditioning on as we walk the binary decision tree by filling in the missing data we need to input to a logistic regressor with the mean values.
Putting 6.4 and 6.5 together, it may be the case that we can reduce our problem to Hufmann Coding.
Our problem bears some relation to that of IP address routing[17]. See also PATRICIA tries.
DJB makes strong arguments for crit-bit trees as a fundamental data structure, above hash tables[19].
Distribution-aware compressed full-text indexes[18] may be relevant.
Judy arrays[20] appear to have something in common with 256-ary trees.
The authors[21] are saying the right words:
A third class of data structures, known as trie, radix tree, prefix tree, and digital search tree ...
Ideally we would be able to implement this as a single mmap-able file[22].
[1] Optimal Binary Search Trees [1]: http://alg12.wikischolars.columbia.edu/file/view/OPTIMALBST.pdf
[2] Information Theory, Inference, and Learning Algorithms [2]: http://www.inference.phy.cam.ac.uk/itprnn/book.pdf
[3] Hashing Molecules [3]: http://blog.sigfpe.com/2009/06/hashing-molecules.html
[4] ASC: Automatically Scalable Computation [4]: http://people.seas.harvard.edu/~apw/papers/asplos2014_r-paper289.pdf
[5] Collatz cache data set
[5]: http://silicoinformatics.seas.harvard.edu/kernels/004.collatz/tiny/collatz.901.c.dat.gz
[6] Collatz query data set
[6]: http://silicoinformatics.seas.harvard.edu/kernels/004.collatz/tiny/collatz.901.q.dat.gz
[7] Ising cache data set
[7]: http://silicoinformatics.seas.harvard.edu/kernels/007.ising/medium/c.dat.gz
[8] Ising query data set
[8]: http://silicoinformatics.seas.harvard.edu/kernels/007.ising/medium/q.dat.gz
[9] Constructing Optimal Binary Decision Trees is NP-Complete [9]: http://barbra-coco.dyndns.org/eiyou/data/NPComplete.pdf
[10] Approximating Optimal Binary Decision Trees [10]: http://cs.williams.edu/~heeringa/publications/approx2008.pdf
[11] Constrained Binary Identification Problem [11]: http://infoscience.epfl.ch/record/183435/files/STACS2013_app.pdf
[12] Analysis of Algorithms: Trees [12]: http://aofa.cs.princeton.edu/lectures/lectures13/AA06-Trees.pdf
[13] CUDD: CU Decision Diagram Package [13]: http://vlsi.colorado.edu/~fabio/CUDD/
[14] BuDDy - A Binary Decision Diagram Package [14]: http://vlsicad.eecs.umich.edu/BK/Slots/cache/www.itu.dk/research/buddy/
[15] Approximating Data with the Count-Min Data Structure [15]: http://dimacs.rutgers.edu/%7Egraham/pubs/papers/cmsoft.pdf
[16] Count-Min Sketch [16]: http://dimacs.rutgers.edu/~graham/pubs/papers/cmencyc.pdf
[17] A Tree-Based Packet Routing Table for Berkeley Unix [17]: http://ece.ut.ac.ir/classpages/F83/Advanced%20Computer%20Networks/PAPERS/LOOKUP/routing.pdf
[18] Distribution-aware compressed full-text indexes [18]: https://helda.helsinki.fi/bitstream/handle/10138/27658/WeiCFI.pdf
[19] "Crit-bit" trees [19]: http://cr.yp.to/critbit.html
[20] Judy arrays [20]: http://www.nothings.org/computer/judy/
[21] The Adaptive Radix Tree: ARTful Indexing for Main-Memory Databases [21]: http://www3.in.tum.de/~leis/papers/ART.pdf
[22] Nutrient [22]: https://github.com/colmmacc/nutrient
[23] Compressing dictionaries with a DAWG. [23]: http://stevehanov.ca/blog/index.php?id=115