shuai-huang / 1Bit-CS

1-bit and multi-bit compressive sensing using approximate message passing with built-in parameter estimation

1-bit and Multi-bit Compressive Sensing via AMP with Parameter Estimation

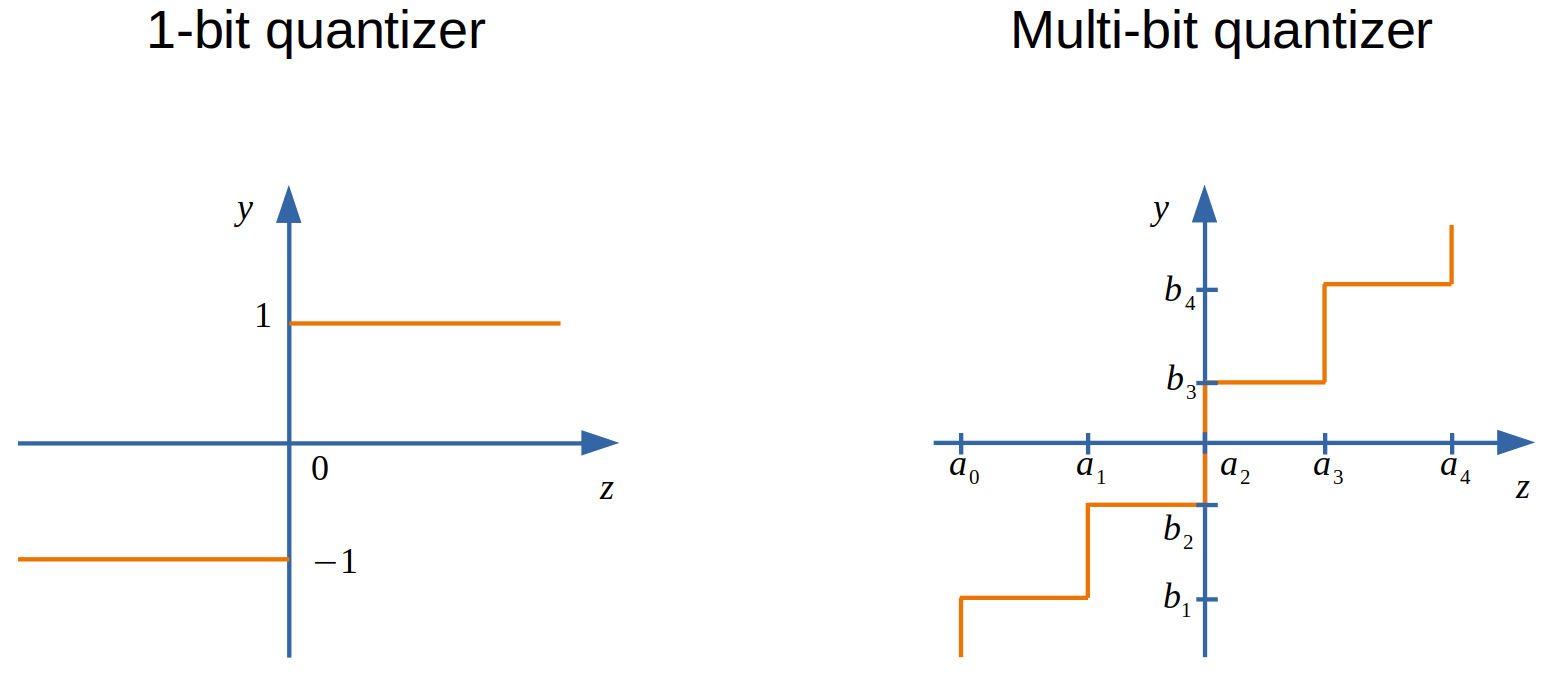
• 1-bit Compressive Sensing (CS) tries to recover a sparse signal from quantized 1-bit measurements.

• 1-bit CS can be straightforwardly extended to multi-bit CS that tries to recover a sparse signal from quantized multi-bit measurements.

• We propose to solve the two problems using the proposed AMP with built-in parameter estimation (AMP-PE) [1].

• AMP-PE offers a much simpler way to estimate the distribution parameters, which allows us to directly work with true quantization noise models. {width=100%}

• This package contains code files to implement the approach described in the following paper.

@article{QM_AMP_PE,
    author={Shuai Huang and Deqiang Qiu and Trac D. Tran},
    journal={IEEE Transactions on Signal Processing}, 
    title={Approximate Message Passing With Parameter Estimation for Heavily Quantized Measurements}, 
    year={2022},
    volume={70},
    number={},
    pages={2062-2077},
    doi={10.1109/TSP.2022.3167516}
}

If you use this package and find it helpful, please cite the above paper. Thanks 😄 {width=50%}

Summary

    ./src          -- This folder contains MATLAB files to recover the signal from 1-bit and multi-bit measurements.
    ./demo         -- This folder contains demo files to run experiments in the paper, detailed comments are within each demo file.

Usage

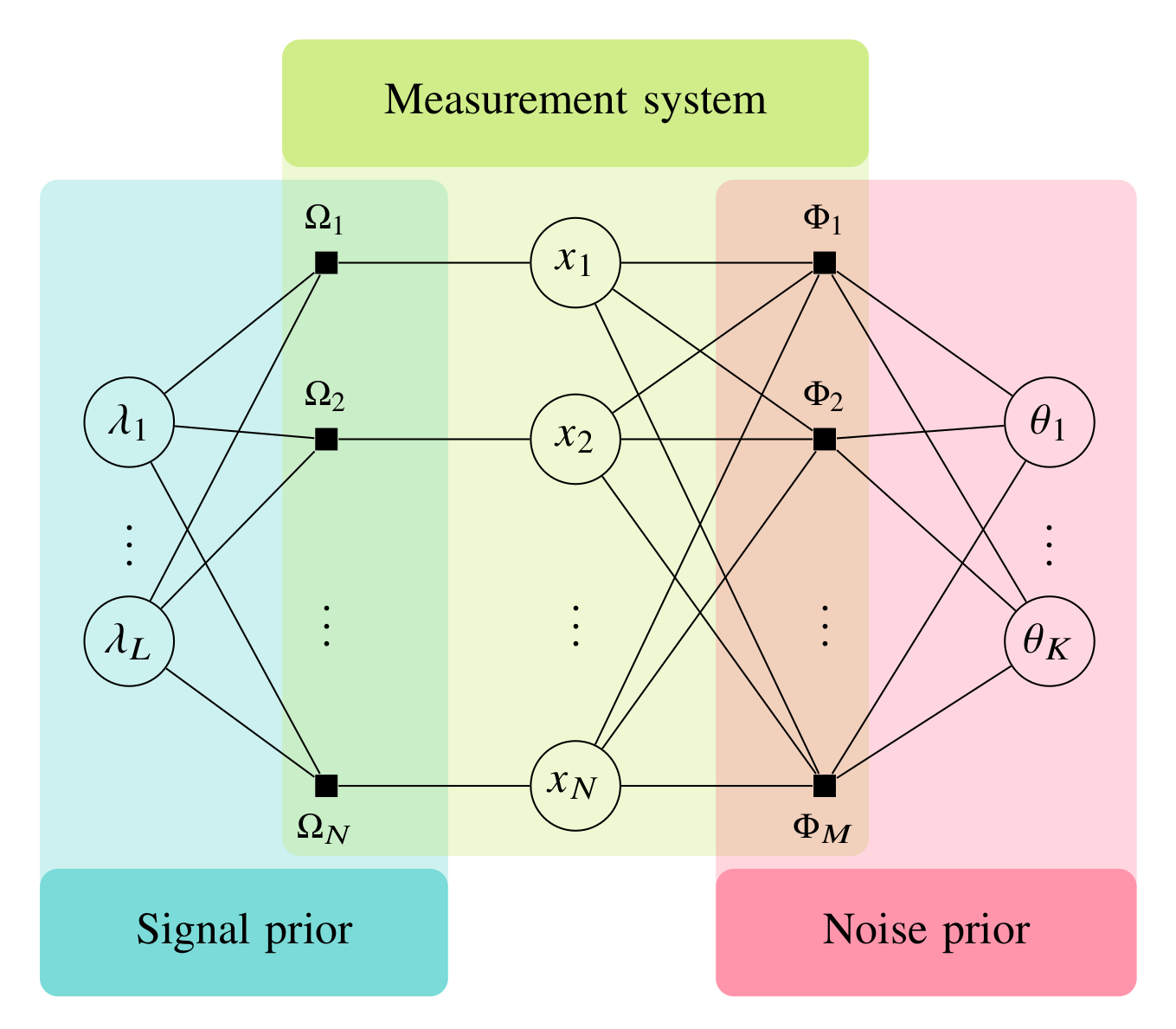
AMP-PE adopts the GAMP formulation [2] to perform message passing.

You can follow the following steps to run the program. Detailed comments are within each demo file.

Open MATLAB and type the following commands into the console:

• Step 1) Recover the signal from noisy 1-bit, 2-bit and 3-bit measurements.

    >> addpath(genpath('./'))
    >> % nonzero entries of the signal follow Gaussian distribution
    >> noisy_recovery_1bit_scalar_gaussian
    >> noisy_recovery_2bit_scalar_gaussian
    >> noisy_recovery_3bit_scalar_gaussian
    >>
    >> % nonzero entries of the signal follow Cauchy distribution
    >> noisy_recovery_1bit_scalar_cauchy
    >> noisy_recovery_2bit_scalar_cauchy
    >> noisy_recovery_3bit_scalar_cauchy
    >>
    >> % nonzero entries of the signal follow Laplace distribution
    >> noisy_recovery_1bit_scalar_laplace
    >> noisy_recovery_2bit_scalar_laplace
    >> noisy_recovery_3bit_scalar_laplace

• Step 2) Perform State Evolution (SE) analysis of the proposed AMP-PE approach.

    >> addpath(genpath('./'))
    >> noisy_SE_1bit
    >> noisy_SE_2bit
    >> noisy_SE_3bit

• Step 3) Run the channel estimation experiments.

    >> addpath(genpath('./'))
    >> noisy_channel_estimation_1bit
    >> noisy_channel_estimation_2bit
    >> noisy_channel_estimation_3bit

Reference

[1] S. Huang and T. D. Tran, "Sparse signal recovery using generalized approximate message passing with built-in parameter estimation," in Proceedings of IEEE ICASSP, March 2017, pp. 4321–4325.

[2] S. Rangan, "Generalized approximate message passing for estimation with random linear mixing," in Proceedings of IEEE ISIT, July 2011, pp. 2168–2172.