ryanjmccall / robond-kinematics

Udacity Course Kinematics Project

Project: Kinematics Pick & Place

Project Rubric

---

Kinematic Analysis

1. Run the forward_kinematics demo and evaluate the kr210.urdf.xacro file to perform kinematic analysis of Kuka KR210 robot and derive its DH parameters.

2. Using the DH parameter table you derived earlier, create individual transformation matrices about each joint. In addition, also generate a generalized homogeneous transform between base_link and gripper_link using only end-effector(gripper) pose.

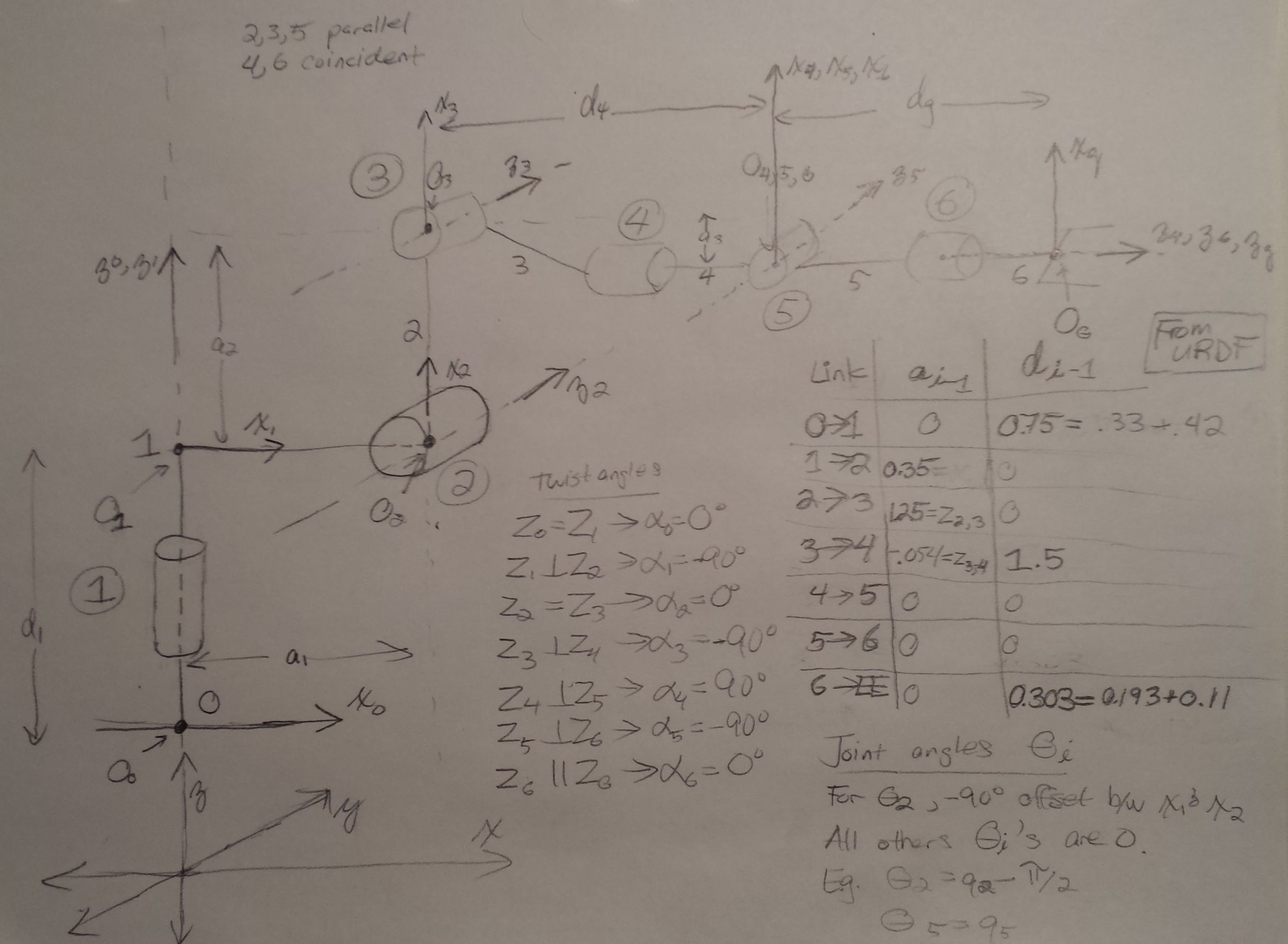
Definition of DH parameters

• Twist angle (alpha) is the angle between z_i-1 and z_i as measured about x_i-1 in the right-hand sense
• Link length (a) is the distance between z_i-1 and z_i along x_i-1 where x_i-1 is perpendicular to both z_i-1 and zi
• Link offset (d) is the signed distance from x_i-1 to x_i measure along z_i. Will be a variable for a prismatic joint.
• Joint angle (theta) is the angle between x_i-1 to x_i measured about z_i in the right-hand send. Will be a variable for a revolute joint.

From URDF file:

• J0 = (0, 0, 0)
• J1 = (0, 0, 0.33)
• J2 = (0.35, 0, 0.42)
• J3 = (0, 0, 1.25)
• J4 = (0.96, 0, -0.054)
• J5 = (0.54, 0, 0)
• J6 = (0.193, 0, 0)
• JG = (0.11, 0, 0)

Links	alpha(i-1)	a(i-1)	d(i-1)	theta(i)
0->1	0	0	0.75	q1
1->2	-pi/2	0.35	0	q2 - pi/2
2->3	0	1.25	0	q3
3->4	-pi/2	-0.054	1.5	q4
4->5	pi/2	0	0	q5
5->6	-pi/2	0	0	q6
6->EE	0	0	0.303	0

• a1 is x-axis distance beteen z1 and z2. in URDF joint 1 and joint 2 are 0.35m apart
• d1 is distance between x0 and x1 along z1, which is 0.33 + 0.42 = 0.75m

3. Decouple Inverse Kinematics problem into Inverse Position Kinematics and inverse Orientation Kinematics; doing so derive the equations to calculate all individual joint angles.

The homogeneous transform for the DH coordinates system from joint i-1 to i is:

Let T_i-1,i =

           [[cos(theta_i), -sin(theta_i), 0, a_i-1], 
           [sin(theta_i) * cos(alpha_i-1), cos(theta_i) * cos(alpha_i-1), -sin(alpha_i-1), -sin(alpha_i-1) * d_i-1], 
           [sin(theta_i) * sin(alpha_i-1), cos(theta_i) * sin(alpha_i-1), cos(alpha_i-1), cos(alpha_i-1) * d_i-1], 
           [0, 0, 0, 1]]

We fill in the alpha, a, and d values from above table and must later calculate theta values. The overall homogeneous transform from base frame to end-effector frame is them:

T_0EE = T_01 * T_12 * T_23 * T_34 * T_45 * T_56 * T_6EE

Let r=rotation, p=pitch, y=yaw, then the x, y, and z rotations in a 3D space are as follows:

rotX = [[1, 0, 0], [0, cos(r), -sin(r)], [0, sin(r), cos(r)]]
rotY = [[cos(p), 0, sin(p)], [0, 1, 0], [-sin(p), 0, cos(p)]]
rotZ = [[cos(y), -sin(y), 0], [sin(y), cos(y), 0], [0, 0, 1]]

rotationEE = rotZ * rotY * rotX

To compare results with Rviz, we must rotate the R0_G frame. That correction is given by:

rotError = rotZ(y=pi) * rotY(p=-pi/2)

correctedRotEE = rotationEE * rotError = f(r, p, y)

Inverse Kinematics

We have a spherical wrists robot with joint 5 being the wrist center. Thus we can kinematically decouple the IK problem into Inverse Position and Inverse Orientation

Inverse Position

Wrist center position determined by first three joints. Use complete transform matrix based on end-effector pose.

Define homogeneous transform as following:

[l_x m_x n_x p_x] [l_y m_y n_y p_z] [l_z m_z n_z p_z] [0 0 0 1]

where l, m, and n are orthonormal vectors representing end-effector orientation along X, Y, Z axes of local coordinate frame. Given n is vector along z-axis:

w_x = p_x - (d6 + 1) * n_x w_y = p_y - (d6 + 1) * n_y w_z = p_z - (d6 + 1) * n_zx

Where px, py, pz be the x, y, z coordinates of the end-effector

w_x, w_y, w_z = wrist positions

d6 comes from DH table

l = end-effector length

0_r_WC/0 = 0_r_EE/0 - d * 0-6R * [[0][0][1]] - [[px], [py], [pz]] - d * 0-6R [[0][0][1]]

WC = [[px], [py], [pz]] - 0.303 * correctedRotEE[:, 2]

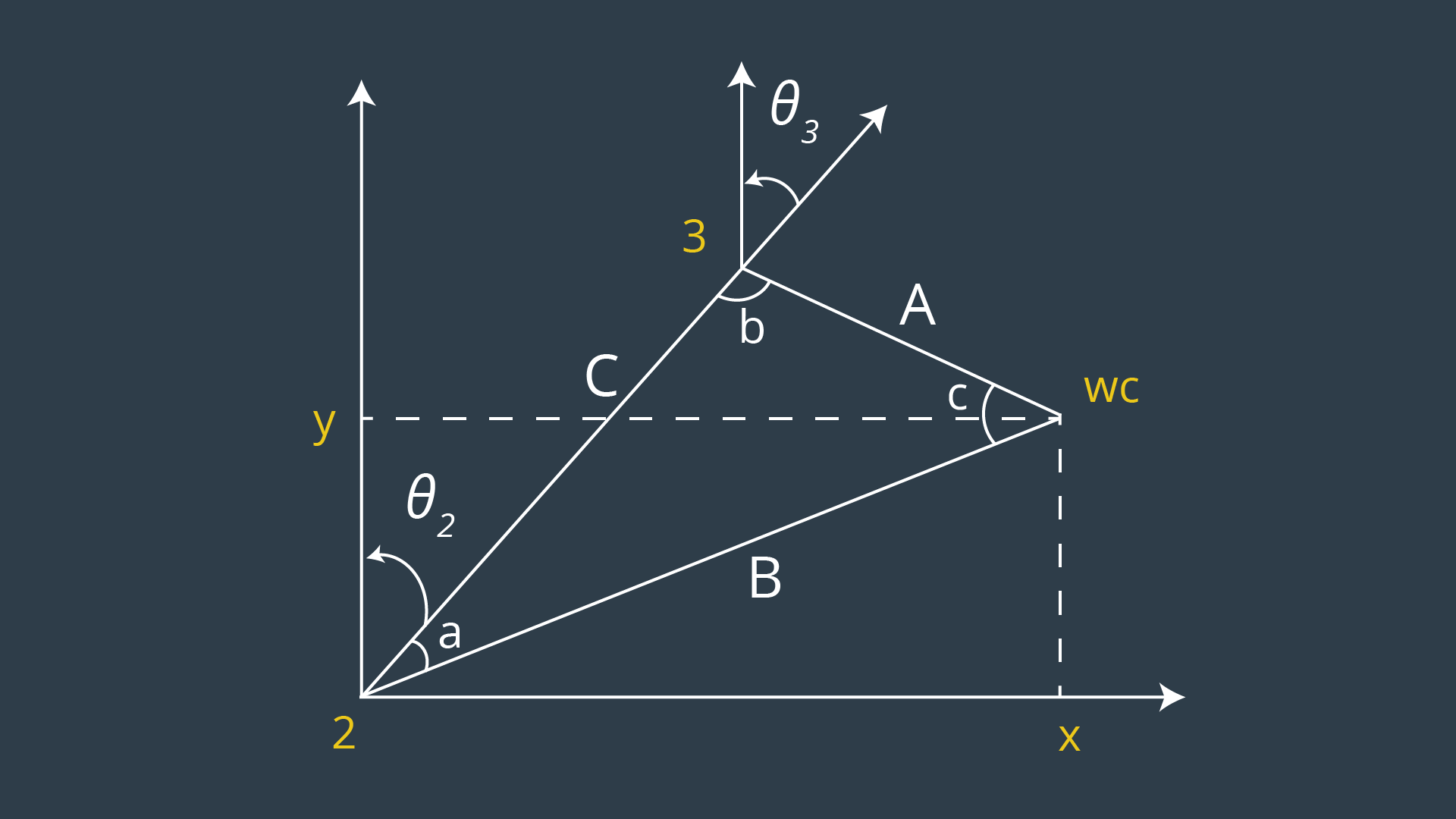
theta1 = arctan2(WC_y, WC_x)

side_a = 1.501

side_b = sqrt((sqrt(WC[0]^2 + WC[1]^2) - 0.35)^2 + (WC[2] - 0.75)^2)

side_c = 1.25

angle_a = acos((side_b^2 + side_c^2 - side_a^2) / (2 * side_b * side_c))

angle_b = acos((side_a^2 + side_c^2 - side_b^2) / (2 * side_a * side_c))

theta2 = pi/2 - angle_a - atan2(WC[2] - 0.75, sqrt(WC[0]^2 + WC[1]^2) - 0.35)

theta3 = pi/2 - (angle_b + 0.036) (constant accounts for sag in link4 of -0.054m)

Inverse Orientation

Resultant transform give by:

R0_6 = R0_1 * R1_2 * R2_3 * R3_4 * R4_5 * R5_6

Overall roll, pitch, yaw rotation from base to gripper must equal product of individual rotations between respective links, the following holds:

R0_6 = Rrpy

where Rrpy = homogeneous RPY rotation between base link gripper link

r03 = t01[0:3, 0:3] * t12[0:3, 0:3] * t23[0:3, 0:3]

r03 = r03(q1=theta1, q2=theta2, q3=theta3)

Multiplying both sides of the above equation by LU_inverse(R0_3) Calculate inverse using Sympy's inv() passing "LU" ensuring "LU decomposition." r36 = LU_inverse(r03) * correctedRotEE

Resultant matrix on the RHS does not have any variables after substituting joint angle values.

Compute Euler angles from the rotation matrix from 3-6

theta4 = atan2(r36[2, 2], -r36[0, 2])

theta5 = atan2(sqrt(r36[0, 2]^2 + r36[2, 2]^2), r36[1, 2])

theta6 = atan2(-r36[1, 1], r36[1, 0])

Project Implementation

1. Fill in the IK_server.py file with properly commented python code for calculating Inverse Kinematics based on previously performed Kinematic Analysis. Your code must guide the robot to successfully complete 8/10 pick and place cycles. Briefly discuss the code you implemented and your results.

The IK_server.py code features a class containing pre-calculated transformations to speed up the inverse kinematics calculation. In particular, this class precalculates the T_01, T_12, and T_23 DH transformation matrices as well as the corrected end-effector rotation matrix. The implementation might fail for some cases where the end-effector error is large (e.g., case 3 in the debug script). Some additional debugging and parameter tuning could help this.