reox / arls

Automatically Regularized Least Squares

ARLS: Automatically Regularized Linear System Solver

Arls is intended for use in solving linear systems, Ax=b, which other solvers may not be able to handle. Ill-conditioning is the usual reason for people to seek alternative solvers such as arls(). In addition, arls() has a rich set of constraints which can be useful in solving both difficult and easy systems.

All these solvers apply to any shape of the matrix, A. That is, the system can have more rows than columns (over-determined), or the same number of rows and columns (square), or fewer rows than columns (under-determined). And the matrix A can be full rank, or have near zero singular values, or exactly zero singular values of any number.

Please see the in-code comments for details of calls and returns, including example applications for each routine.

Our primary solver is:

from arls import arls
x = arls(A, b)

If you need to solve many systems with the same matrix, A, but different b vectors, use:

from arls import arlsusv
x = arlsusv(A, b, U, S, Vt)[0]

See details in the code comments for how to get U, S, Vt.

If you need the solution to be constrained to be non-negative, use:

from arls import arlsnn
x = arlsnn(A, b)

If you need to add constraint equations which must be satisfied exactly (such as "the sum of the solution elements must be 100.0") then put those equation in a separate system, Ex == f and call:

from arls import arlseq
x = arlseq(A, b, E, f)

If you need to add inequality constraints, such as x1 + x2 >= 1.0 then put those equations in a separate system, Gx >= h and call:

from arls import arlsgt
x = arlsgt(A, b, G, h)

If you need both equality and inequality constraints, use

from arls import arlsall
x = arlsall(A, b, E, f, G, h) 

You can also constrain the shape of the solution with

from arls import arlshape
x = arlshape(A, b, nonneg, slope, curve)

You can constrain the solution to be

1. nonnegative; and/or
2. monotonically non-decreasing (i.e., rising) or monotonically non-increasing (i.e., falling); and/or
3. concave upward (like y = x*x) or concave downward.

Examples:

x = arlshape(A, b, 1, 1, 0)  # will force x to be nonnegative and rising.
x = arlshape(A, b, 0, -1, 1)  # will force x to be falling and concave up.

See details in the code comments.

Example

This example is given in the Matlab version of ARLS: ARLS v2.

import numpy as np
import scipy
from arls import arls

# Hilbert matrix:
order = 7
A = scipy.linalg.hilbert(order)

# ideal solution:
x = np.arange(order)[::-1]

# Add noise
np.random.seed(0)
b = A @ x + np.random.normal(scale=0.0001, size=(order, ))

# Using least squares solver:
x_ls, _, _, _ = np.linalg.lstsq(A, b, rcond=None)
# Using arls:
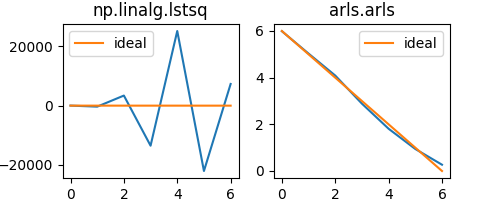
x_arls = arls(A, b)

It can clearly be noticed, that the standard least squares solver starts to oscillate and the coefficients are actually around 10000 times larger than expected. ARLS however, can find a very good solution, close to the ideal solution that is desired (of course, it cannot give the exact same solution, as we have added noise!).

Origin of the code and Matlab version

This repository was created from the source code of arls version 1.0.2 published at pypi.org.

Rondall E. Jones published a new version in 2023 for Matlab only at the Matlab File Exchange. The Matlab version was also presented in a blog entry by Cleve Moler.

There is also some more information on Rondall E. Jones' website, for example a copy of his PhD thesis.