Deep Learning models have so much flexibility and capacity that overfitting can be a serious problem, if the training dataset is not big enough. Sure it does well on the training set, but the learned network doesn't generalize to new examples that it has never seen!
In this project I am going to use regularization in this deep learning model.
Let's first import the packages that I am going to use.
# import packages
import numpy as np
import matplotlib.pyplot as plt
# pleasr refer "reg_utils.py" and "testCases.py" in the same directory for the below "reg_utils" and "testCases"libraries
from reg_utils import sigmoid, relu, plot_decision_boundary, initialize_parameters, predict_dec
from reg_utils import compute_cost, predict, forward_propagation, backward_propagation, update_parameters
import sklearn
import sklearn.datasets
import scipy.io
from testCases import *
%matplotlib inline
plt.rcParams['figure.figsize'] = (7.0, 4.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
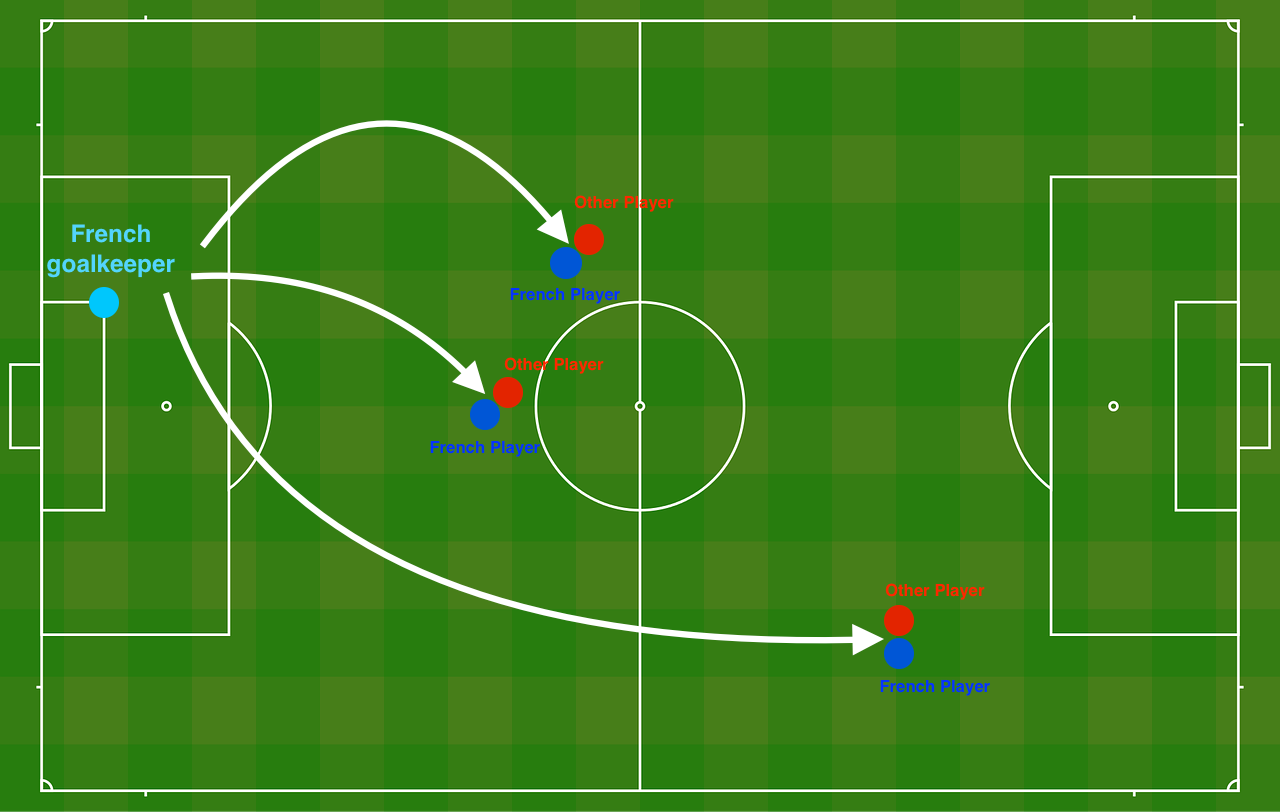
plt.rcParams['image.cmap'] = 'gray'For this project, I am going to recommend positions where France's goal keeper should kick the ball so that the French team's players can then hit it with their head. Later, I can give this recommendations to French Football Corporation as an AI expert :)
**Figure 1** : **Football field**The goal keeper kicks the ball in the air, the players of each team are fighting to hit the ball with their head
def load_2D_dataset():
data = scipy.io.loadmat('data.mat')
train_X = data['X'].T
train_Y = data['y'].T
test_X = data['Xval'].T
test_Y = data['yval'].T
plt.scatter(train_X[0, :], train_X[1, :], c=train_Y[0], s=40, cmap=plt.cm.Spectral);
return train_X, train_Y, test_X, test_Y
train_X, train_Y, test_X, test_Y = load_2D_dataset()
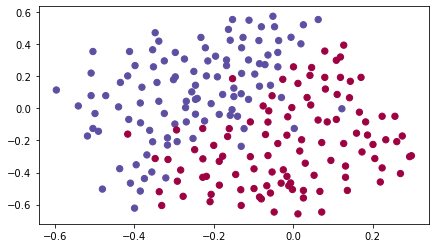
# Following 2D dataset from France's past 10 games.Each dot corresponds to a position on the football field where a football player has hit the ball with his/her head after the French goal keeper has shot the ball from the left side of the football field.
- If the dot is blue, it means the French player managed to hit the ball with his/her head
- If the dot is red, it means the other team's player hit the ball with their head
My goal is to use a deep learning model to find the positions on the field where the goalkeeper should kick the ball.
Analysis of the dataset: This dataset is a little noisy, but it looks like a diagonal line separating the upper left half (blue) from the lower right half (red) would work well.
I will first try a non-regularized model. Then I'll try to regularize it and decide which model that I will choose to solve the French Football Corporation's problem.
I am using the following neural network. This model can be used:
- in regularization mode -- by setting the
lambdinput to a non-zero value. We use "lambd" instead of "lambda" because "lambda" is a reserved keyword in Python. - in dropout mode -- by setting the
keep_probto a value less than one
I will first try the model without any regularization. Then, I will implement:
- L2 regularization -- functions: "
compute_cost_with_regularization()" and "backward_propagation_with_regularization()" - Dropout -- functions: "
forward_propagation_with_dropout()" and "backward_propagation_with_dropout()"
Before you proceed please refer "reg_utils.py" and "testCases.py" in the same directory. It will provide all the dropout functions that I am goinng to use tin this project.
In each part, I will run this model with the correct inputs so that it calls the functions that I've implemented. Take a look at the code below to familiarize yourself with the model.
def model(X, Y, learning_rate = 0.3, num_iterations = 30000, print_cost = True, lambd = 0, keep_prob = 1):
"""
Implements a three-layer neural network: LINEAR->RELU->LINEAR->RELU->LINEAR->SIGMOID.
Arguments:
X -- input data, of shape (input size, number of examples)
Y -- true "label" vector (1 for blue dot / 0 for red dot), of shape (output size, number of examples)
learning_rate -- learning rate of the optimization
num_iterations -- number of iterations of the optimization loop
print_cost -- If True, print the cost every 10000 iterations
lambd -- regularization hyperparameter, scalar
keep_prob - probability of keeping a neuron active during drop-out, scalar.
Returns:
parameters -- parameters learned by the model. They can then be used to predict.
"""
grads = {}
costs = [] # to keep track of the cost
m = X.shape[1] # number of examples
layers_dims = [X.shape[0], 20, 3, 1]
# Initialize parameters dictionary.
parameters = initialize_parameters(layers_dims)
# Loop (gradient descent)
for i in range(0, num_iterations):
# Forward propagation: LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID.
if keep_prob == 1:
a3, cache = forward_propagation(X, parameters)
elif keep_prob < 1:
a3, cache = forward_propagation_with_dropout(X, parameters, keep_prob)
# Cost function
if lambd == 0:
cost = compute_cost(a3, Y)
else:
cost = compute_cost_with_regularization(a3, Y, parameters, lambd)
# Backward propagation.
assert(lambd==0 or keep_prob==1) # it is possible to use both L2 regularization and dropout,
# but this assignment will only explore one at a time
if lambd == 0 and keep_prob == 1:
grads = backward_propagation(X, Y, cache)
elif lambd != 0:
grads = backward_propagation_with_regularization(X, Y, cache, lambd)
elif keep_prob < 1:
grads = backward_propagation_with_dropout(X, Y, cache, keep_prob)
# Update parameters.
parameters = update_parameters(parameters, grads, learning_rate)
# Print the loss every 10000 iterations
if print_cost and i % 10000 == 0:
print("Cost after iteration {}: {}".format(i, cost))
if print_cost and i % 1000 == 0:
costs.append(cost)
# plot the cost
plt.plot(costs)
plt.ylabel('cost')
plt.xlabel('iterations (x1,000)')
plt.title("Learning rate =" + str(learning_rate))
plt.show()
return parametersLet's train the model without any regularization, and observe the accuracy on the train/test sets.
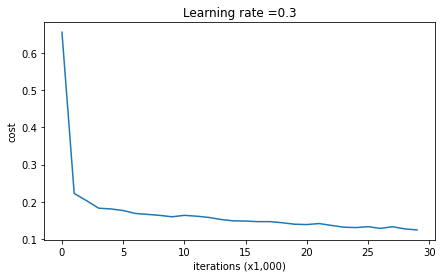
parameters = model(train_X, train_Y)
print ("On the training set:")
predictions_train = predict(train_X, train_Y, parameters)
print ("On the test set:")
predictions_test = predict(test_X, test_Y, parameters)Cost after iteration 0: 0.6557412523481002
Cost after iteration 10000: 0.16329987525724213
Cost after iteration 20000: 0.1385164242326018
On the training set:
Accuracy: 0.9478672985781991
On the test set:
Accuracy: 0.915
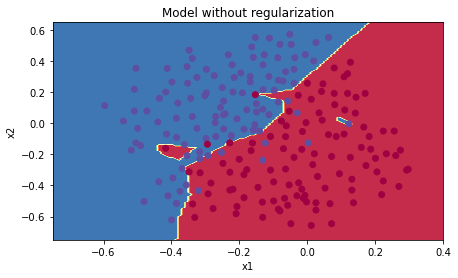
The train accuracy is 94.7% while the test accuracy is 91.5%. This is the baseline model (I am going to observe the impact of regularization on this model). Run the following code to plot the decision boundary of the model.
plt.title("Model without regularization")
axes = plt.gca()
axes.set_xlim([-0.75,0.40])
axes.set_ylim([-0.75,0.65])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)The non-regularized model is obviously overfitting the training set. It is fitting the noisy points! Lets now look at two techniques to reduce overfitting.
The standard way to avoid overfitting is called L2 regularization. It consists of appropriately modifying the cost function, from: $$J = -\frac{1}{m} \sum\limits_{i = 1}^{m} \large{(}\small y^{(i)}\log\left(a^{L}\right) + (1-y^{(i)})\log\left(1- a^{L}\right) \large{)} \tag{1}$$ To: $$J_{regularized} = \small \underbrace{-\frac{1}{m} \sum\limits_{i = 1}^{m} \large{(}\small y^{(i)}\log\left(a^{L}\right) + (1-y^{(i)})\log\left(1- a^{L}\right) \large{)} }\text{cross-entropy cost} + \underbrace{\frac{1}{m} \frac{\lambda}{2} \sum\limits_l\sum\limits_k\sum\limits_j W{k,j}^{[l]2} }_\text{L2 regularization cost} \tag{2}$$
Let's modify the cost and observe the consequences.
Exercise: Implement compute_cost_with_regularization() which computes the cost given by formula (2). To calculate
np.sum(np.square(Wl))Note that you have to do this for
# GRADED FUNCTION: compute_cost_with_regularization
def compute_cost_with_regularization(A3, Y, parameters, lambd):
"""
Implement the cost function with L2 regularization. See formula (2) above.
Arguments:
A3 -- post-activation, output of forward propagation, of shape (output size, number of examples)
Y -- "true" labels vector, of shape (output size, number of examples)
parameters -- python dictionary containing parameters of the model
Returns:
cost - value of the regularized loss function (formula (2))
"""
m = Y.shape[1]
W1 = parameters["W1"]
W2 = parameters["W2"]
W3 = parameters["W3"]
cross_entropy_cost = compute_cost(A3, Y) # This gives the cross-entropy part of the cost
L2_regularization_cost = (1./m*lambd/2)*(np.sum(np.square(W1)) + np.sum(np.square(W2)) + np.sum(np.square(W3)))
cost = cross_entropy_cost + L2_regularization_cost
return costA3, Y_assess, parameters = compute_cost_with_regularization_test_case()
print("cost = " + str(compute_cost_with_regularization(A3, Y_assess, parameters, lambd = 0.1)))cost = 1.7864859451590758
Of course, because I have changed the cost, Now I have to change backward propagation as well! All the gradients have to be computed with respect to this new cost.
Cool!!!! Now, below code will implement the changes needed in backward propagation to take into account regularization. The changes only concern dW1, dW2 and dW3. For each, I have to add the regularization term's gradient (
# GRADED FUNCTION: backward_propagation_with_regularization
def backward_propagation_with_regularization(X, Y, cache, lambd):
"""
Implements the backward propagation of our baseline model to which we added an L2 regularization.
Arguments:
X -- input dataset, of shape (input size, number of examples)
Y -- "true" labels vector, of shape (output size, number of examples)
cache -- cache output from forward_propagation()
lambd -- regularization hyperparameter, scalar
Returns:
gradients -- A dictionary with the gradients with respect to each parameter, activation and pre-activation variables
"""
m = X.shape[1]
(Z1, A1, W1, b1, Z2, A2, W2, b2, Z3, A3, W3, b3) = cache
dZ3 = A3 - Y
dW3 = 1./m * np.dot(dZ3, A2.T) + lambd/m * W3
db3 = 1./m * np.sum(dZ3, axis=1, keepdims = True)
dA2 = np.dot(W3.T, dZ3)
dZ2 = np.multiply(dA2, np.int64(A2 > 0))
dW2 = 1./m * np.dot(dZ2, A1.T) + lambd/m * W2
db2 = 1./m * np.sum(dZ2, axis=1, keepdims = True)
dA1 = np.dot(W2.T, dZ2)
dZ1 = np.multiply(dA1, np.int64(A1 > 0))
dW1 = 1./m * np.dot(dZ1, X.T) + lambd/m * W1
db1 = 1./m * np.sum(dZ1, axis=1, keepdims = True)
gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3,"dA2": dA2,
"dZ2": dZ2, "dW2": dW2, "db2": db2, "dA1": dA1,
"dZ1": dZ1, "dW1": dW1, "db1": db1}
return gradientsX_assess, Y_assess, cache = backward_propagation_with_regularization_test_case()
grads = backward_propagation_with_regularization(X_assess, Y_assess, cache, lambd = 0.7)
print ("dW1 = "+ str(grads["dW1"]))
print ("dW2 = "+ str(grads["dW2"]))
print ("dW3 = "+ str(grads["dW3"]))dW1 = [[-0.25604646 0.12298827 -0.28297129]
[-0.17706303 0.34536094 -0.4410571 ]]
dW2 = [[ 0.79276486 0.85133918]
[-0.0957219 -0.01720463]
[-0.13100772 -0.03750433]]
dW3 = [[-1.77691347 -0.11832879 -0.09397446]]
Let's now run the model with L2 regularization model() function will call:
compute_cost_with_regularizationinstead ofcompute_costbackward_propagation_with_regularizationinstead ofbackward_propagation
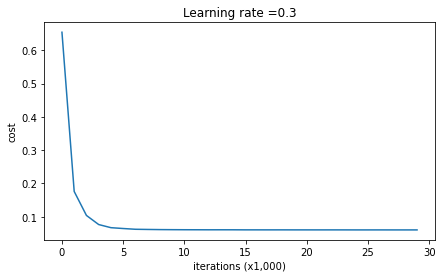
parameters = model(train_X, train_Y, lambd = 0.7)
print ("On the train set:")
predictions_train = predict(train_X, train_Y, parameters)
print ("On the test set:")
predictions_test = predict(test_X, test_Y, parameters)Cost after iteration 0: 0.6974484493131264
Cost after iteration 10000: 0.2684918873282238
Cost after iteration 20000: 0.26809163371273004
On the train set:
Accuracy: 0.9383886255924171
On the test set:
Accuracy: 0.93
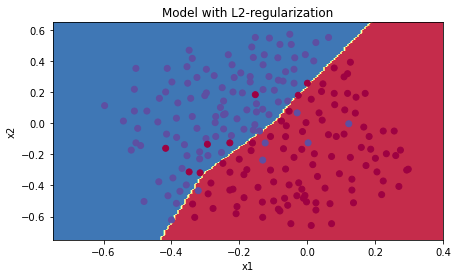
WOW 😮, the test set accuracy increased to 93%. I have saved the French football team!
Now, I am not overfitting the training data anymore. Let's plot the decision boundary.
plt.title("Model with L2-regularization")
axes = plt.gca()
axes.set_xlim([-0.75,0.40])
axes.set_ylim([-0.75,0.65])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)Observations:
- The value of
$\lambda$ is a hyperparameter that I can tune using a dev set. - L2 regularization makes my decision boundary smoother. If
$\lambda$ is too large, it is also possible to "oversmooth", resulting in a model with high bias.
What is L2-regularization actually doing?:
L2-regularization relies on the assumption that a model with small weights is simpler than a model with large weights. Thus, by penalizing the square values of the weights in the cost function you drive all the weights to smaller values. It becomes too costly for the cost to have large weights! This leads to a smoother model in which the output changes more slowly as the input changes.
What I should remember
-
The implications of L2-regularization on:
-
The cost computation:
- A regularization term is added to the cost
-
The backpropagation function:
- There are extra terms in the gradients with respect to weight matrices
-
Weights end up smaller ("weight decay"):
- Weights are pushed to smaller values.
-
Finally, dropout is a widely used regularization technique that is specific to deep learning. It randomly shuts down some neurons in each iteration. Watch these two videos to see what this means!
Figure 2 : Drop-out on the second hidden layer.
At each iteration, I shut down (= set to zero) each neuron of a layer with probability $1 - keep\_prob$ or keep it with probability $keep\_prob$ (50% here). The dropped neurons don't contribute to the training in both the forward and backward propagations of the iteration. Figure 3 : Drop-out on the first and third hidden layers.
$1^{st}$ layer: I have shut down on average 40% of the neurons. $3^{rd}$ layer: I have shut down on average 20% of the neurons.
When I shut some neurons down, I am actually modifying the model. The idea behind drop-out is that at each iteration, I have train a different model that uses only a subset of my neurons. With dropout, my neurons thus become less sensitive to the activation of one other specific neuron, because that other neuron might be shut down at any time.
Now, I am Implementing the forward propagation with dropout. I am using a 3 layer neural network, and will add dropout to the first and second hidden layers. I will not apply dropout to the input layer or output layer.
# GRADED FUNCTION: forward_propagation_with_dropout
def forward_propagation_with_dropout(X, parameters, keep_prob = 0.5):
"""
Implements the forward propagation: LINEAR -> RELU + DROPOUT -> LINEAR -> RELU + DROPOUT -> LINEAR -> SIGMOID.
Arguments:
X -- input dataset, of shape (2, number of examples)
parameters -- python dictionary containing your parameters "W1", "b1", "W2", "b2", "W3", "b3":
W1 -- weight matrix of shape (20, 2)
b1 -- bias vector of shape (20, 1)
W2 -- weight matrix of shape (3, 20)
b2 -- bias vector of shape (3, 1)
W3 -- weight matrix of shape (1, 3)
b3 -- bias vector of shape (1, 1)
keep_prob - probability of keeping a neuron active during drop-out, scalar
Returns:
A3 -- last activation value, output of the forward propagation, of shape (1,1)
cache -- tuple, information stored for computing the backward propagation
"""
np.random.seed(1)
# retrieve parameters
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
W3 = parameters["W3"]
b3 = parameters["b3"]
# LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID
Z1 = np.dot(W1, X) + b1
A1 = relu(Z1)
# Steps 1-4 below correspond to the Steps 1-4 described above.
D1 = np.random.rand(A1.shape[0],A1.shape[1]) # Step 1: initialize matrix D1 = np.random.rand(..., ...)
D1 = D1 < keep_prob # Step 2: convert entries of D1 to 0 or 1 (using keep_prob as the threshold)
A1 = A1 * D1 # Step 3: shut down some neurons of A1
A1 = A1 / keep_prob # Step 4: scale the value of neurons that haven't been shut down
Z2 = np.dot(W2, A1) + b2
A2 = relu(Z2)
D2 = np.random.rand(A2.shape[0],A2.shape[1]) # Step 1: initialize matrix D2 = np.random.rand(..., ...)
D2 = D2 < keep_prob # Step 2: convert entries of D2 to 0 or 1 (using keep_prob as the threshold)
A2 = A2 * D2 # Step 3: shut down some neurons of A2
A2 = A2 / keep_prob # Step 4: scale the value of neurons that haven't been shut down
Z3 = np.dot(W3, A2) + b3
A3 = sigmoid(Z3)
cache = (Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3)
return A3, cacheX_assess, parameters = forward_propagation_with_dropout_test_case()
A3, cache = forward_propagation_with_dropout(X_assess, parameters, keep_prob = 0.7)
print ("A3 = " + str(A3))A3 = [[0.36974721 0.00305176 0.04565099 0.49683389 0.36974721]]
Implementing the backward propagation with dropout. As before, I am training a 3 layer network and adding dropout to the first and second hidden layers, using the masks D^{[1]} and D^{[2]} stored in the cache.
Instruction: Backpropagation with dropout is actually quite easy. You will have to carry out 2 Steps:
- I have previously shut down some neurons during forward propagation, by applying a mask D^{[1]} to
A1. In backpropagation, I will have to shut down the same neurons, by reapplying the same mask D^{[1]} todA1. - During forward propagation, I have divided
A1bykeep_prob. In backpropagation, I'll therefore have to dividedA1bykeep_probagain (the calculus interpretation is that if A^{[1]} is scaled bykeep_prob, then its derivative dA^{[1]} is also scaled by the samekeep_prob).
# GRADED FUNCTION: backward_propagation_with_dropout
def backward_propagation_with_dropout(X, Y, cache, keep_prob):
"""
Implements the backward propagation of our baseline model to which we added dropout.
Arguments:
X -- input dataset, of shape (2, number of examples)
Y -- "true" labels vector, of shape (output size, number of examples)
cache -- cache output from forward_propagation_with_dropout()
keep_prob - probability of keeping a neuron active during drop-out, scalar
Returns:
gradients -- A dictionary with the gradients with respect to each parameter, activation and pre-activation variables
"""
m = X.shape[1]
(Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3) = cache
dZ3 = A3 - Y
dW3 = 1./m * np.dot(dZ3, A2.T)
db3 = 1./m * np.sum(dZ3, axis=1, keepdims = True)
dA2 = np.dot(W3.T, dZ3)
dA2 = dA2 * D2 # Step 1: Apply mask D2 to shut down the same neurons as during the forward propagation
dA2 = dA2 / keep_prob # Step 2: Scale the value of neurons that haven't been shut down
dZ2 = np.multiply(dA2, np.int64(A2 > 0))
dW2 = 1./m * np.dot(dZ2, A1.T)
db2 = 1./m * np.sum(dZ2, axis=1, keepdims = True)
dA1 = np.dot(W2.T, dZ2)
dA1 = dA1 * D1 # Step 1: Apply mask D1 to shut down the same neurons as during the forward propagation
dA1 = dA1 / keep_prob # Step 2: Scale the value of neurons that haven't been shut down
dZ1 = np.multiply(dA1, np.int64(A1 > 0))
dW1 = 1./m * np.dot(dZ1, X.T)
db1 = 1./m * np.sum(dZ1, axis=1, keepdims = True)
gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3,"dA2": dA2,
"dZ2": dZ2, "dW2": dW2, "db2": db2, "dA1": dA1,
"dZ1": dZ1, "dW1": dW1, "db1": db1}
return gradientsX_assess, Y_assess, cache = backward_propagation_with_dropout_test_case()
gradients = backward_propagation_with_dropout(X_assess, Y_assess, cache, keep_prob = 0.8)
print ("dA1 = " + str(gradients["dA1"]))
print ("dA2 = " + str(gradients["dA2"]))dA1 = [[ 0.36544439 0. -0.00188233 0. -0.17408748]
[ 0.65515713 0. -0.00337459 0. -0. ]]
dA2 = [[ 0.58180856 0. -0.00299679 0. -0.27715731]
[ 0. 0.53159854 -0. 0.53159854 -0.34089673]
[ 0. 0. -0.00292733 0. -0. ]]
Let's now run the model with dropout (keep_prob = 0.86). It means at every iteration I ahvve shut down each neurons of layer 1 and 2 with 24% probability. The function model() will now call:
forward_propagation_with_dropoutinstead offorward_propagation.backward_propagation_with_dropoutinstead ofbackward_propagation.
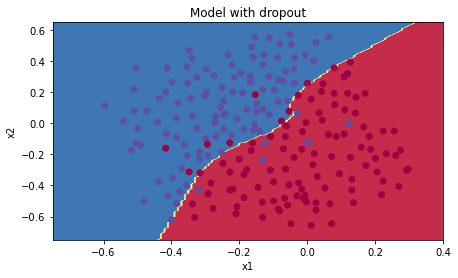
parameters = model(train_X, train_Y, keep_prob = 0.86, learning_rate = 0.3)
print ("On the train set:")
predictions_train = predict(train_X, train_Y, parameters)
print ("On the test set:")
predictions_test = predict(test_X, test_Y, parameters)Cost after iteration 0: 0.6543912405149825
/Users/rajeshidumalla/reg_utils.py:236: RuntimeWarning: divide by zero encountered in log
logprobs = np.multiply(-np.log(a3),Y) + np.multiply(-np.log(1 - a3), 1 - Y)
/Users/rajeshidumalla/reg_utils.py:236: RuntimeWarning: invalid value encountered in multiply
logprobs = np.multiply(-np.log(a3),Y) + np.multiply(-np.log(1 - a3), 1 - Y)
Cost after iteration 10000: 0.061016986574905605
Cost after iteration 20000: 0.060582435798513114
On the train set:
Accuracy: 0.9289099526066351
On the test set:
Accuracy: 0.95
Dropout works great! The test accuracy has increased again (to 95%)! My model is not overfitting the training set and does a great job on the test set. The French football team will be forever grateful to me!
Run the code below to plot the decision boundary.
plt.title("Model with dropout")
axes = plt.gca()
axes.set_xlim([-0.75,0.40])
axes.set_ylim([-0.75,0.65])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)Note:
- A common mistake when using dropout is to use it both in training and testing. You should use dropout (randomly eliminate nodes) only in training.
- Deep learning frameworks like tensorflow, PaddlePaddle, keras or caffe come with a dropout layer implementation.
- Dropout is a regularization technique.
- I do only use dropout during training and not using dropout (randomly eliminate nodes) during test time.
- Applying dropout both during forward and backward propagation.
- During training time, divide each dropout layer by keep_prob to keep the same expected value for the activations. For example, if keep_prob is 0.5, then we will on average shut down half the nodes, so the output will be scaled by 0.5 since only the remaining half are contributing to the solution. Dividing by 0.5 is equivalent to multiplying by 2. Hence, the output now has the same expected value. we can check that this works even when keep_prob is other values than 0.5.
3-layer NN without regularization:
- On the training set accuracy: 94.7%
- On the test set accracy: 91.5%
3-layer NN with L2-regularization:
- On the train set accuracy: 93.8%
- On the test set accuracy: 93%
3-layer NN with dropout:
- On the train set accuracy: 92.8%
- On the test set accuracy: 95%
I have learned that regularization hurts training set performance! This is because it limits the ability of the network to overfit to the training set. But since it ultimately gives better test accuracy, it is helping my system.
- Regularization will help to reduce overfitting.
- Regularization will drive weights to lower values.
- L2 regularization and Dropout are two very effective regularization techniques.