qutang / mixture-of-experts

A Pytorch implementation of Sparsely-Gated Mixture of Experts, for massively increasing the parameter count of language models

Sparsely Gated Mixture of Experts - Pytorch

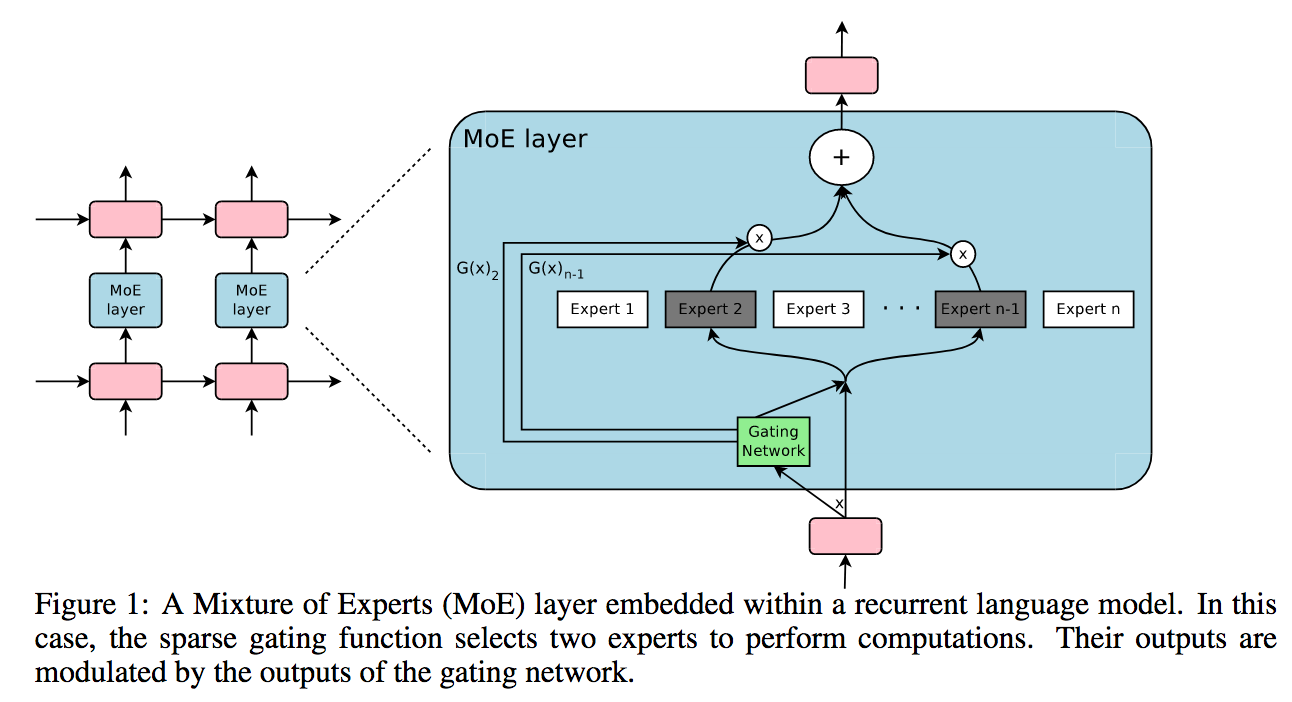
A Pytorch implementation of Sparsely Gated Mixture of Experts, for massively increasing the capacity (parameter count) of a language model while keeping the computation constant.

It will mostly be a line-by-line transcription of the tensorflow implementation here, with a few enhancements.

Install

$ pip install mixture_of_experts

Usage

import torch
from torch import nn
from mixture_of_experts import MoE

moe = MoE(
    dim = 512,
    num_experts = 16,               # increase the experts (# parameters) of your model without increasing computation
    hidden_dim = 512 * 4,           # size of hidden dimension in each expert, defaults to 4 * dimension
    activation = nn.LeakyReLU,      # use your preferred activation, will default to GELU
    second_policy_train = 'random', # in top_2 gating, policy for whether to use a second-place expert
    second_policy_eval = 'random',  # all (always) | none (never) | threshold (if gate value > the given threshold) | random (if gate value > threshold * random_uniform(0, 1))
    second_threshold_train = 0.2,
    second_threshold_eval = 0.2,
    capacity_factor_train = 1.25,   # experts have fixed capacity per batch. we need some extra capacity in case gating is not perfectly balanced.
    capacity_factor_eval = 2.,      # capacity_factor_* should be set to a value >=1
    loss_coef = 1e-2                # multiplier on the auxiliary expert balancing auxiliary loss
)

inputs = torch.randn(4, 1024, 512)
out, aux_loss = moe(inputs) # (4, 1024, 512), (1,)

The above should suffice for a single machine, but if you want a heirarchical mixture of experts (2 levels), as used in the GShard paper, please follow the instructions below

import torch
from mixture_of_experts import HeirarchicalMoE

moe = HeirarchicalMoE(
    dim = 512,
    num_experts = (4, 4),       # 4 gates on the first layer, then 4 experts on the second, equaling 16 experts
)

inputs = torch.randn(4, 1024, 512)
out, aux_loss = moe(inputs) # (4, 1024, 512), (1,)

1 billion parameters

import torch
from mixture_of_experts import HeirarchicalMoE

moe = HeirarchicalMoE(
    dim = 512,
    num_experts = (22, 22)
).cuda()

inputs = torch.randn(1, 1024, 512).cuda()
out, aux_loss = moe(inputs)

total_params = sum(p.numel() for p in moe.parameters())
print(f'number of parameters - {total_params}')

If you want some more sophisticated network for the experts, you can define your own and pass it into the MoE class as experts

import torch
from torch import nn
from mixture_of_experts import MoE

# a 3 layered MLP as the experts

class Experts(nn.Module):
    def __init__(self, dim, num_experts = 16):
        super().__init__()
        self.w1 = nn.Parameter(torch.randn(num_experts, dim, dim * 4))
        self.w2 = nn.Parameter(torch.randn(num_experts, dim * 4, dim * 4))
        self.w3 = nn.Parameter(torch.randn(num_experts, dim * 4, dim))
        self.act = nn.LeakyReLU(inplace = True)

    def forward(self, x):
        hidden1 = self.act(torch.einsum('end,edh->enh', x, self.w1))
        hidden2 = self.act(torch.einsum('end,edh->enh', hidden1, self.w2))
        out = torch.einsum('end,edh->enh', hidden2, self.w3)
        return out

experts = Experts(512, num_experts = 16)

moe = MoE(
    dim = 512,
    num_experts = 16,
    experts = experts
)

inputs = torch.randn(4, 1024, 512)
out, aux_loss = moe(inputs) # (4, 1024, 512), (1,)

Citation

@misc{shazeer2017outrageously,
    title   = {Outrageously Large Neural Networks: The Sparsely-Gated Mixture-of-Experts Layer},
    author  = {Noam Shazeer and Azalia Mirhoseini and Krzysztof Maziarz and Andy Davis and Quoc Le and Geoffrey Hinton and Jeff Dean},
    year    = {2017},
    eprint  = {1701.06538},
    archivePrefix = {arXiv},
    primaryClass = {cs.LG}
}

@misc{lepikhin2020gshard,
    title   = {GShard: Scaling Giant Models with Conditional Computation and Automatic Sharding},
    author  = {Dmitry Lepikhin and HyoukJoong Lee and Yuanzhong Xu and Dehao Chen and Orhan Firat and Yanping Huang and Maxim Krikun and Noam Shazeer and Zhifeng Chen},
    year    = {2020},
    eprint  = {2006.16668},
    archivePrefix = {arXiv},
    primaryClass = {cs.CL}
}