Provides MatLab implementations of the classic integrate-and-fire model of a neuron using both numerical simulation and theoretical derivation.
integrate_and_fire.m contains a functional implementation of the Integrate-and-Fire neuron
in the integrate_and_fire function. This function takes in a vector I_e that contains one
entry per time point for the applied current to the neuron at that time point. It also takes in
delta_t, or the time increment being used for the calculations, and t_total, the total amount
of time for which we will simulate the neuron. This function models the neuron using the standard
integrate-and-fire differential equation with the input delta_t and returns arrays corresponding to
x (time) and y (membrane potential) which may be used in plotting, as well as a count of the number
of spikes the neuron reached during the simulation.
plot_helper.m provides a simple helper function that may be called with x and y vectors and a title
string ttl and plots the results of the Integrate-and-Fire model, including appropriate axis labels.
theoretical_firing.m takes in an applied current I_e (here I_e is a single number rather
than a vector), and calculates T, the time between two spikes, based on theoretical derivations
from the traditional Integrate-and-Fire differential equation.
V_t.m takes in the resting membrane potential E_L and the membrane time constant Tau_m
and calculates the progression of the Integrate-and-Fire model over 100 time points based on the
solved differential equation. These results could be compared to the numeric simulation as implemented
in integrate_and_fire.m
main.m conducts all of our main computations, separated by problem as follows:
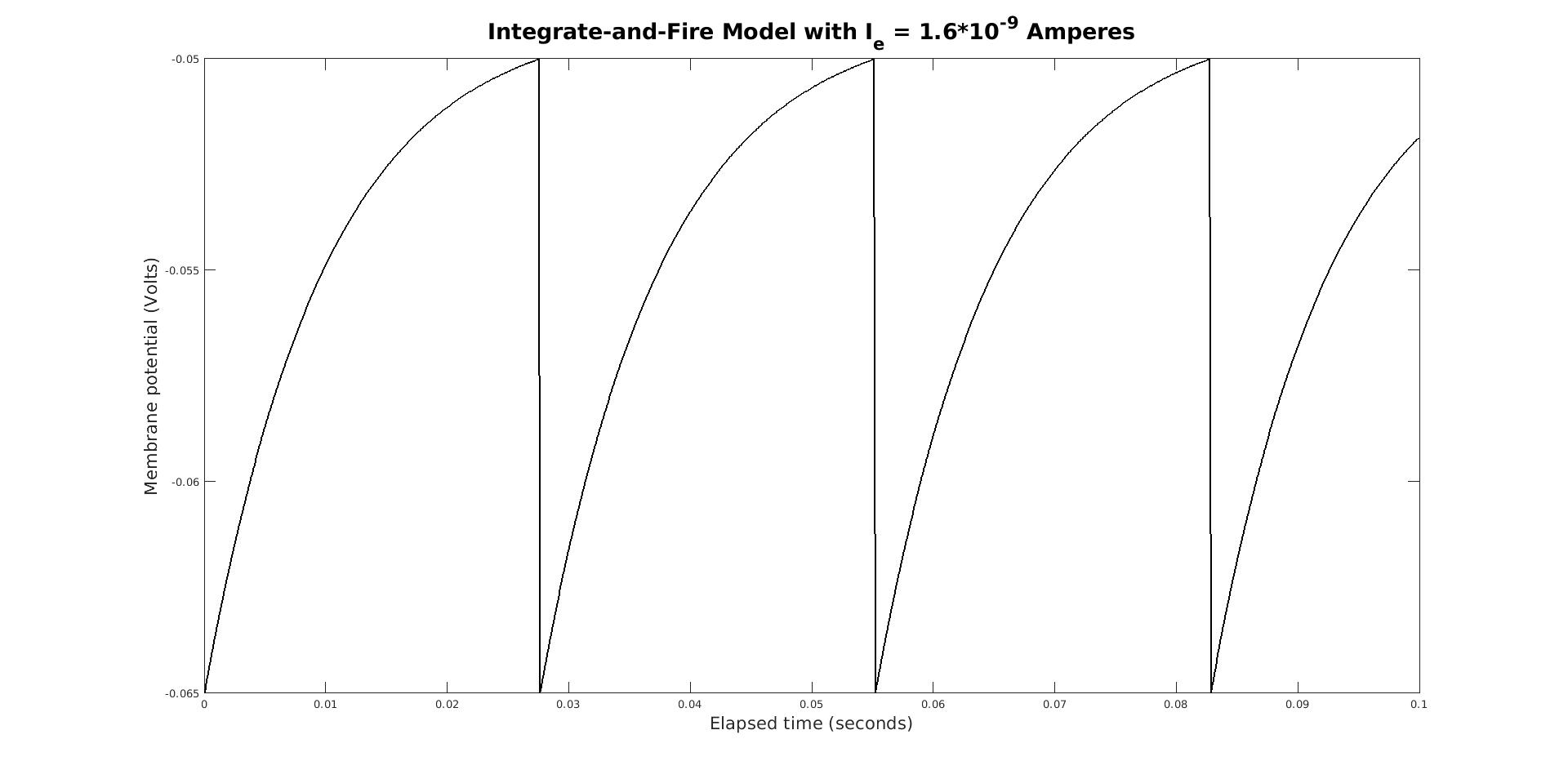
We begin by testing the most basic implementation fo the Integrate-and-Fire model by keeping I_e constant
across time and calling integrate_and_fire to compare different values of I_e and graphing the results by
calling the plot_helper function. For example, for I_e = 1.6*10^-9 amperes, our integrate_and_fire model
yields the following:
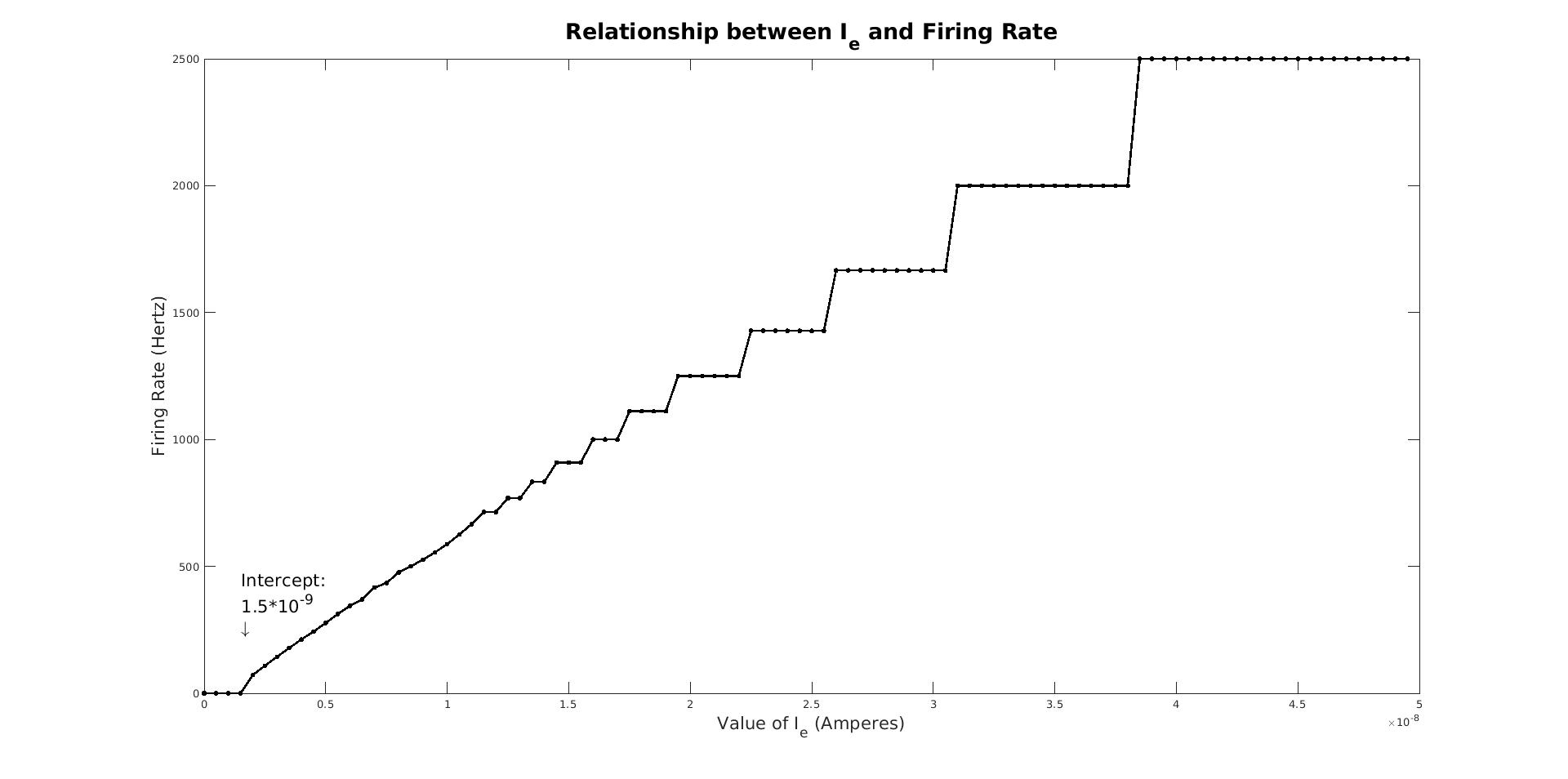
While investigating the effects of a constant I_e, we also consider the relationship between the magnitude of
the external current and the firing rate, measured as the number of spikes per second, by running integrate_and_fire
for one second on a variety of constant I_es. The following step-wise relationship results:
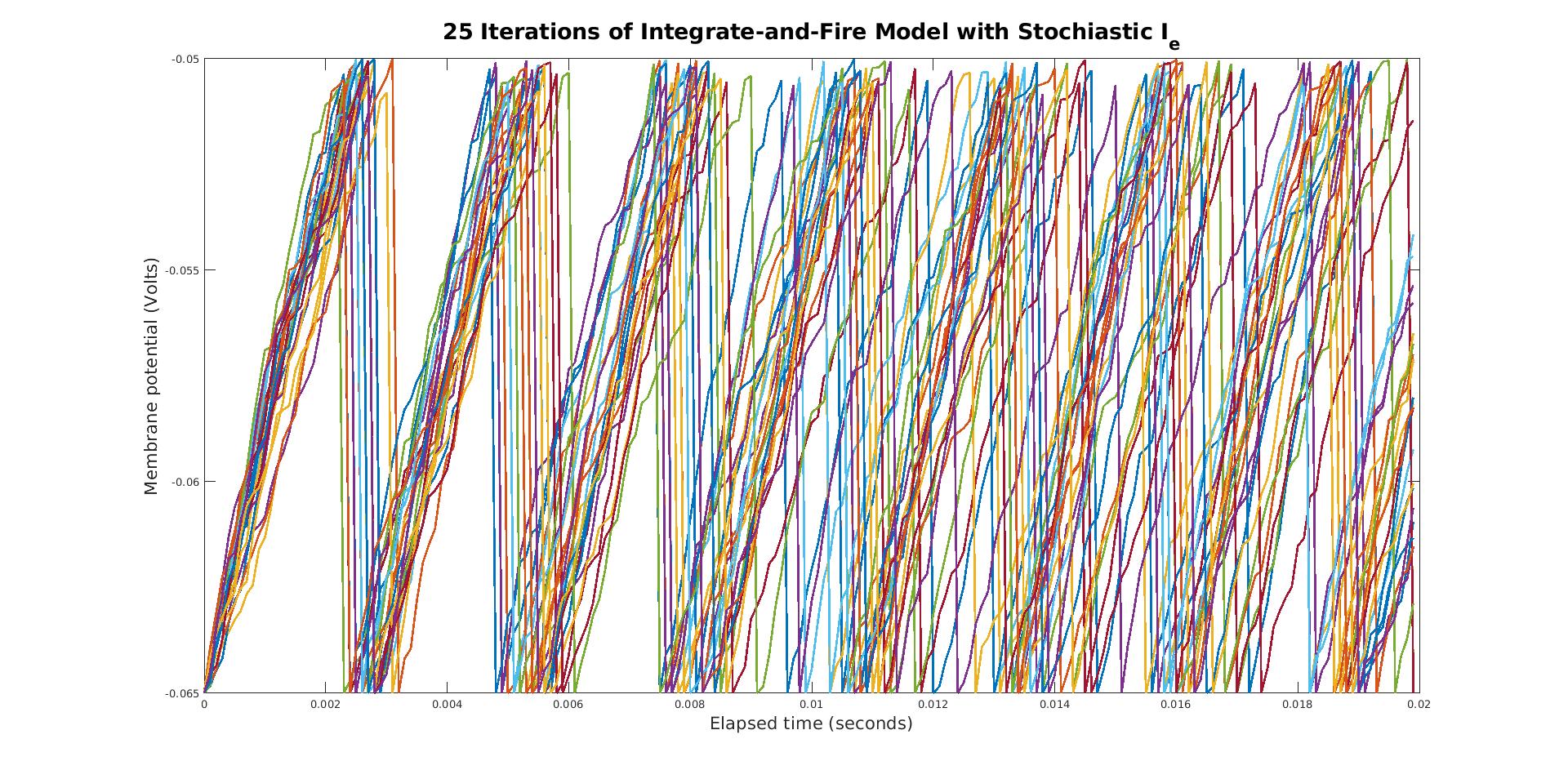
Next, we test non-constant values of I_e by once again calling integrate_and_fire and graphing the results
with plot_helper. We test both stochiastically varying and periodic values for I_e, the applied current. When
looking at a stochiastically varying I_e, we compare multiple iterations to demonstrate the effects of randomness
on firing rate and amplitude:
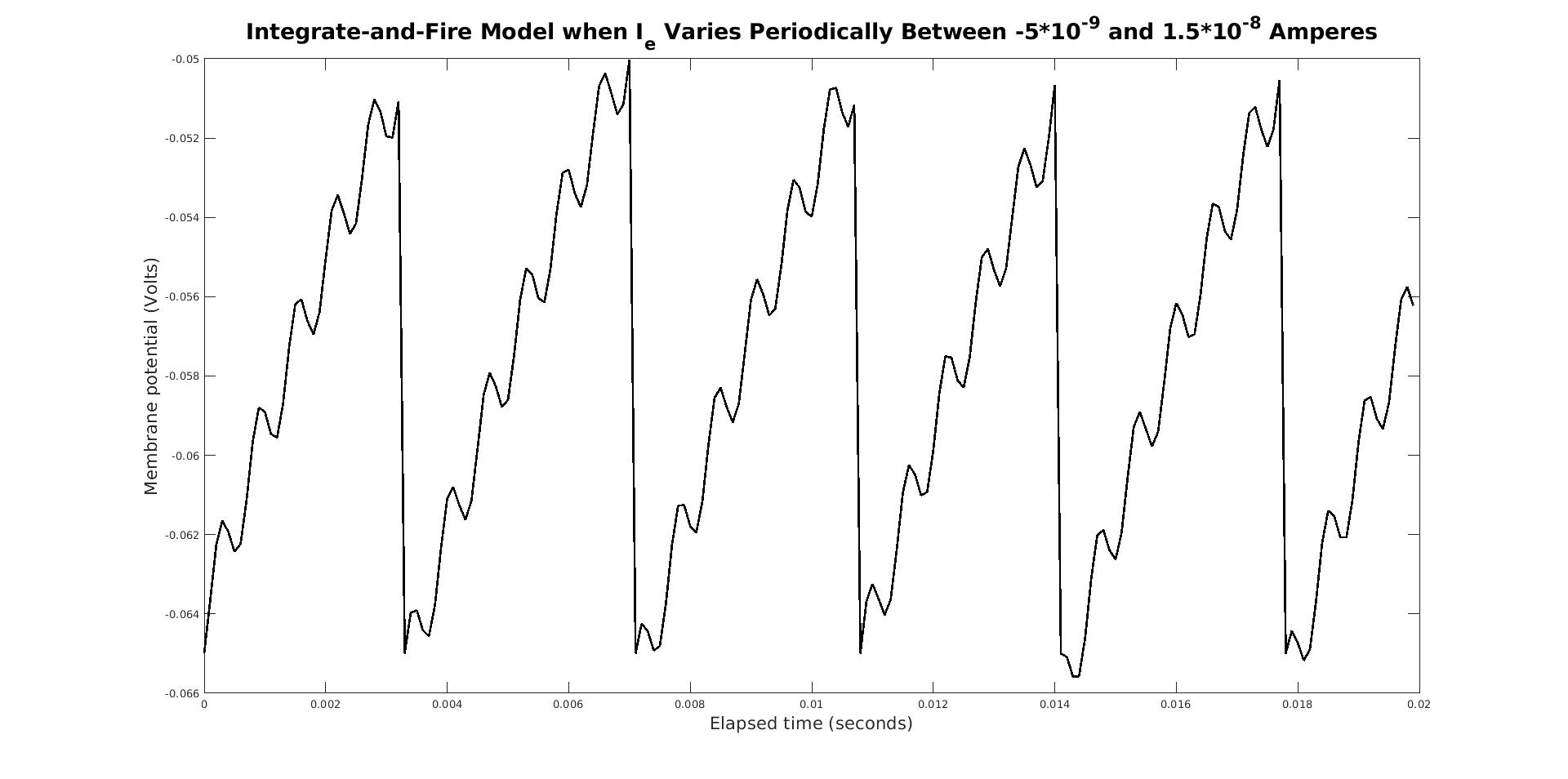
For periodic functions, no such random variation occurs, but we can clearly observe the effects of a periodic,
sin-based I_e on the membrane potential:
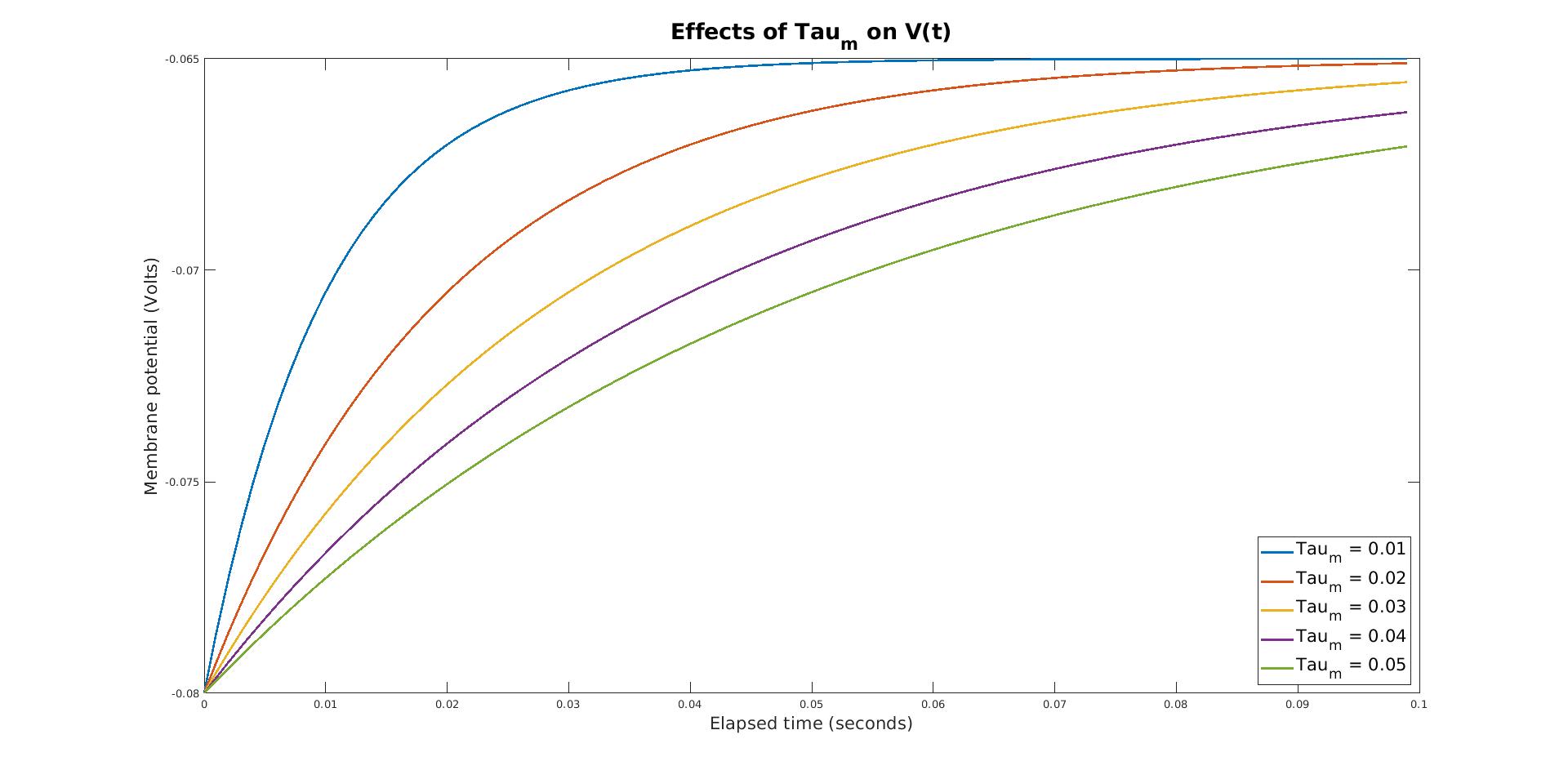
Using the solved Integrate-and-Fire differential equation as implemented in V_t, we firstly investigate the
effects of the membrane time constant, Tau_m, on the membrane potential over time. As we can see, larger values
of Tau_m lead to a slower growth of the membrane potential as it approaches the resting membrane potential.
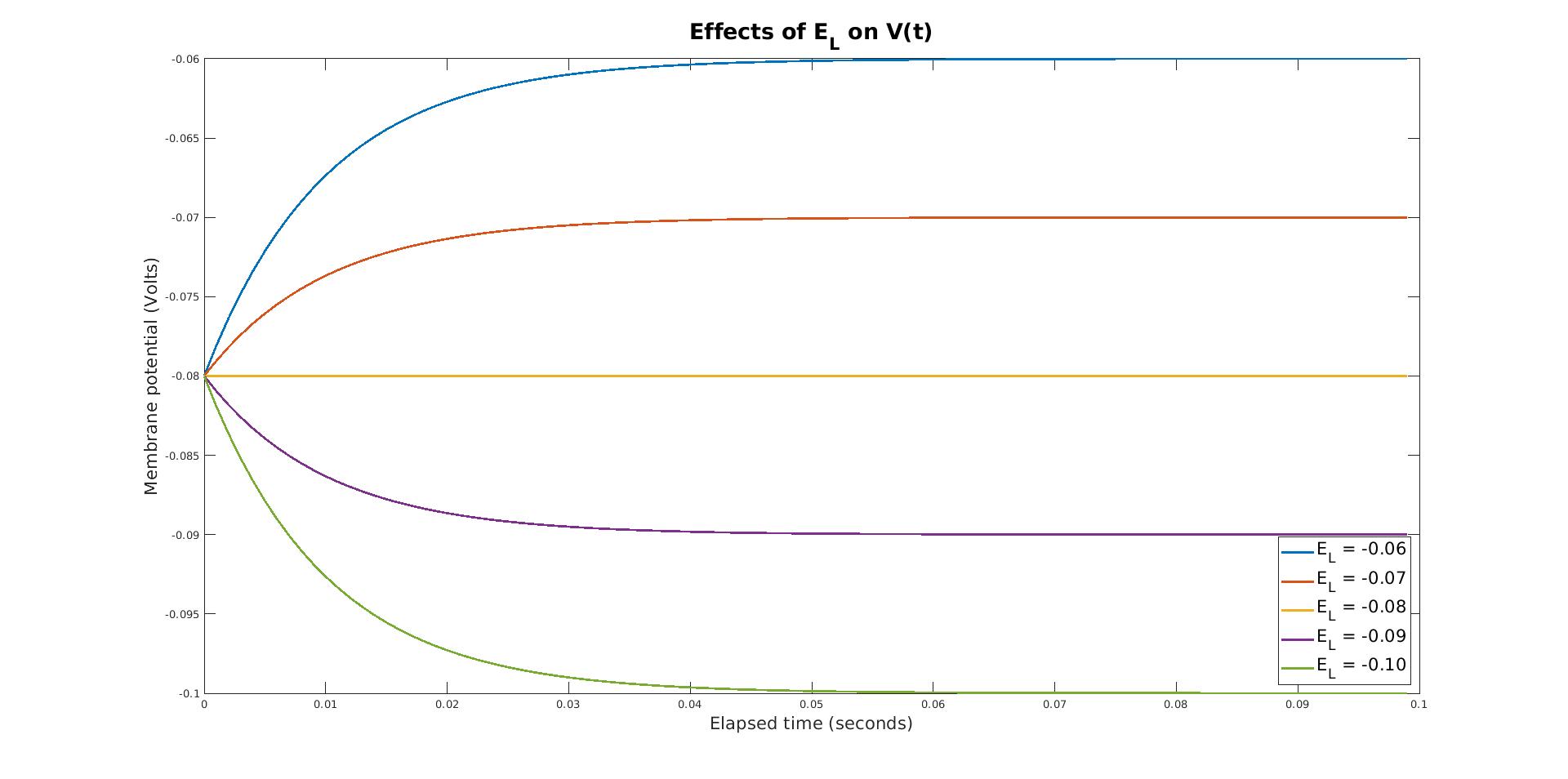
Similarly, we may investigate the effect of the resting membrane potential E_L on the membrane potential over
time. As we can see, E_L effects the point to which the membrane potential will eventually converge over time.
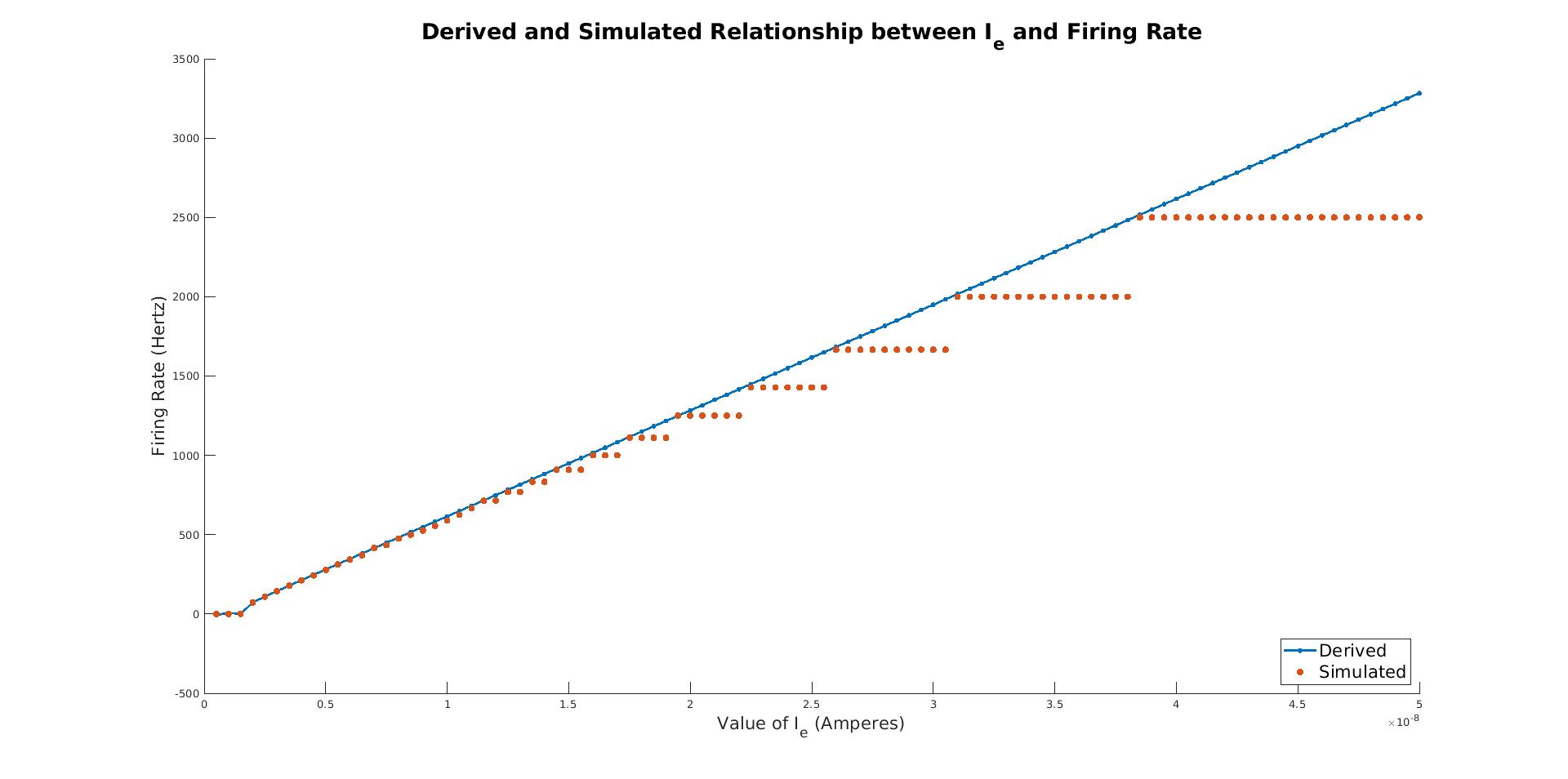
Using the derived measure of firing rate based off of the Integrate-and-Fire differential equation, we can use
theoretical_firing to compare the derived and simulated firing rate across time. As we can see below, the
derived firing rate provides an upper bound on the simulated step-wise function, and they match particularly
well for small I_e:
