coursera-pml

Practical Machine Learning with coursera

Data analysis

We begin with analysing the data manually. The training dataset contains 19.622 observations of 160 variables. The test dataset consists of 20 rows.

The output parameter is named classe and is a factor with 5 values.

> str(train$classe)
 Factor w/ 5 levels "A","B","C","D",..: 1 1 1 1 1 1 1 1 1 1 ...
> summary(train$classe)
   A    B    C    D    E 
5471 3718 3352 3147 3528

Just looking at the data, there seems to be quite a lot of empty cells and NAs. Good - we'll be able to trim down the number of colums before we actually feed the data to the training algorithms.

Another interesting observation is that every ~24 rows there seems to be some kind of a summary row copy-pasted from excel - it has string values of #DIV/0!, and in general it has very different data than the regular rows - it's marked with new_window=yes. This makes me think that it would be wise to divide the data into two parts based on the new_window column values. Furthermore we could try to build two separate models for the two parts. But for now, since it's only ~400 rows out of 19k (unnecessary clutter?), we'll skip these rows in the processing.

table(pml.training$new_window)

   no   yes 
19216   406

Column X is just an ID, so it won't be used as a feature.

Column user_name is a factor with 6 values. The assignment is about analysing whether a physical excercise is performed correctly or incorrectly, and classifying the type of errors. Although we could use this feature as the test set has exactly the same factors for this column, the algorithm shouldn't be dependent on the user_name of the person doing excercises, should be able to predict independently of who does the excercises.

table(pml.training$user_name)

  adelmo carlitos  charles   eurico   jeremy    pedro 
    3892     3112     3536     3070     3402     2610

There are three timestamp columns, that we might consider. Idea - figure out for how long the person has been excercising already - maybe there's a correlation: fatigue vs error type.

num_window seems to be some metadata related to the capturing devices. Discarding.

Now there seem to be a lot of columns related to the sensor measurements - still there's so many columns it's hard to go thru them all an filter manually. The general intuition is that we should be using features related to arms, belts, dumbbells and forearms. The rest of columns look promising for training models and running predictions.

Data preprocessing & Feature selection

We begin with the low-hanging fruits. Let's follow the intuition, let's run some naive preprocessing to clean the data, and see what kind of results we get out of it.

Regarding the cleaning - I decided to follow the approach of discarding all columns that have more than 75% empty cells (empty means '', NA or #DIV/0!). Most probably, these columns won't add much value to the final output.

y <- c("classe")
# discard features that don't seem valuable
xs <- setdiff(colnames(pml.training), c("X", "user_name", "new_window", "num_window", "raw_timestamp_part_1", "raw_timestamp_part_2", "cvtd_timestamp", "classe"))

# remove the summary rows
filterRows <- function(ds) {
  ds[ds$new_window == "no",];
}

train <- filterRows(pml.training);
test <- filterRows(pml.testing);

# drop columns that are mostly empty (NA, empty string or #DIV/0!)
mostlyEmpty <- sapply(xs, function(x) sum(is.na(train[, x]) | train[, x] == "" | train[, x] == "#DIV/0!") > 0.75 * nrow(train))
xs <- xs[!mostlyEmpty]

train <- train[,c(xs, y)]
test <- test[,c(xs)]

At this point, the numbers of potential features fell from 160 to 52. Seems like we just discarded a lot of crap :).

xs
 [1] "roll_belt"            "pitch_belt"           "yaw_belt"             "total_accel_belt"     "gyros_belt_x"        
 [6] "gyros_belt_y"         "gyros_belt_z"         "accel_belt_x"         "accel_belt_y"         "accel_belt_z"        
[11] "magnet_belt_x"        "magnet_belt_y"        "magnet_belt_z"        "roll_arm"             "pitch_arm"           
[16] "yaw_arm"              "total_accel_arm"      "gyros_arm_x"          "gyros_arm_y"          "gyros_arm_z"         
[21] "accel_arm_x"          "accel_arm_y"          "accel_arm_z"          "magnet_arm_x"         "magnet_arm_y"        
[26] "magnet_arm_z"         "roll_dumbbell"        "pitch_dumbbell"       "yaw_dumbbell"         "total_accel_dumbbell"
[31] "gyros_dumbbell_x"     "gyros_dumbbell_y"     "gyros_dumbbell_z"     "accel_dumbbell_x"     "accel_dumbbell_y"    
[36] "accel_dumbbell_z"     "magnet_dumbbell_x"    "magnet_dumbbell_y"    "magnet_dumbbell_z"    "roll_forearm"        
[41] "pitch_forearm"        "yaw_forearm"          "total_accel_forearm"  "gyros_forearm_x"      "gyros_forearm_y"     
[46] "gyros_forearm_z"      "accel_forearm_x"      "accel_forearm_y"      "accel_forearm_z"      "magnet_forearm_x"    
[51] "magnet_forearm_y"     "magnet_forearm_z"

Training model

Since it's a classification problem, not all algorithms will fit. From my previous experience (e.g. kaggle competitions) Random Forests proved to be the most efficient for classification problems - so I'll start with that.

As usual - we need to know whether our model works and what level of accuracy we can get. For this purpose we apply cross validation, partitioning the dataset at 70% training and 30% testing.

inTrain  <- createDataPartition(train[, y], p = 0.7, list=FALSE);
training <- train[inTrain, c(y, xs)];
testing  <- train[-inTrain, c(y, xs)];

model <- train(classe ~ ., data = training, method = "rf", trControl = trainControl(method="cv"), numbers=3);

predictions <- predict(model, testing);
confusionMatrix(predictions, testing[, y]);

# variable importance
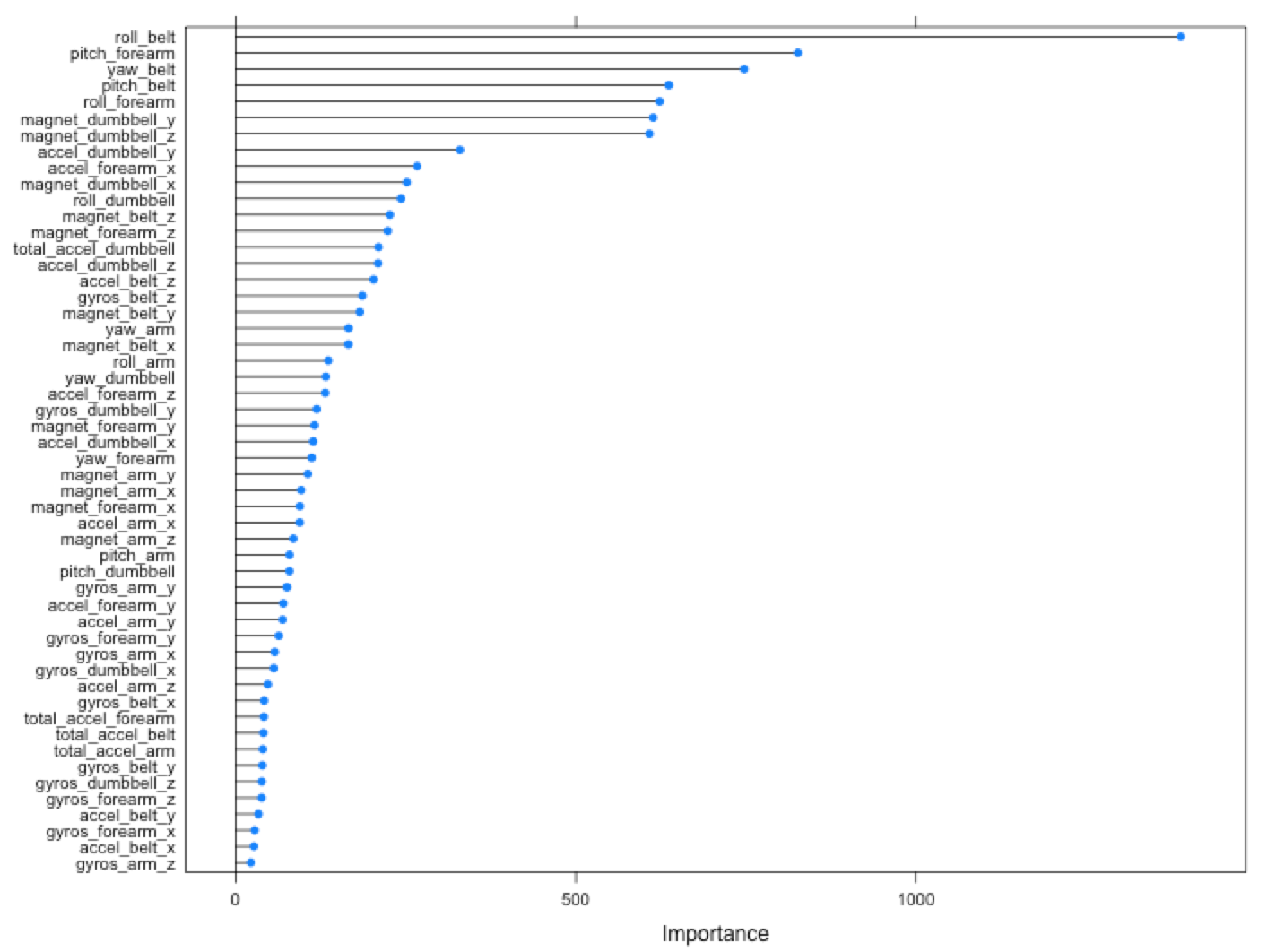
plot(varImp(model, scale = FALSE))

This gives very high accuracy already, much higher than the 'good-enough' level around 80%.

> model
Random Forest 

13453 samples
   52 predictor
    5 classes: 'A', 'B', 'C', 'D', 'E' 

No pre-processing
Resampling: Cross-Validated (10 fold) 

Summary of sample sizes: 12109, 12107, 12107, 12107, 12106, 12108, ... 

Resampling results across tuning parameters:

  mtry  Accuracy   Kappa      Accuracy SD  Kappa SD   
   2    0.9911618  0.9888175  0.002509612  0.003176747
  27    0.9913587  0.9890679  0.002350200  0.002973651
  52    0.9849896  0.9810093  0.007077471  0.008957960

Accuracy was used to select the optimal model using  the largest value.
The final value used for the model was mtry = 27. 
>
> model$finalModel

Call:
 randomForest(x = x, y = y, mtry = param$mtry, numbers = 3) 
               Type of random forest: classification
                     Number of trees: 500
No. of variables tried at each split: 27

        OOB estimate of  error rate: 0.71%
Confusion matrix:
     A    B    C    D    E class.error
A 3823    4    1    0    2 0.001827676
B   17 2577    9    0    0 0.009988475
C    0    9 2330    8    0 0.007243289
D    0    1   31 2169    2 0.015433500
E    0    0    4    8 2458 0.004858300

Confusion matrix:

> cm
Confusion Matrix and Statistics

          Reference
Prediction    A    B    C    D    E
         A 1638    6    0    0    0
         B    3 1098    5    0    0
         C    0    5  997   22    3
         D    0    6    3  922    3
         E    0    0    0    0 1052

Overall Statistics
                                          
               Accuracy : 0.9903          
                 95% CI : (0.9874, 0.9927)
    No Information Rate : 0.2847          
    P-Value [Acc > NIR] : < 2.2e-16       
                                          
                  Kappa : 0.9877          
 Mcnemar's Test P-Value : NA              

Statistics by Class:

                     Class: A Class: B Class: C Class: D Class: E
Sensitivity            0.9982   0.9848   0.9920   0.9767   0.9943
Specificity            0.9985   0.9983   0.9937   0.9975   1.0000
Pos Pred Value         0.9964   0.9928   0.9708   0.9872   1.0000
Neg Pred Value         0.9993   0.9963   0.9983   0.9954   0.9987
Prevalence             0.2847   0.1935   0.1744   0.1638   0.1836
Detection Rate         0.2842   0.1905   0.1730   0.1600   0.1825
Detection Prevalence   0.2853   0.1919   0.1782   0.1621   0.1825
Balanced Accuracy      0.9984   0.9915   0.9929   0.9871   0.9972

Other algorithms

Later on I ran a bunch of tests with other models and parameters, e.g.:

Random Forests with PCA preprocessing,
R-Part with PCA
LDA2 with PCA
PAM with PCA

But none of them yields results as good as the pure rf. So, I'll stick with that.

Variable importance

Variable importance plot shows that row_belt, pitch_forearm, yaw_belt and pitch_belt have the most impact on the predictions.

Out of pure curiousity, I ran the training and predictions taking into consideration only 7 the most influential features:

xs <- c("roll_belt", "pitch_forearm", "yaw_belt", "pitch_belt", "roll_forearm", "magnet_dumbbell_y", "magnet_dumbbell_z")

Interestingly, the accuracy on CV turned out to be 98%, which is 1% less than with all 52 features.

Conclusion

I seem to have got very decent results just by following the intuition and keeping things as simple as possible. At the beginning, when I was manually going through the data and analysing, I had a couple of ideas in the back of my head - e.g. including the rows with new_window=yes as a separate model, adding a fatigue feature (based on time passed since the beginning of excercising), but in the end I managed to get 99% estimated accuracy (based on cross validation) without actually implementing any of that.

pawelrychlik / coursera-pml