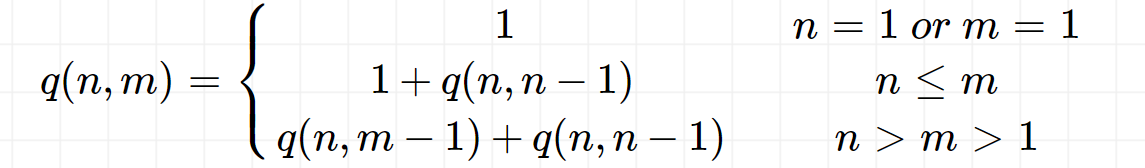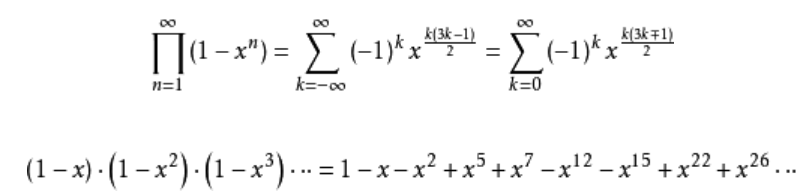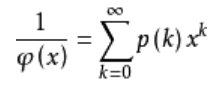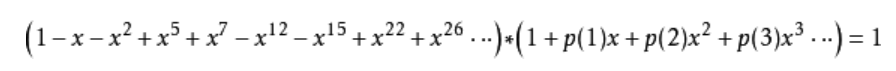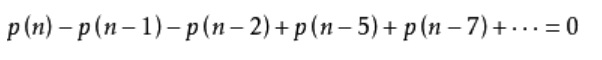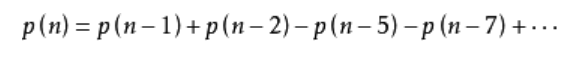组合数学作业:整数拆分
作者:张文喆 1551719
输入一个数值x,输出x的拆分数p(x)
拆分数的计算没有明晰的公式可以套用,通过查阅资料,我了解到具体的实现方法有:
- 递归法
- 动态规划
- 母函数法
- 五边形数定理
我只实现了这四个方法。
Python
这是考虑到Python优秀的科学计算能力。因为拆分数可能会很大,远远超出了C和C++中内置的整数类型的计数范围,如p(2000) = 4720819175619413888601432406799959512200344166,不利于进行处理;而Python则没有这样的麻烦。
递归方法的核心是递归表达式。在这里我规定:
- n = m1 + m2 + m3 + ... + mi (mi为正整数,且1<=mi<=n)
- max{m1, m2, m3, ..., mi} <= m
则称{m1, m2, m3, ..., mi}为整数n的一个m划分,划分的个数记为q(n, m)。
容易理解:p(x) = q(x, x)。
对于q(n, m),考虑以下事实:
- 当n = 1时,不论m取何值,都有q(1, m) = 1,即{1}
- 当m = 1时,不论n取何值,都有q(n, 1) = 1,即{1, 1, ..., 1}(共n个1)
- 当n < m时,由于划分中不可能出现负数,故q(n, m) = q(n, n)
- 当n = m时,分为两种情况讨论:
a. 当划分中包括m时,则划分情况只可能为{m}
b. 当划分中不包括m时,此时的划分情况等价于n的一个(m-1)划分
所以,q(n, n) = 1 + q(n, n-1) - 当n > m时,同样分为两种情况讨论:
a. 当划分中包括m时,则划分情况为{m, m1, m2, ..., mi},且m1 + m2 + ... + mi = n - m,所以{m1, m2, ..., mi}相当于(n-m)的一个m划分,划分数为q(n-m, m)
b. 当划分中不包括m时,划分情况等价于n的一个(m-1)划分,划分数为q(n, m-1)
综上,q(n, m) = q(n-m, m) + q(n, m-1)
运用到递归过程中,可以这样设计:1和2是递归的返回条件;3可以合并到4中;4是5的一个特殊情况,但是如果将4和5合并,需要补充条件q(0, m)=1,所以在实践中并没有将4和5合并。最终表达式为:
实际代码如下
def recursion_drive(self):
"""使用递归的方法找到拆分数,速度慢,占用栈空间大"""
num = self.x
return self.recursion(num, num)
def recursion(self, n, m):
"""具体的递归函数"""
if n is 1 or m is 1:
return 1
elif n <= m:
return self.recursion(n, n-1)+1
else:
return self.recursion(n, m-1)+self.recursion(n-m, m)可以看到,递归是一种极慢的方法,对于P(x)=q的计算,它实际上进行了q次+1运算。
递归方法速度极慢,且占用大量栈空间,所以考虑使用动态规划的方法来优化时间和空间复杂度。这里面应用的仍然是递归表达式,只不过我们将计算q(n, n)过程中的计算结果保存起来,同时不再采用递归的倒序形式,而是从小到大计算出计算出q(i, j) (0 < i < n,0 < j < m)。
设我们现在正在计算p(x),那么为了实现动态规划的效果,我们需要维护一个x*x的表,在里面填写不同n和m下的q(n, m)。而动态规划节省时间的关键在于,当我们计算q(n, m)时,将其拆分为q(n-m, m) + q(n, m-1),而q(n-m, m)和q(n, m-1)的值都已经记录在相应的位置上了,直接取用即可。最后我们返回q(n, n)的值作为p(x)。
在实践中,略有些棘手的地方在于,数组(在Python中是List)的索引由0开始,所以在计算下标时不得不进行一些变换,在阅读代码时不免令人费解。
实际代码如下
def dynamic(self):
"""使用动态规划的方法找到拆分数,速度快,占用空间大"""
num = self.x
tablet = [[0 for m in range(num)] for n in range(num)] # 构建动态规划表格
for n in range(num):
for m in range(num):
if n is 0 or m is 0:
tablet[n][m] = 1
elif n <= m:
tablet[n][m] = tablet[n][n-1]+1
else:
tablet[n][m] = tablet[n][m-1]+tablet[n-m-1][m]
return tablet[-1][-1]由于在构建动态规划用到的表格时,需要开辟x*x的数组,所以占用内存空间比较大,但是避免了占用过多的栈空间。
动态规划可以视为递归方法的优化,其核心**没有变化,而母函数方法是一种原理完全不同的方法,也是我们在组合数学课上学到的方法。
考虑整数n的所有拆分中,所有的拆分得到的数字mi都小于等于n,而在每一组拆分中,m1 + m2 + m3 + ... + mi = n,所以可以使用母函数的方法来计算拆分数,具体方法如下:
规定g(x, i)为i在x的拆分情况中的出现情况,而i出现k次表示为x^(i*k),所以g(x, i) = 1 + x^i + x^(2i) + .. + x^(k*i),且n-i < k*i <= n,这表示i在拆分中出现0, 1, 2, ..., i次。
所以G(x) = g(x, 1)g(x, 2)...g(x, n)
展开后为:G(x) = a0 + a1x + a2x^2 + .. + anx^n + ...
x^n代表一组数字的和为n,而我们的目标就是求出x^n的系数an,它就是n的拆分数p(n),也即q(n, n)。这在程序中被转化为多项式乘法的问题。
实现多项式乘法较为简单,我们只需要开辟两个长度为x的数组用于记录两组多项式的系数,然后逐位相乘,记录相乘的结果即可。在这个问题中,我们有n个多项式相乘,而且所有多项式中每一项的系数都为1,所以采用的方法是:先由g(x, 1)开始,将它记录在第一个数组中,数组中每一项都是1;然后将第一个数组中的每一项与g(x, 2)相乘,并将中间结果记录在第二个数组中,在完成两者相乘后将结果写入第一个数组。如此循环,直至n个多项式相乘完毕。
实际代码如下
def generating(self):
"""使用母函数的方法找到拆分数,速度快,占用空间小"""
num = self.x
# 两个多项式相乘,poly1存放最终结果,poly2存放中间结果
poly1 = [1 for i in range(num+1)] # 现在代表g(x, 1)
poly2 = [0 for i in range(num+1)]
for i in range(2, num+1): # g(x, i)中i的范围:[2, num]
for j in range(num+1): # 遍历poly1中的每个项
for k in range(0, num+1-j, i):
# 对于poly1中给定的幂j,g(x, i)中提供的项的幂不得超过num-j
poly2[k+j] += poly1[j] # 幂为k+j的项的系数增加1*poly1[j]
poly1 = poly2 # 将poly2中的计算结果转存到poly1中
poly2 = [0 for i in range(num+1)]
return poly1[num]母函数方法占用的空间较小,但是运行速度略微不如动态规划。
为了使用这种方法,我们必须首先了解五边形数和欧拉函数。
五边形数是能排成五边形的多边形数。第 n个五边形数可用以下公式求得:
pn = (3n^2-n) / 2 , n > 0
示意图如下:
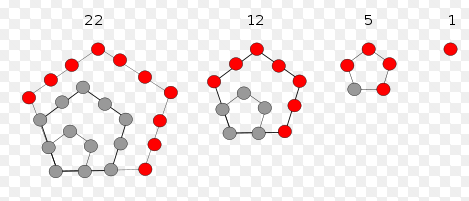
现在引入广义五边形数:允许n <= 0即可,公式保持不变。
又,五边形数被用于描述欧拉函数展开式的特性。欧拉函数展开如下:
注意到展开式的最终结果,留下来的非零次项的幂即广义五边形数。
现在引入欧拉函数和分割函数(即p(n))的关系:由3. 母函数模块知,拆分函数的母函数恰为欧拉函数的倒数,具体推导过程省略。
我们主要关心x^n项的系数。根据等号左右两边式子的关系,这个系数应为0,即:
得到这个递推关系式后,我们将其与动态规划的方法相结合,由p(1)一直计算到p(n)。
由此,我们借助欧拉函数作为桥梁,将广义五边形数与拆分函数联系了起来。这样做的好处在于:拆分数没有明晰的表达式,只有递推关系,这导致计算速度很慢;而广义五边形数有明确的计算公式,借助这个公式,我们拿到了p(n)的相对简洁得多的递推关系式,这大大减少了我们的计算量。
实际代码如下
def pentagonal_number(self):
"""使用五边形数定理计算拆分数,速度快,占用空间小"""
num = self.x
# 构建辅助数组
assist = []
for i in range(1, num):
assist.append(int(i*(i*3-1)/2))
assist.append(int(i*(i*3+1)/2))
# 构建由1~num的拆分数列表
p_list = [1, 1, 2]
for i in range(3, num+1):
count = 0
p = 0
for j in range(0, i):
if assist[j] > i:
break
count %= 4
if count is 0 or count is 1:
p += p_list[i-assist[j]]
else:
p -= p_list[i-assist[j]]
count += 1
p_list.append(p)
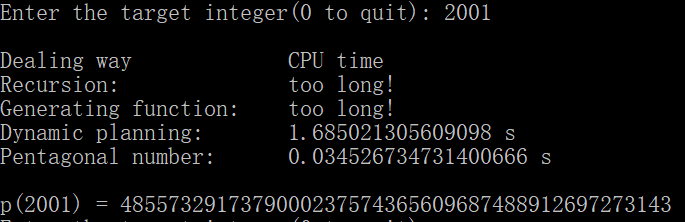
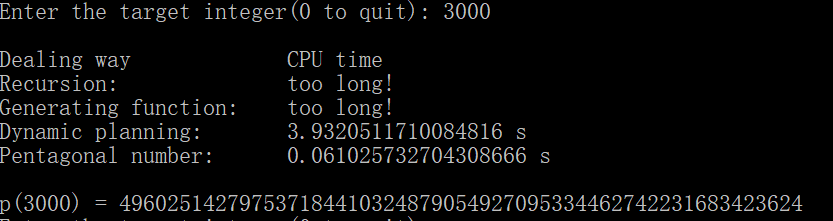
return p_list[num]这种方法比纯动态规划的方法要快得多,它的时间复杂度为O(n^1.5),而纯动态规划方法的时间复杂度为O(n^2);并且它占用更小的空间,空间复杂度为O(n),纯动态规划方法的空间复杂度为O(n^2)。具体对比可以参考下面x=3000时的运行速度。
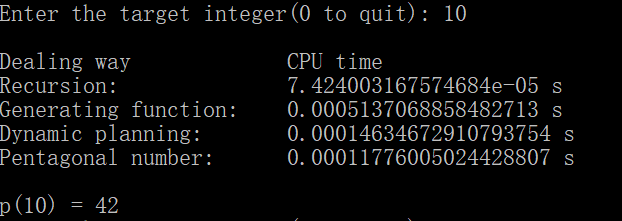
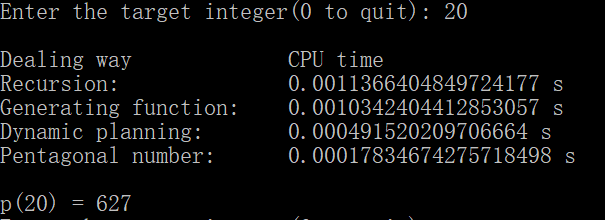
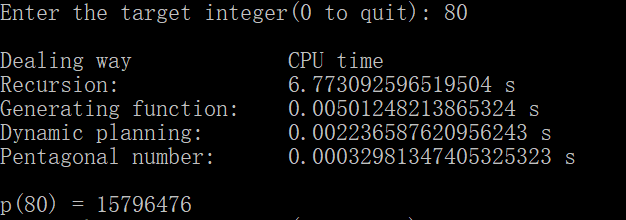
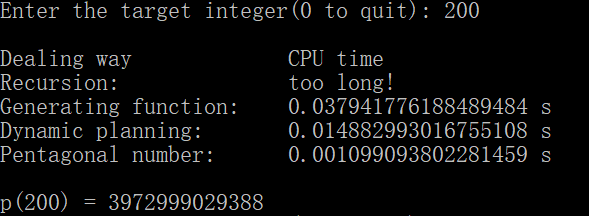
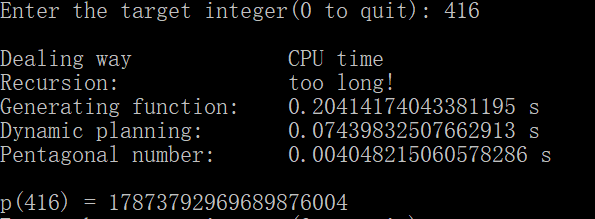
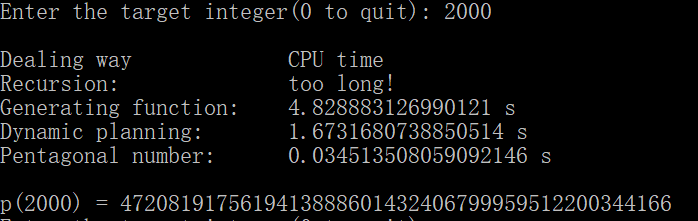
为了避免递归方法运行时间太长,阻塞程序,所以我规定,当x > 80时,不再执行递归方法。当x大于一定数值时,母函数方法也会变慢,所以当x > 2000时,不再执行母函数方法。当x > 3000时,不再执行动态规划方法。四种方法的运行效果如下,列表从上到下依此为递归方法、母函数方法、动态规划方法和五边形数定理方法:
可以看到,随着x的增大,p(x)增长得越来越快。
另外值得一提的是,为了保证四种方法得到的结果不会出现偏差,我对它们的结果进行了验证,保证其准确性:
for result in result_list:
assert p4 == result, 'wrong answer!'经过检验,并没有出现错误。
我在电影《知无涯者》中看到麦克马洪手算了前200个整数的拆分数,在观影时我并没有在意这个细节,但是知道我今天真的算出了p(200) = 3972999029388,我才意识到每个时代的数学家都有着自己的伟大之处。
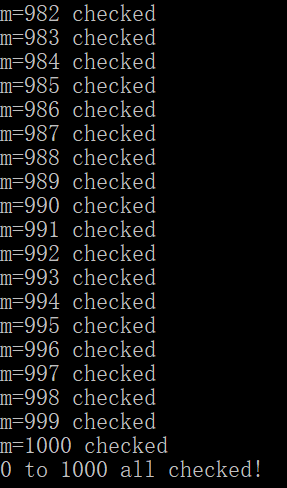
除此之外,据说拉玛努金发现,p(5m+4)可以被5整除,p(7m+5)可以被7整除,p(11m+6)可以被11整除,我对此进行了验证,发现至少对于我目前能够计算到的范围都是成立的。程序运行的部分截图如下:
代码如下
def main():
max_m = 1000
p_list = pentagonal_number(11*max_m+6)
for m in range(0, 1001):
p = p_list[5*m+4]
assert p % 5 == 0, '5*{}+4 failed!'.format(m)
p = p_list[7*m+5]
assert p % 7 == 0, '7*{}+5 failed!'.format(m)
p = p_list[11*m+6]
assert p % 11 == 0, '11*{}+6 failed!'.format(m)
print('m={} checked'.format(m))
print('{} to {} all checked!'.format(0, max_m))向拉马努金、哈代和麦克马洪致敬。