Topos

This library implements natural topological and combinatorial operators on statistical networks described in [1] and [2] They for instance yield message-passing algorithms on graph neural networks, the belief propagation (BP) or sum-product algorithm for efficient marginal estimation (generalised to hypergraphs in [3]), and the belief diffusions that regularise BP [2].

The main data structure consists of fields of tensors, each having possibly different shapes, and stored internally as 1D Pytorch vectors. They can be for instance indexed by the hyperedges of a hypergraph $K \subseteq \mathcal{P}(\Omega)$, i.e. a collection of regions $\mathrm{a} \subseteq \Omega$ describing which variables are allowed to be measured simultaneously. In the case of a graph of binary variables, a field $(f_{\mathrm{a}})$ maps each vertex $i$ to a tensor $f_i$ of shape [2] (a function on $\lbrace{-1, +1 \rbrace}$) and each edge $ij$ to tensor $f_{ij}$ of shape [2, 2] (a function on $\lbrace -1, +1 \rbrace^2$).

This kind of structure may be called a spin glass in physics, a Hopfield network in neuroscience, or a Boltzmann machine or energy-based model in artificial intelligence, all of which are essentially equivalent to the famous Ising model.

Degree-0 fields are therefore collections of local functions $(f_{\tt a})$ for ${{\tt a \in }K}$, whose sum over $K$ is typically used to parameterise a global energy function (while such a global observable may be evaluated quickly, computing integrals or expectations is intractable in high dimension). Higher-degree fields for instance describe the degree-1 messages $m_{\mathrm{a \to b}}$ which are iterated upon in the belief propagation algorithm (for marginal estimation) or in message-passing neural networks (MPNNs). They are indexed by ordered region pairs $\mathrm{a \supset b}$ which generate the nerve of $K$ [2].

References

[:book:] : The topos wiki

[1] : Peltre, 2020, Message-Passing Algorithms and Homology, PhD thesis. arXiv:2009.11631

[2] : Peltre, 2021, Belief Propagation as Diffusion. GSI'21 proceedings. arXiv:2107.12230

[3] : Yedidia, Freeman and Weiss, 2000 - Generalized Belief Propagation, NeurIPS 2000. full text

Usage

Installation

Run pip install git+https://github.com/opeltre/topos

Or clone the repository locally before installing:

$ git clone https://github.com/opeltre/topos
$ cd topos
$ pip install .

You should be able to run tests with:

$ cd test && python -m unittest

Interfacing with Pytorch

The main purpose of this library is to construct various (wrapped) Pytorch tensors, related to the topology of an underlying data structure (graph, hypergraph, simplicial complex...). These tensor either represent fields of values over a domain (dense vectors, wrapped in the Field class), or linear operators between field types (sparse matrices, wrapped in the Linear class).

Working with these two classes has little more overhead than storing a reference to underlying domains, while providing a few convenient methods (e.g. f @ g for calling torch.sparse.matmul and f @ x for calling torch.sparse.matvec). Either way, the underlying Pytorch tensor may be accessed by the .data attribute, for seamless interfacing with other Pytorch or Pytorch-geometric code.

class GCN(nn.Module): 
     """ Glass Convolutional Network """

     def __init__(self, G, num_filters=10, degree=3):
          self.graph   = topos.Complex(G)
          self.weights = nn.Parameter(torch.randn(num_filters, degree))
          #--- Powers of the graph laplacian --- 
          L = self.graph.laplacian(0)
          self.L_powers = [self.graph.eye(0)]
          for i in range(degree):
               self.L_powers.append(L @ self.L_powers[-1])


     def forward(self, x):
          X = self.graph[0].field(x)
          #--- Convolutional filters are polynomials of the laplacian --- 
          P_L = sum(wk * Lk for wk, Lk in zip(self.weights, self.L_powers))
          return (P_L @ X).data

>>> V = torch.arange(12)
>>> E = torch.randint(12, (10, 2))
>>> gcn = GCN([V, E])
>>> x = torch.randn([100, 12])
>>> y  = gcn(x)

The mechanism for wrapping and typing Pytorch tensors has been moved to an other repository, opeltre/fp. Its purpose is to provide generic functorial constructs to emulate type polymorphism in Python. It exposes an unsafe Tensor class, a typed Tens : Shape -> Type functor, a Linear bifunctor... all holding a torch.Tensor instance wrapped inside an fp.Tensor instance (algebraic methods are lifted from one type to the other by a Wrap monad).

Contributing

Contributions are welcome. I am already grateful to @aklipfel for helping in the sparse module to speed up some of the index computations dramatically. If you enjoy this library and would like to help in any way please get in touch.

Overview

Fields and Domains

Index ranges are represented by topos instances subclassing the Domain base class. The Field functor then maps any domain D to a tensor type Field(D) wrapping 1D-torch vectors of length D.size:

from topos import Domain, Field
#--- Domain with keys [0, ..., n-1]
D = Domain(list(range(n)))
#--- Tensor type of shape [n] ---
FD = Field(D)  
#--- Fields wrap torch tensors ---
x  = FD(torch.zeros([n]))
True == isinstance(x.data, torch.Tensor)

A field instance x = D.field(data) can be created from any numerical data of the appropriate size. Note that D also provides with common fields constructors such as D.zeros(), D.ones(), D.randn(), etc.

Sheaves

The Sheaf class is a generic base class representing finite domains defined as a dependent sum type:

$$ F(K) = \bigsqcup_{a \in K} F_a $$

i.e. points of $F(K)$ are key-value pairs $(a, x_a)$ for $a$ in a set of keys $K$ and $x_a$ in the finite set $F_a$. A trivial sheaf, i.e. with a point above each key, is constructed by default. No categorical structure is assumed on $K$ so that one may create a non-trivial Sheaf instance by supplying shapes above each key by a list of shapes, a callable, or aggregate keys and shapes in a dictionnary.

from topos import Sheaf

#--- Sheaf(keys, functor=None) : equivalent forms ---
F = Sheaf({'ij': [3, 3], 'i': [3], 'j': [3]})
F = Sheaf(['ij', 'i', 'j'], lambda k: [k] * len(k))
F = Sheaf(['ij', 'i', 'j'], [[3, 3], [3], [3]])

The cardinal F.size of a sheaf instance F can be computed as:

F.size = sum(F(a).size for a in F.keys)
       = sum(Fa.size for Fa in F.fibers)

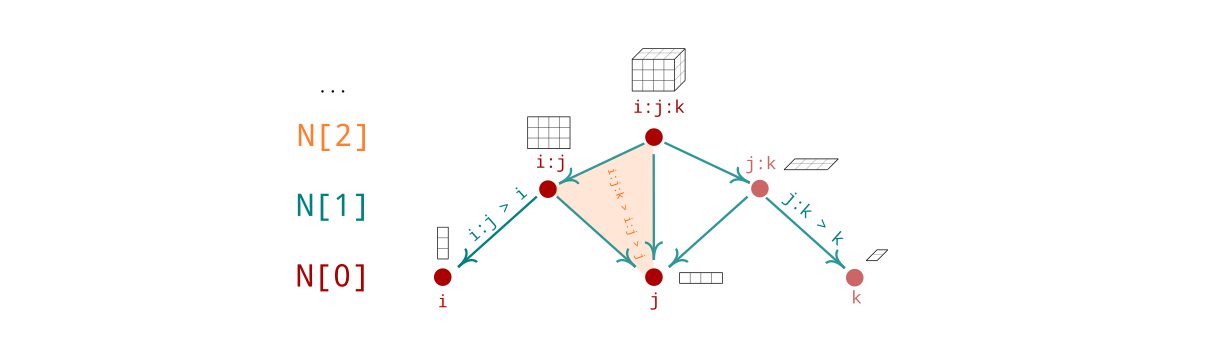
The corresponding index map for Field(F) instances can be conveniently visualized by calling F.range():

>>> F.range()
Field Ω :  ij :        [[0, 1, 2],
                        [3, 4, 5],
                        [6, 7, 8]]
           i :        [ 9, 10, 11]
           j :        [12, 13, 14]

(Hyper)graphs

The Graph class (which should be called Hypergraph) is a base class for sheaves G whose keys can be represented by (positive) torch.LongTensor instances of shape (len(G[k].keys), k + 1). In particular G is a graded sheaf instance with fibers G[0], ..., G[G.dim] each containing len(G[k].keys) regions of cardinal k + 1, also called hyperedges of dimension k. Instantiating large graph instances is much faster than large sheaf instances, as they enable to leverage on Pytorch's sparse matrix library.

A 1-graph G can for instance be created by:

from topos import Graph
G0 = [0, 1, 2, 3]
G1 = [[0, 1], [0, 2], [0, 3]]
G = Graph([G0, G1])

The resulting Sheaf instance has two keys 0 and 1 pointing to graded components of size G.sizes[k] and begining at G.begin[k]:

>>> G.range()
Field G :  0 :  [0] :        0
                [1] :        1
                [2] :        2
                [3] :        3
               
           1 :  [0, 1] :        4
                [0, 2] :        5
                [0, 3] :        6

A general n-graph G defines n+1 sparse adjacency tensors G.adj[k] of dimension k + 1 for k = 0, ..., n. Sparse tensors G.idx[k] of identical shapes allow for fast index access (sometimes by custom routines defined in core/sparse.py, thanks to Astrid Klipfel). This is particularly useful during the computation of topological operators when G is equipped with additional structure.

A functor-valued graph GF = Graph(G, F) can be defined given a functor F that maps (1) every region a to a shape F(a) and (2) every strict inclusion relation a > b to an index map F.fmap([a, b]). See functors for more details on functor creation. A canonical example is given by free functors, i.e. mapping every region to a cartesian product of atomic microstates.

from topos import FreeFunctor
#--- Each vertex has 3 degrees of freedom ---
F = FreeFunctor(3)
#--- Shape [3, 3] on edges ---
GF = Graph(G, F)

Simplicial complexes

The Complex class inherits from Graph and is used to represent graphs K such that for every region a in K, any subregion b of a also belongs to K. The simplest way to define a simplicial complex is via the simplicial class method:

from topos import Complex
#--- Simplicial closure ---
K = Complex.simplicial([[0, 1, 2], [1, 2, 3]])

The functor-valued simplicial complex KF associated to a functor F can then be created by:

KF = Complex(K, F)

Because the Complex constructor does not compute simplicial closures by default, be sure to provide a simplicially closed set of keys K when using the latter form.

Simplicial complex contain all the structure required for differential calculus. This means every complex defines a degree 1 linear map $d$ mapping k-fields to (k+1)-fields for all k, and satisfying the fundamental equation $d^2 = d \circ d = 0$.

d0 = K.diff(0)
d1 = K.diff(1)
# d1 @ d0 : Field K[0] -> Field K[2]
K.zeros(2) == d1 @ d0 @ K.randn(0)

When K has scalar or constant coefficients, the first differential K.diff(0) from K[0] to K[1] simply maps a function on vertices to a function on directed edges by computing differences between end points. Edge features may also to be mapped to vertex features by a given functor. Its pullback then maps vertex observables to edge observables, allowing for a differential to be defined. The fundamental example consists of the FreeFunctor mapping every region $\mathrm{a} \subseteq \Omega$ to a local cartesian product $E_{\mathrm{a}} = \prod_{i \in \mathrm{a}} E_i$.

The tranposed operator K.codiff(k+1) = K.diff(k).t() decreases degree by 1 and involves the linear adjoints of functorial maps when K is equipped with functorial coefficients (this means Field(K) is identified with its linear dual by the canonical metric of $\mathbb{R}^{\tt K.size}$). In the case of a 1-complex K, the codifferential K.codiff(1) is the discrete divergence operator, aggregating directed edge values onto source and target vertices with opposite signs.

Note that differential operators are not computed upon complex creation but cached for reuse when called for the first time instead. Calling K.diff(x) on a degree k field instance will look for the operator K.diff(k) before applying it on the input field.

#--- K.diff(0) is added to K[0]._cache ---
>>> K.diff(0)
Linear K[0] -> K[1] : d
#--- Degree 0 random field ---
>>> x = K.randn(0)
#--- Lookup for K[x.degree]._cache["d"] ---
>>> K.diff(x)
Field K[1] : ...

Nerves

Nerve instance both leverage on the simplicial structure of Complex instances on the partial order structure of the underlying Hypergraph instance.

They are best constructed by calling Graph.classify().

opeltre / topos