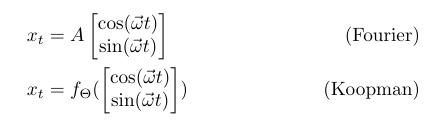Paper: [From Fourier to Koopman: Spectral Methods for Long-term Time Series Prediction (jmlr.org)](https://jmlr.org/papers/v22/20-406.html)
Fourier and Koopman constitute spectral algorithms for learning linear and non-linear oscillators from data respectively. Both algorithms solve a global optimization problem in frequency domain and allow for modeling of systems of any dimensionality. The algorithms are written in numpy and pytorch.
The objective of the algorithms is, respectively:
This code accompanies the following paper. A video abstract of the paper can be found here. Results on modeling a number of fluid flows can be found here.
Fourier fits a linear oscillator to data. The number of frequencies k that the signal is assumed to exhibit and a learning rate needs to be specified. It is recommended to whiten the signal (zero-mean and unit-variance).
To learn the oscillator from data, do:
from fourier_koopman import fourier
import numpy as np
x = (np.sin([2*np.pi/24*np.arange(5000)]) + np.sin([2*np.pi/33*np.arange(5000)])).T
x = x.astype(np.float32)
f = fourier(num_freqs=2)
f.fit(x[:3500], iterations = 1000)To perform forecasting, do:
x_hat = f.predict(5000)Because of the many different ways in which the Koopman algorithm can be utilized, running it is more involved and might require writing a custom model_object. Below we provide an example where f is a simple MLP and the squared loss is employed. In general, the class koopman is instantiated with a model object that specifies:
- the topology of f
- the loss
- the number of frequencies num_freqs
from fourier_koopman import koopman, fully_connected_mse
import numpy as np
x = np.sin(2*np.pi/24*np.arange(5000))**17
x = np.expand_dims(x,-1).astype(np.float32)
k = koopman(fully_connected_mse(x_dim=1, num_freqs=1, n=512), device='cuda:0')
k.fit(x[:3500], iterations = 1000, interval = 100, verbose=True)To perform forecasting, do:
x_hat = k.predict(5000)In the following, a more involved example is given that uses a 1D tranpose-convolutional Neural Network to learn a traveling wave.
TO DO: ADD EXAMPLE
Please see the LICENSE file.