FEMcy

a finite element solver based on Taichi, being parallel (CPU/GPU), portable and open-source

FEMcy is a finite element solver for structural analysis in continuum mechanics, powered by cross-platform parallel (CPU/GPU) computing language of Taichi. FEMcy is flexible for customized needs by open-source. The mechanism behind computational structural analysis (CSD) is now opened for you, and can be manipulated by you to meet your customized needs. We provide the implementation on GPU parallel computing, meanwhile maintain the friendly readability by Python language.

Features

both small deformation and large deformation (geometric nonlinearity) are enabled
friendly readability by Python, parallel by Taichi
material nonlinearity (customize your constitutive model)
many types of elements including second-order elements
Dirichlet boundary condition (BC) and Neumann BC are enabled

currently supported Elements

linear trianguler element (CPE3 and CPS3)
quadratic trianguler element (CPE6 and CPS6)
linear quadrilateral element (CPS4 and CPE4)
quadratic quadrilateral element (CPS8 and CPE8)
linear tetrahedral element (C3D4)
quadratic tetrahedral element (C3D10, noted: this could take 5 minutes of compile time due to large ti.Matrix)

currently supported Boundary Conditions

Neumann Boundary Condition (Surface Traction)
Dirichlet Boundary Condition (Nodal Displacement)

Installation and Usage

install Python (3.8+) and pip, then install Taichi, numpy and scipy

pip install taichi
pip install numpy
pip install scipy

git clone this project
go to the current directory of this project, and run the code by:

python ./main.py

Pre-processing: choose an .inp file (the Abaqus-input-file-format) which defines the geometry, mesh, material and boundary condition for structual analysis. The .inp file can be obtained by Abaqus pre-processing GUI. For example, insert the path and inp file name to the command line:

please give the .inp format's input file path and name: tests/beam_deflection/load800_freeEnd_largeDef/beamDeflec_quadPSE_largeD_load800.inp

more examples of inp files can be found at ./tests folder
after convergence, the deformed body colored by mises-stress (defaultly) is showed at the window.

Examples (some benchmark problems)

1. elliptic-membrane with constant pressure

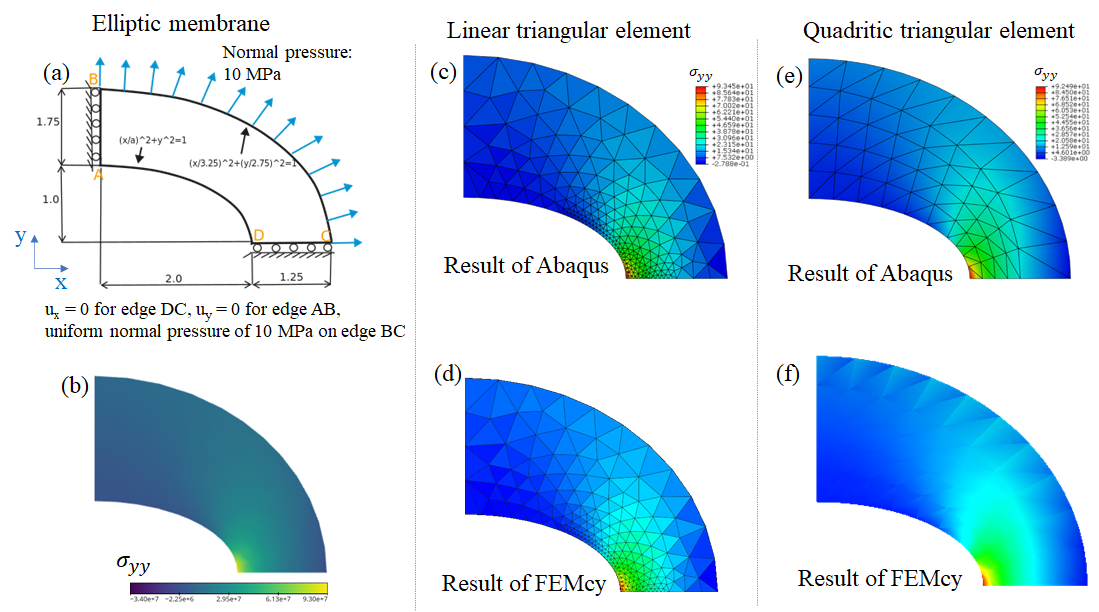
Fig. 1 shows the geometric and consititutive model definition of elliptic membrane problem, which can be refered to CoFEA benchmark. The stress $\sigma_{yy}$ at point D is expected to be 92.7 MPa.

boundary condition and loading condition

$u_{x}$ = 0 for edge DC, $u_{y}$ = 0 for edge AB, uniform normal pressure of 10 MPa on edge BC

property	value	unit
Young's modulus, E	$2.1\times10^{5}$	MPa
Poisson's ratio, $\nu$	0.3	-

Results are showed below:

Fig. 1 Results of elliptic membrane under normal pressure. (a) geometric model definition; (b) results from CoFEA; (c, d) results of linear triangular element from Abaqus and FEMcy respectively; (e, f) results of quadratic triangular element from Abaqus and FEMcy respectively, shown by nodal stress extrapolated from integration points.

Results of simulation:

$\sigma_{yy}$ [MPa] at point D	linear element	quadratic element
		$\sigma_{yy}$ at node (extrapolated)	$\sigma_{yy}$ at integration point
Abaqus	93.45	93.34	84.42
FEMcy	93.56	93.32	84.40
relative error	0.12%	0.021%	0.024%

The relative error shown above is the error between results of Abaqus and FEMcy, indicating that the results of these two softwares are almost the same.

Another interesting point is that, the linear element needs a very locally-refined mesh to get close to the expected result (~ 92.7 MPa), whereas the quadratic triangular element can get the accurate result at a relative coarse mesh as shown in the above figure.

corresponding .inp file:

linear element:

./tests/elliptic_membrane/element_linear/ellip_membrane_linEle_localVeryFine.inp

quadratic element:

./tests/elliptic_membrane/element_quadratic/ellip_membrane_quadritic_trig_neumann.inp

results can be compared with https://cofea.readthedocs.io/en/latest/benchmarks/004-eliptic-membrane/model.html

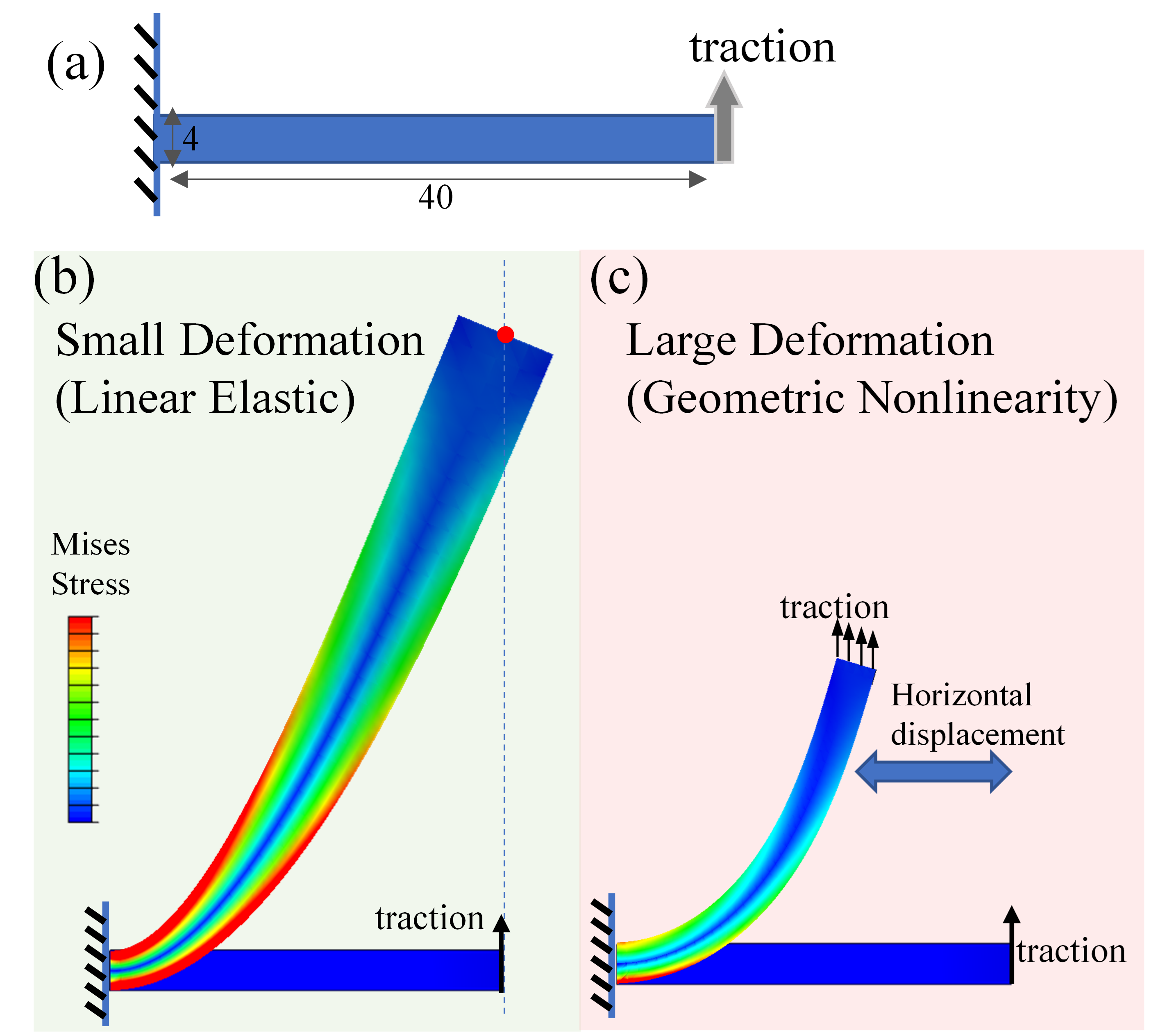
2. Beam Deflection (comparison of small and large deformation)

For a cantilever beam as shown in Fig. 2, when imposing surface traction at the free end, the results show great differences between small and large deformation.

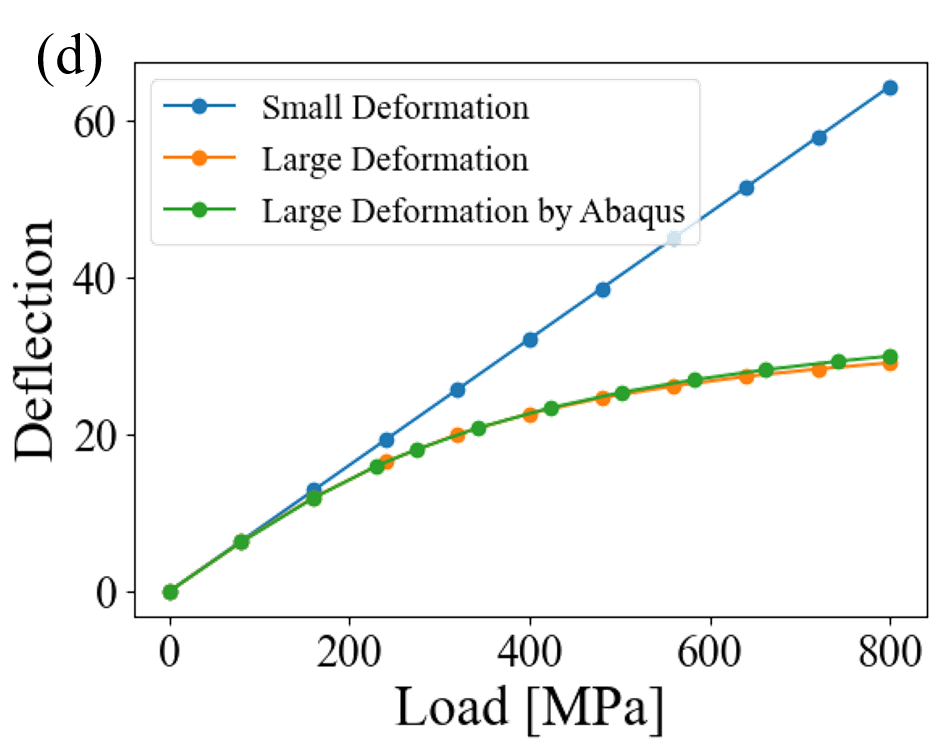
Small deformation (linear elastic) has no horizontal displacement at the free end, whereas large deformation (geometric nonlinear) shows a bending beam with horizontal displacement at the free end. Curves of vertical deflection vs. load are shown in Fig. 2 (d), which shows that the geometric nonlinear case has nonlinear deflection-load relation, and results of FEMcy are pretty close to Abaqus.

Results of large deformation (geometric nonlinear) is computed by Newton's method with adaptive time step and relaxation factor, where the Jacobian matrix $\partial\ nodal\ force\ /\ \partial\ nodal\ displacement$ at each Newton-step is approximated by the stiffness matrix [K].

Fig. 2 (a) Cantilever Beam, with surface traction at the free end. (b) Linear elastic case has no horizontal displacement at the free end, whereas (c) geometric nonlinear case shows a bending beam with horizontal displacement at the free end. (d) Curves of vertical deflection vs. load

.inp file for small deformation

tests/beam_deflection/load800_freeEnd_smallDef/beamDeflec_quadPSE_largeD_load800.inp
.inp file for large deformation

tests/beam_deflection/load800_freeEnd_largeDef/beamDeflec_quadPSE_largeD_load800.inp

(The material here has 2.e5 MPa of Young's modulus and 0.3 of Poisson's ratio)

3. Twist Plate

Run Python main.py and then insert the .inp file tests/twist/twist_plate_C3D4.inp or tests/twist/twist_plate_C3D10.inp to the command line.

The results are shown in Fig. 3 with both linear and quadratic tetrahedral elements. You can see that at the cross section perpendicular to rotation axis, stress is higher at the outer edge with larger radius at the cross section, which agrees well with the classical torsion problem.

C3D4 linear Tetrahedral	C3D10 quadratic tetrahedral

Fig. 3 Twist plate with C3D4 and C3D10 element respectively, colored by Mises stress.

Future work

accelerate by MeshTaichi.
more types of boundary conditions, such as periodic-boundary-condition (PBC) by Lagrangian-multiplier method is on-going
multiphysics, general PDE solver
dynamic analysis
flexible adaptive-mesh (local-refinement dynamically)
contact and friction by penalty method (such as IPC) or Lagrange multiplier method.
support more file-formats for pre-processing, such as Ansys input file format. Or even develop a pre-processing GUI for you to define the geometry, mesh, material, boundary conditions, etc.
support more sophisticated post-processing of the output data, such as output VTK file for ParaView visulization.

References

An Introduction to the Finite Element Method https://www.comsol.com/multiphysics/finite-element-method
FEM vs. FVM https://www.comsol.com/blogs/fem-vs-fvm/
What Is Geometric Nonlinearity? https://www.comsol.com/blogs/what-is-geometric-nonlinearity/
Abaqus documentation http://130.149.89.49:2080/v6.14/
Taichi documentation https://docs.taichi-lang.org/docs/
Claes Johnson, Numerical solutions of PDEs by finite element method https://cimec.org.ar/foswiki/pub/Main/Cimec/CursoFEM/johnson_numerical_solutions_of_pde_by_fem.pdf
Preconditioned conjugate gradient method https://www.cs.cmu.edu/~quake-papers/painless-conjugate-gradient.pdf, page 40
Solution techniques for non-linear finite element problems https://onlinelibrary.wiley.com/doi/epdf/10.1002/nme.1620121106
Taichi courses of deformable objects https://www.bilibili.com/video/BV1eY411x7mK?spm_id_from=333.337
awesome examples of other simulation methods from awesome-taichi https://github.com/taichi-dev/awesome-taichi

mo-hanxuan / FEMcy