%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import math
class ResNet3:
INsize = 1
HD1size = 1
HD2size = 1
OUTsize = 1
W1 = [[0]]
W2 = [[0]]
Wres = [[0]]
Wout = [[0]]
B1 = [0]
B2 = [0]
B3 = [0]
def ReLu(self,x):
mask = (x>0) * 1.0
return mask *x
def d_ReLu(self,x):
mask = (x>0) * 1.0
return mask
def tanh(self,x):
return np.tanh(x)
def d_tanh(self,x):
return 1.0 - self.tanh(x)**2
def softmax(self, X, theta = 1.0, axis = None):
"""
Compute the softmax of each element along an axis of X.
Parameters
----------
X: ND-Array. Probably should be floats.
theta (optional): float parameter, used as a multiplier
prior to exponentiation. Default = 1.0
axis (optional): axis to compute values along. Default is the
first non-singleton axis.
Returns an array the same size as X. The result will sum to 1
along the specified axis.
"""
# make X at least 2d
y = np.atleast_2d(X)
# find axis
if axis is None:
axis = next(j[0] for j in enumerate(y.shape) if j[1] > 1)
# multiply y against the theta parameter,
y = y * float(theta)
# subtract the max for numerical stability
y = y - np.expand_dims(np.max(y, axis = axis), axis)
# exponentiate y
y = np.exp(y)
# take the sum along the specified axis
ax_sum = np.expand_dims(np.sum(y, axis = axis), axis)
# finally: divide elementwise
p = y / ax_sum
# flatten if X was 1D
if len(X.shape) == 1: p = p.flatten()
return p
def d_softmax(self, x):
J = - x[..., None] * x[:, None, :]
iy, ix = np.diag_indices_from(J[0])
J[:, iy, ix] = x * (1. - x)
return np.sum(J, axis = 1)
def xavier_trick(self,size):
if len(size) ==2:
c = np.sqrt(size[0]*size[1])*1e3
result = np.random.random(size)/c
else:
size = size[0]
c = np.sqrt(size)*1e3
result = np.random.random(size)/c
return result
def init(self):
self.W1 = self.xavier_trick(size = (self.INsize, self.HD1size))
self.W2 = self.xavier_trick(size = (self.HD1size, self.HD2size))
self.Wout = self.xavier_trick(size = (self.HD2size, self.OUTsize))
self.Wres = self.xavier_trick(size = (self.INsize, self.OUTsize))
self.B1 = self.xavier_trick(size = (self.HD1size,))
self.B2 = self.xavier_trick(size = (self.HD2size,))
self.B3 = self.xavier_trick(size = (self.OUTsize,))
def forward_pass(self, X):
l0 = X
l1 = self.tanh(np.dot(l0, self.W1) + self.B1)
l2 = self.ReLu(np.dot(l1, self.W2) + self.B2)
if self.isSoftMax:
l3 = self.softmax(np.dot(l2, self.Wout)+np.dot(l0, self.Wres) + self.B3,theta = 0.5, axis = 1)
else:
l3 = self.tanh(np.dot(l2, self.Wout)+np.dot(l0, self.Wres) + self.B3)
return l0, l1, l2, l3
def cross_entropy(self, p, y):
m = y.shape[0]
log_likelihood = -np.log(p[range(m),np.argmax(y, axis = 1)])
result = np.sum(log_likelihood)/m
return result
def delta_cross_entropy(self, grad, y):
m = y.shape[0]
grad[range(m),np.argmax(y, axis = 1)] -= 1
grad = grad/m
return grad
def backward_pass(self, l0, l1, l2, l3, y):
l3_delta = self.delta_cross_entropy(l3, y)
l2_error = l3_delta.dot(self.Wout.T)
l2_delta = l2_error*self.d_ReLu(l2)
l1_error = l2_delta.dot(self.W2.T)
l1_delta = l1_error*self.d_tanh(l1)
self.Wout -= self.learning_rate * l2.T.dot(l3_delta)
self.Wres -= self.learning_rate * l0.T.dot(l3_delta)
self.W2 -= self.learning_rate * l1.T.dot(l2_delta)
self.W1 -= self.learning_rate * l0.T.dot(l1_delta)
self.B3 -= self.learning_rate * np.sum(l3_delta, axis=0)
self.B2 -= self.learning_rate * np.sum(l2_delta, axis=0)
self.B1 -= self.learning_rate * np.sum(l1_delta, axis=0)
def fit(self, X, y, lr=0.1, isSoftMax=True):
self.isSoftMax = isSoftMax
self.learning_rate = lr
l0, l1, l2, l3 = self.forward_pass(X)
self.out_error = self.cross_entropy(l3, y)
self.backward_pass(l0, l1, l2, l3, y)
def predict(self, X, isSoftMax=True):
l0, l1, l2, l3 = self.forward_pass(X)
return l3
def reset(self):
self.init()
def __init__(self, input_size=2, layer1_size = 12, layer2_size = 12, output_size = 12):
self.INsize = input_size
self.HD1size = layer1_size
self.HD2size = layer2_size
self.OUTsize = output_size
self.init()def one_hot_encoding(y):
if np.min(y) > 0:
y = y-1
max_val = np.max(y) + 1
size = len(y)
result = np.zeros((size, max_val))
result[np.arange(size), y] = 1
return result.astype(int)
def normalize(x):
return (x-min(x))/(max(x)-min(x))def shuffle_split_data(X, y):
arr_rand = np.random.rand(X.shape[0])
split = arr_rand < np.percentile(arr_rand, 70)
X_train = X[split]
y_train = y[split]
X_test = X[~split]
y_test = y[~split]
return X_train, y_train, X_test, y_testdef accuracy(y_pred, y_true):
x_cl = [np.argmax(pred)+1 for pred in y_pred]
y_cl = [np.argmax(pred)+1 for pred in y_true]
res = 0
idx = 0
for xc, yc in zip(x_cl, y_cl):
res += 0 if xc == yc else 1
return ((len(x_cl) - res)/len(x_cl))*100def eval_model(model, X_train, y_train, X_test, y_test, lr = 0.1, batch_size = 10, isSoftMax = True):
epochs = 10
accuracy_by_epoch = []
error_by_epoch = []
batch_count = int(np.ceil(len(X_train)/batch_size))
for epoch in range(epochs):
for batch_number in range(batch_count):
batch_offset = batch_number*batch_size
batch_X = X_train[batch_offset:min(batch_offset+batch_size, X_train.shape[0]),:]
batch_y = y_train[batch_offset:min(batch_offset+batch_size, y_train.shape[0]),:]
#print("Batch #{} len {}".format(batch_number+1, len(batch_X)))
model.fit(batch_X, batch_y, lr = lr, isSoftMax = isSoftMax)
y_pred = model.predict(X_test)
acc = accuracy(y_pred, y_test)
accuracy_by_epoch.append(acc)
err = np.mean(np.abs(model.out_error))
error_by_epoch.append(err)
return error_by_epoch, accuracy_by_epochnp.random.seed(42)
data = np.genfromtxt("dataset/wine.data", delimiter=",")
y = one_hot_encoding(data[:,0].astype(int))
X = data[:,1:]
for r in range(X.shape[1]):
X[:,r] = normalize(X[:,r])
X_train, y_train, X_test, y_test = shuffle_split_data(X, y)
print("Train/test split: {}/{}".format(len(X_train), len(X_test)))
model = ResNet3(input_size=X_train.shape[1], layer1_size = 7, layer2_size = 9, output_size = y_train.shape[1])isSoftMax_vals = [True, False]
batch_size_vals = [10, 20, 30]
learning_rate_vals = [0.1, 0.01, 0.001]
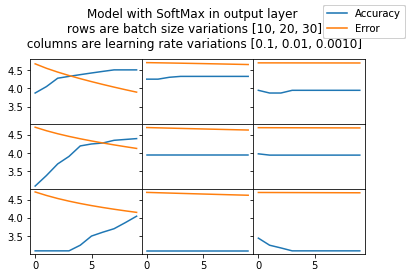
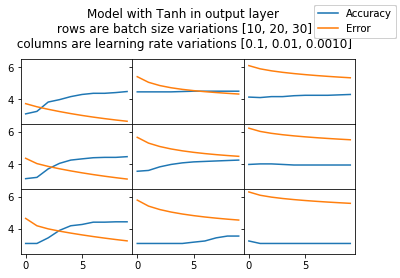
for isSoftMax in isSoftMax_vals:
f, axarr = plt.subplots(3, 3, sharex=True, sharey=True)
f.suptitle("Model with "+('SoftMax' if isSoftMax else 'Tanh') + " in output layer" +
"\n rows are batch size variations [10, 20, 30]" +
"\n columns are learning rate variations [0.1, 0.01, 0.0010]")
l1 = None
l2 = None
for batch_size in batch_size_vals:
for learning_rate in learning_rate_vals:
model.reset()
error_by_epoch, accuracy_by_epoch = eval_model(model, X_train, y_train, X_test, y_test, learning_rate,
batch_size, isSoftMax)
bsl = len(batch_size_vals)
lrl = len(learning_rate_vals)
plt_row, plt_col = batch_size_vals.index(batch_size), learning_rate_vals.index(learning_rate)
x = np.arange(0, 10, 1)
l1, l2 = axarr[plt_row, plt_col].plot(x, np.log(accuracy_by_epoch),
x, np.log([error*100 for error in error_by_epoch]))
f.legend((l1, l2), ('Accuracy', 'Error'), 'upper right')
f.subplots_adjust(top = 0.8, hspace=0, wspace=0)
for axrows in axarr:
for ax in axrows:
ax.label_outer()