A collection of concrete problems requiring an efficient algorithm. The proposed solutions are in Python to ease prototyping.
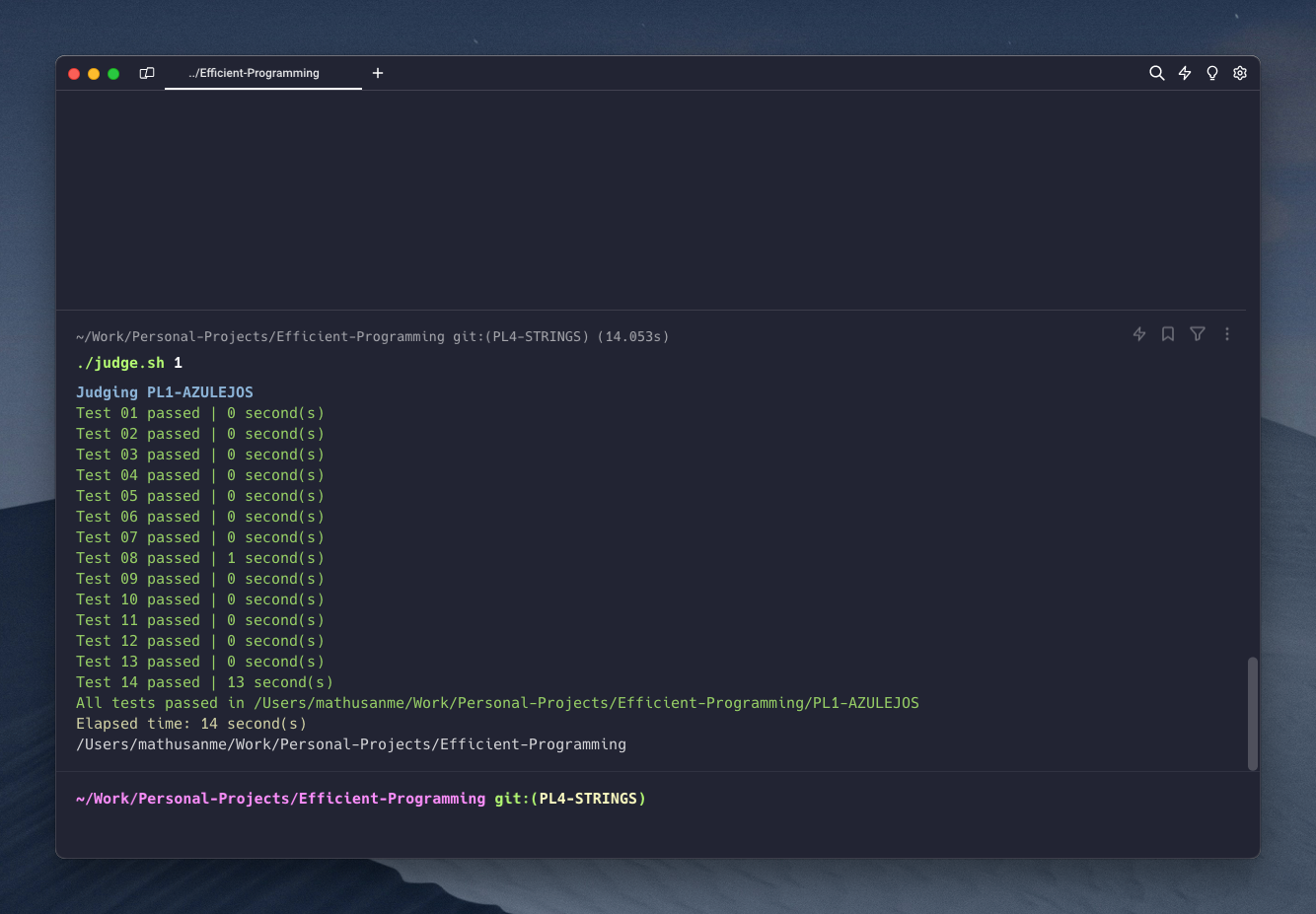
Two Portuguese ceramists team up to open an azulejos shop. They have a small shop window where they want to display some of their work in the most attractive and fair way possible: each will display the same number of azulejos. To make the most of the space available, they want to display two rows of tiles, one for each of the two artists, ensuring that all are clearly visible, including those in the back row. Each azulejo in the back row must be higher than the one in front of it. Another important point is to arrange the order of price: a customer attracted by one work will be able to admire others that they can also afford, only to give in to temptation and push open the shop door.
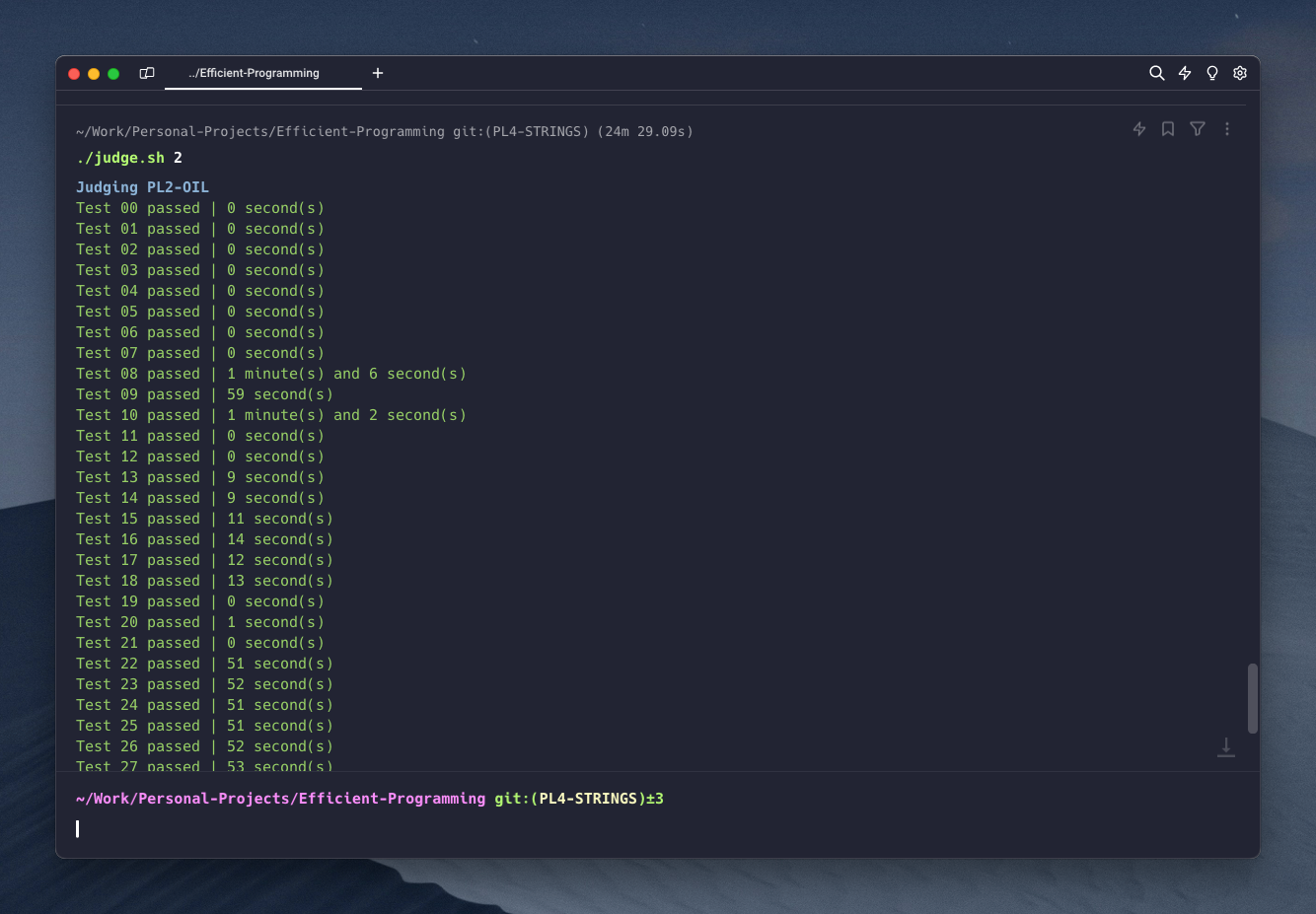
You work for an oil company and are responsible for optimising drilling. After decades of exploitation, drilling is becoming increasingly difficult: newly discovered deposits are often fragmented, which affects well productivity. You are being asked to consider the case of stratified deposits, i.e. deposits made up of several sub-deposits at different depths. You need to determine how to drill a single well to maximise its production. Drilling must be done in a single straight line, and it is assumed that the oil from each field crossed by the well be extracted (even if the intersection is at the end of the field). The capacity of each reservoir is equated to its width.
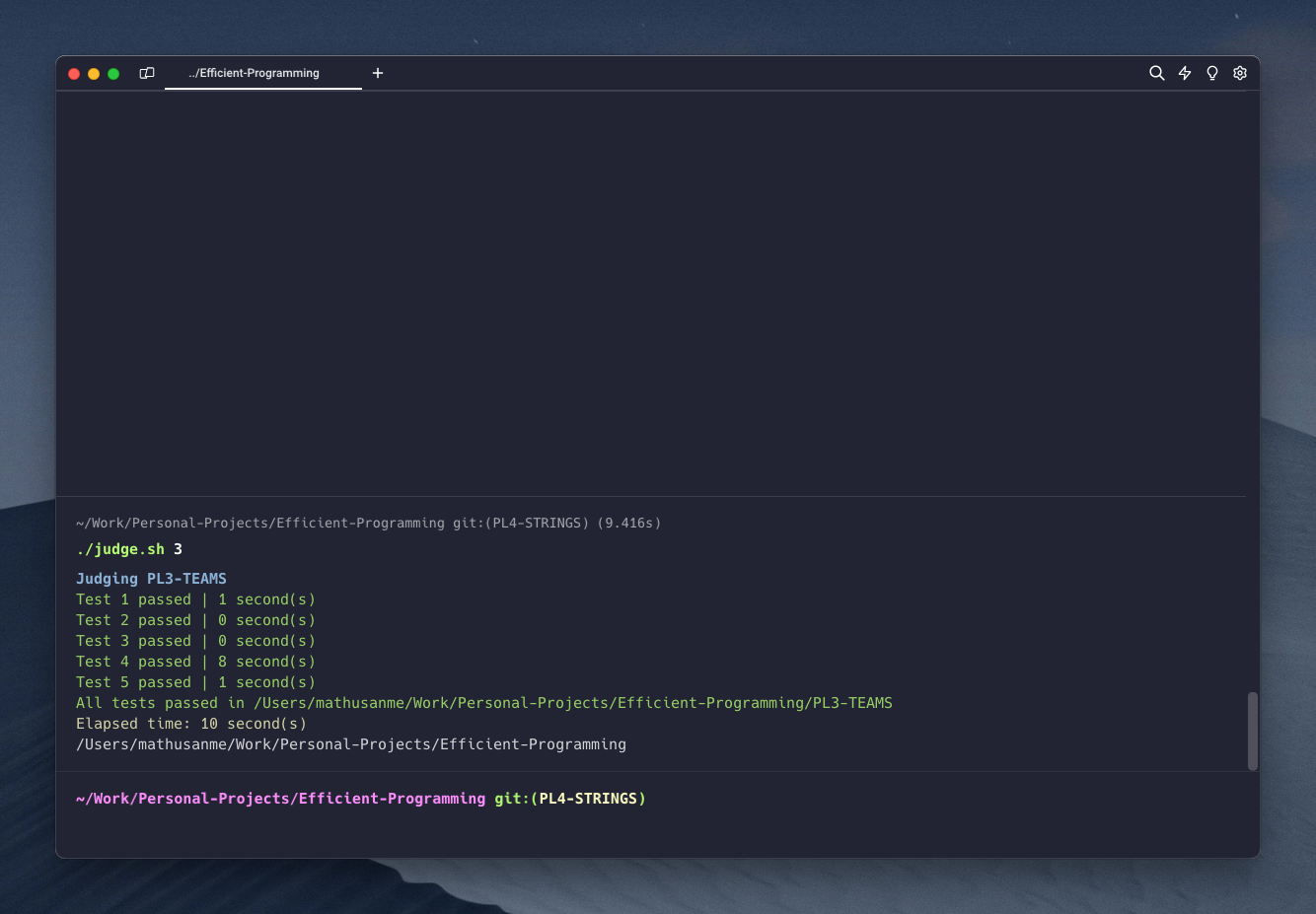
In this problem, we consider m players, and one referee, placed on certain vertices of a directed and weighted graph with n vertices (n > m) and r edges.
We aim to distribute the m players into p teams (with p ≤ m) in such a way that they can communicate as efficiently as possible among themselves, while adhering to strict rules: each day, every player from each team must send a message (different) to each of the other players in their team.
To ensure the rules are followed, all messages pass through the referee. To ensure their confidentiality, they are encrypted in a fairly basic manner: each player x has a personal key k_x known only to themself and the referee; to send a message to player y, x encodes their message with k_x, sends it to the referee who decodes it then re-encodes it with k_y and sends it to y.
The cost of a transmission is the sum of the weights of the arcs through which the message travels.
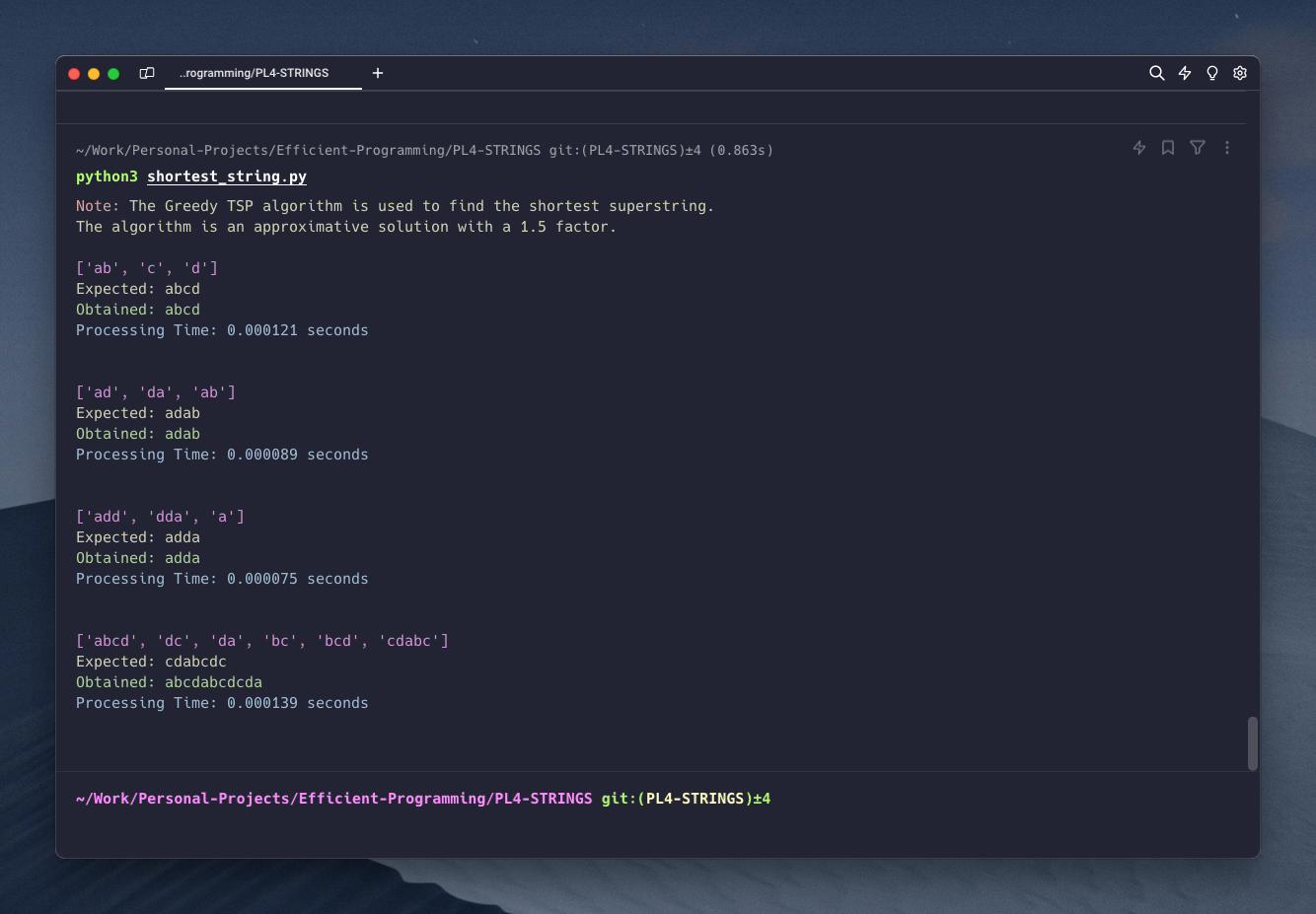
We are given n strings s1, s2, ... sn over an alphabet Σ. Find the shortest string over Σ that contains all the si (and its length).