marinavannucci / DGP-MCEM

R code for Monte Carlo EM algorithm of derivative Gaussian process model - Yu et al. (2022, Biometrics)

DGP-MCEM

This repository contains relevant R code for implementing the Monte Carlo Expectation Maximization (MCEM) algorithm of the Derivative Gaussian Processes model. In addition to estimating a nonparametric regression function, the model and the algorithm (DGP-MCEM) infer the locations of stationary points of the function by providing the full posterior distribution of the stationary points. The approach has been applied to the estimation of event-related potentials (ERP) derived from electroencephalography (EEG) signals. For more details about DGP-MCEM model and algorithm, please read the paper Yu et al. (2020). Bayesian Inference for Stationary Points in Gaussian Process Regression Models for Event-Related Potentials Analysis

Demo and Usage

Required packages and R version

The required R packages include Matrix, matrixcalc, Rsolnp, emulator, R.utils. The package parallel and doParallel are used for simple multi-core computing. The latest R version is recommended, but any version >= 3.6 should work.

Simulated Data and ERP data

All 100 simulated data sets for analysis in the paper are stored in ./data/sim_data.Rdata. The simulated data are generated using the script creat_sim_data.R in the folder ./data-raw. The ERP data are stored in the 4 Rdata formatin the folder ./data: subj_y.RData, y_bias.RData, subj_y_old.RData, y_bias_old_11_bias_only.RData.

Starts with a demo

The R script demo.R provide an example to illustrate how the algorithm is implemented with a simulated data set. The data set is the first simulated data set stored in ./data/sim_data.Rdata. The main functions of MCEM are in the script mcem_fcns.R in the ./R folder. In particular, mcem_dgp() function implements MCEM with single-DGP and mcem_dgp_multi() function implements MCEM with multiple-DGP. The functions return a list including samples of stationary points sample_t, samples of $\sigma$, sample_sig and the values of hyperparameters in the covariance function of every iteration, saved as thetas.

Full simulation study

The entire simulation study in the reference paper can be reproduced by running the script simulation_main_mcem.R, including comparing single-DGP, multiple-GDP and ordinary Gaussian process regression (GPR).

The simulation results are stored in sim_result_algo.RData for running algorithms, and sim_pred_gp_lst.RData, sim_pred_dgp_oracle_lst.RData, sim_pred_dgp_single_lst.RData, sim_pred_dgp_multiple_lst.RData for information about samples of $f$. To save time running, one can load these data for further analysis. A matern kernel analog of simulation study is performed in simulation_main_matern_mcem.R.

Full Data Analysis

The full ERP data analysis is performed in data_analysis_subject_sig_mcem.R. The script data_analysis_subject_sig_mcem.R performs the multiple-DGP analog of analysis.

Figures in the paper

To reproduce every figure shown in the paper, run the script figures_paper_mcem.R.

Supplementary materials

Analysis in the supplementary materials can be found in other R scripts that are not mentioned.

Basic Results from demo.R

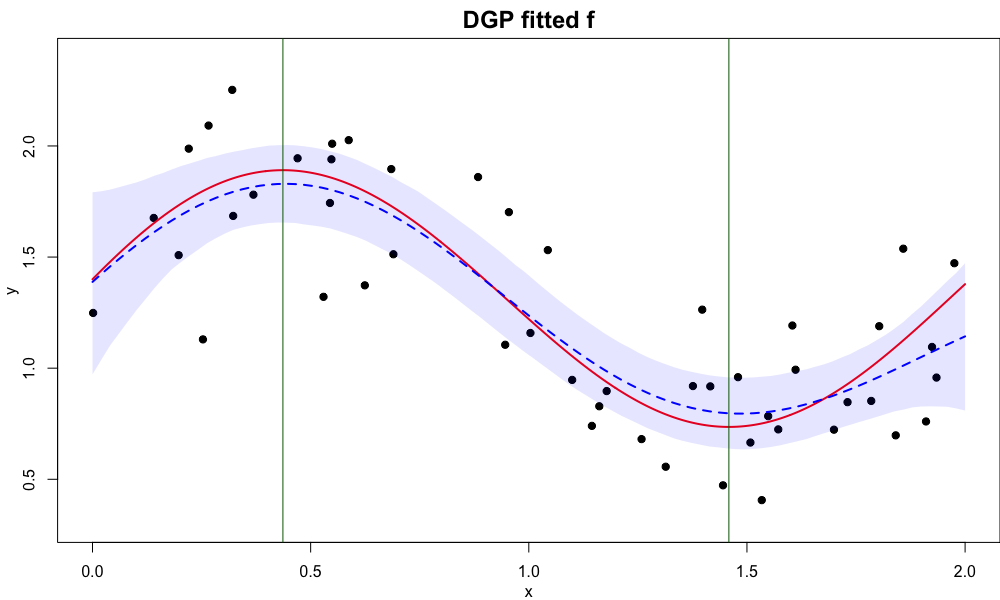
The data and fitted result is shown in the image below.

The red curve is the true regression function, and blue dash curve is the posterior mean curve after drawing 100 sample paths of $f$. The light blue shaded area indicates 95% credible band for $f$. Two green vertical lines indicate the location of stationary points.

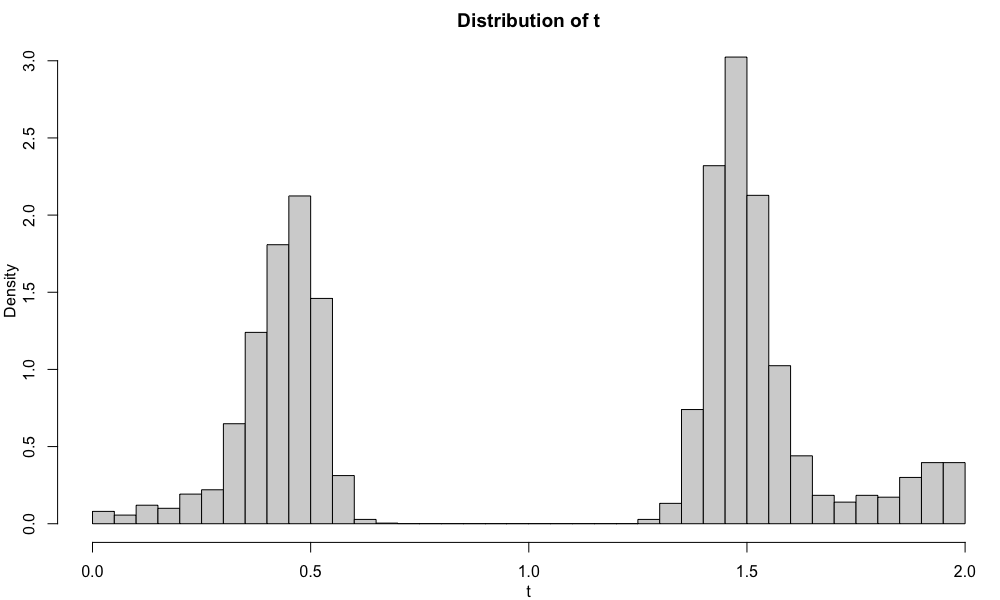
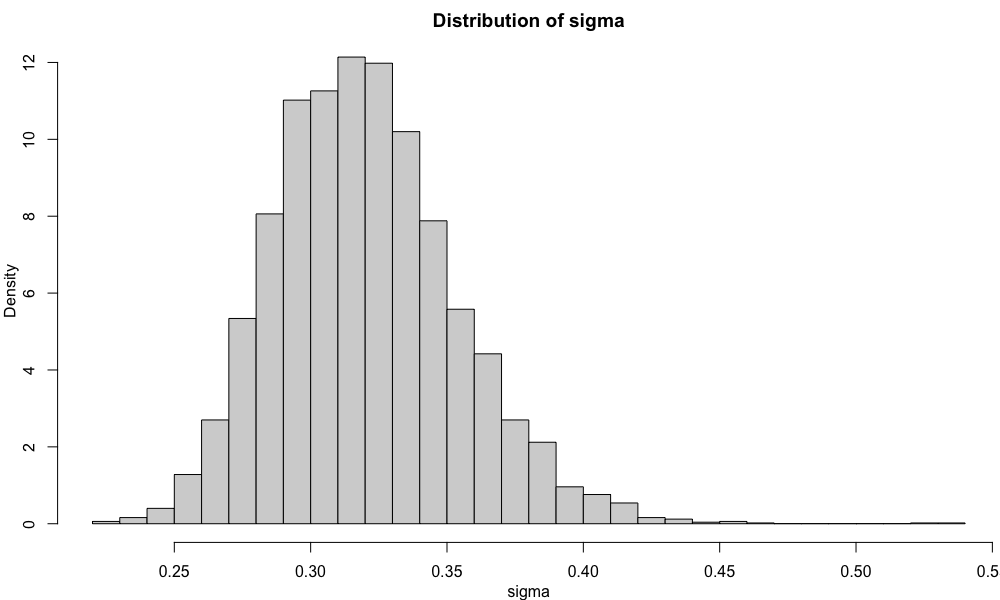
The distributions of $t$ and $\sigma$ are generated directly from the Monte Carlo step in the MCEM algorithm. These distributions are obtained without the need of sampling paths of $f$.