Push Fight is solved completely! With the help of these volunteers I was able to calculate the best move for any valid position of the game.
Push Fight is an abstract board game for two players designed by Brett Picotte. A summary of the rules is provided further down. For more information about the game, or if you want to buy a physical copy to play with, visit https://pushfightgame.com/
The project has two main results: a data file that classifies all possible positions, and a website that allows any position to be evaluated. As a bonus, the website also allows playing against an AI that can play either perfectly (and thus will never lose) or with a variable playing strength.
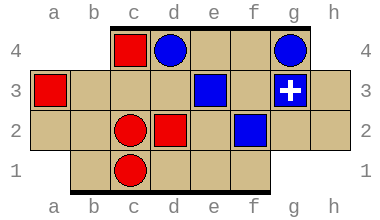
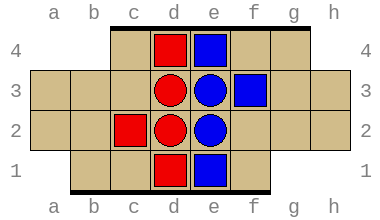
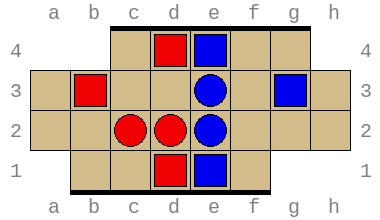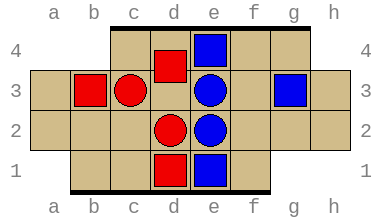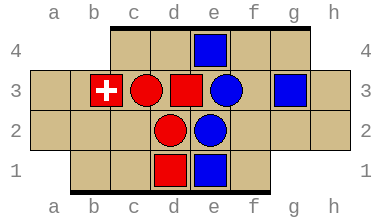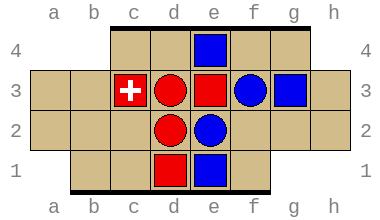
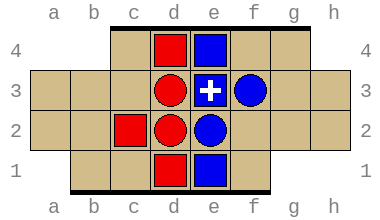
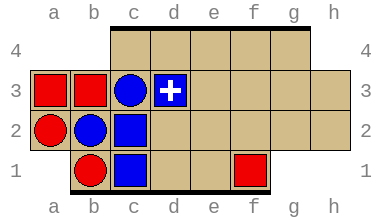
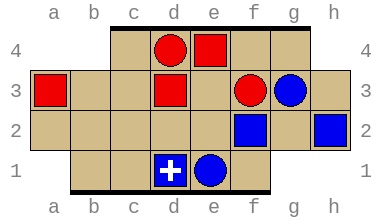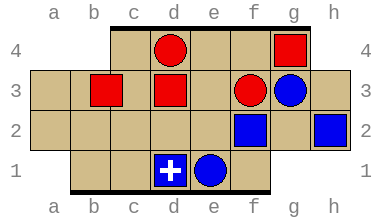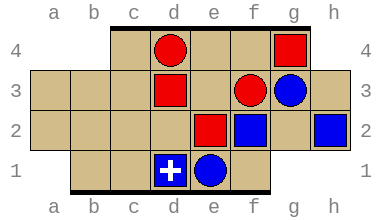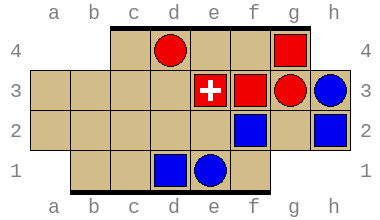
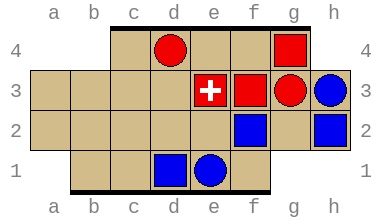
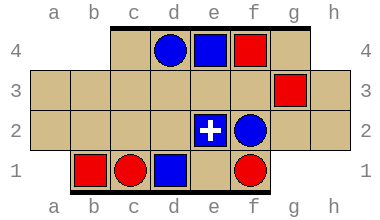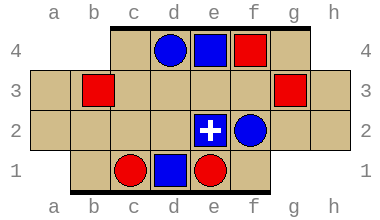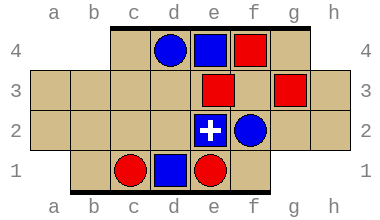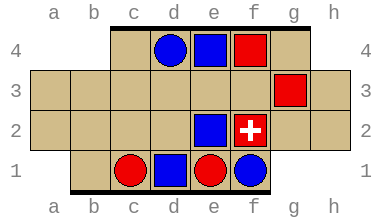
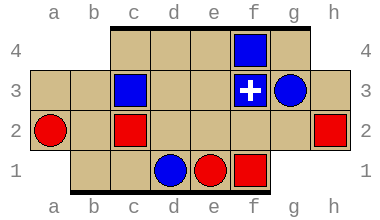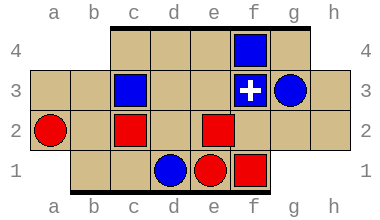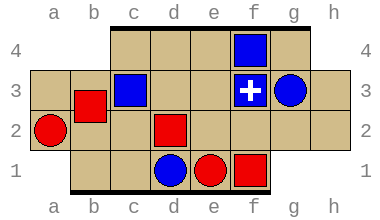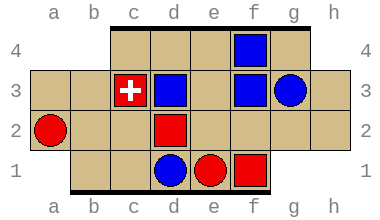
Combined, these allow exploring arbitrary positions and discovering wins and losses requiring superhuman insight. For example, the position below (permutation index 316452211876) is won by Red in no less than 49 turns (or 97 total turns) with optimal play:
The main goal of the project was to calculate, for every valid position, whether it was winning, losing or tied, and if so, in how many moves. This also allows optimal moves to be recovered (by evaluating the status of successors).
The data files are available here: https://styx.verver.ch/~maks/pushfight/
There are two files of interest:
- merged.bin is a 401 GB file that contains one byte per position, indicating the status of that position (how positions correspond with byte offsets is described below.)
- minimized.bin is an 86 GB file that contains the same data, excluding unreachable positions and eliminating positions that are equivalent by rotation.
Each of these files can be generated from the other. minify-merged converts merged.bin to minimized.bin, and expand-minimized converts minimized.bin back to merged.bin, but the former transformation is much faster than the latter, because expanding the minimized file requires recalculating the value of all unreachable positions.
I verified the internal consistency of minimized.bin using verify-minimized, which took several weeks. This proves the absence of data errors (e.g. due to corruption on disk), but it only proves correctness under the assumption that the game logic is correctly implemented. I believe this is true but I haven't proven it formally.
I created a little web app to analyze arbitrary positions, which allows people to experiment with the game without downloading any data files.
The Push Fight Analyzer app is available here: https://styx.verver.ch/pushfight/ or here: https://pushfight.verver.ch/
The main features are:
- Setup: configure an arbitrary starting position, or import from a known permutation index (described below) or permutation string.
- AI tab: let AI control one of the players to practice. The AI's playing strength is variable. At maximum strength, the AI plays perfectly, which means it can never lose and will exploit even the smallest mistake on the player's part!
- Move history tab: shows the moves played in the game so far, optionally annotated with the valuation at the beginning of the turn. This makes it easy to see when a player makes a mistake. It's also fun to analyze past matches this way!
- Analysis tab: shows all possible successor states, grouped by outcome. This allows you e.g. to see which moves are optimal in a particular position.
Tip: you can copy/paste the URL of a game in progress to store the game state including the move history. This allows you to store a game for later (e.g. by bookmarking it) or to share it with others.
The website can also be run locally, as a standalone app (see pushfight-standalone-server.cc). I'll make a binary release of this later.
The Git repository contains most of the code used to solve the game. This could be used to reproduce or validate the output files. An overview:
- README.md (this file) contains a description of the game, some interesting properties, and information about the process of solving the game completely.
- The server/ directory contains the server implementation that was used to solve several phases as part of a distributed computing project (see this topic on the Tweakers.net forum). This server is no longer online.
- The metadata/ directory contains data from the intermediate files, such as checksums and position counts.
- The results/ directory contains some interesting facts about the games discovered by solving the game, such as counts of how many positions are won-in-1 etc. (these can be inferred from merged-bytecounts.txt and minimized-bytecounts.txt, and sample game ids of each (merged-samples.txt and (minimized-samples.txt).
- The html/ directory contains the Push Fight Analyzer web app implementation. Contrary to what the directory name suggests, this not plain html, but written in React with NPM and Webpack. See the README for details.
Throughout the project I made several interesting observations. I'll provide a summary below for people who like that sort of thing.
-
The project started when I realized it's possible to map board positions to a compact range of integers, creating a bijection between positions and numbers between 0 and N, where N is reasonably small. Without this realization, the project would have been infeasible. Storing data in a conventional key-value store would be a nonstarter: even using just 50 bytes per key-value pair would require about 20 terabytes of storage, which I don't have.
Throughout the project I made extensive use of this bijection, which makes it unnecessary to store keys explicitly and allows storing just an array of values where the indices correspond with positions. So I ended up using bitmaps (1 bit per position, or about 50 GB for the entire game) and ternary data files (with 3 possible values, tie, loss or win, or 1.6 bits per position, or 80 GB for the entire game), and even the final output is a flat array with 1 byte per position (though I only need 7 bits).
-
It's possible to eliminate rotations and unreachable positions without giving up the compact index! I knew from the start that there was some redunant work being done because some positions are either unreachable (and therefore we don't care about their valuation) or they are equivalent to a rotated position (and we only need to store one of them), but I didn't try to remove this redundancy because I thought it would destroy the bijection between game positions and permutation indexes. Later I found a bijection that excludes those redundant positions; these are called minimized indexes (described down below) and reduce the total number of values from around 401 billion to around 86 billion. If I had discovered this sooner I might have used minimized indices for everything. It would have reduced the size of intermediate files considerably, though on the other hand minimized indices are more expensive to compute, so this could have come at the cost of increased CPU usage.
-
We can calculate the predecessors of a position almost as easily as the successors (and positions have roughly the same number of successors as predecessors)! I hadn't initially realized this was practical, but when I did, it led to the invention of the loss-backpropagating solvers (described further down), which ran much faster than the equivalent forward-searching solver (which works for both wins and losses). Without this discovery, solving the game would have been possible but would have used much more CPU time.
-
You can calculate two phases at once! Initially, I conceived of the solver as a fixed point iterator: you make one pass over all undecided positions, and classify them based on the valuation of their successors. Then you repeat until you've reached a fixed point (i.e., no new positions are classified). It soon became clear that this algorithm effectively alternates between discovering losses and discovering wins. After all, you can only discover a win if some of the successors are classified as losses, and discover a loss if all of the successors are classified as wins. So in each run of the algorithm (which I call a phase) you discover new losses, or new wins, but not both.
This was useful during the distributed computation part of the project. Initially, I had participants download an entire input file, and then run the fixed-point iteration algorithm or to backpropagation algorithm to discover new losses or wins. Each participant would only compute the results for a subarray of the file (a so-called chunk of work). Between phases, I had to integrate the results and send a new data file to all participants. But I noticed that loss backpropagation doesn't depend on the previous phase's output at all, so it's possible to combine the two phases, so that each participant calculates both wins and losses in a single pass. That's why later phases were solved two-at-a-time. This was beneficial to me because every phase required some manual work on my part, so doing two phases at once effectively halved the administrative burden for me.
The solve2 and solve3 solvers both solve two phases at a time.
Push Fight is a game for two players on a board with 4 rows and 8 columns, with some squares missing. Rows are labeled 1 through 4 (from bottom to top) and columns are labeled a through h (from left to right), as in Chess. See below:
Each player controls five pieces: two round pieces and three square ones. The game starts with the first player (in my version, red) placing their pieces anywhere on the left half of the board (columns a through d), then the second player placing their pieces on the right half of the board (columns e through h), and then the red player plays the first turn.
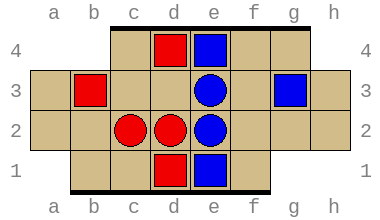
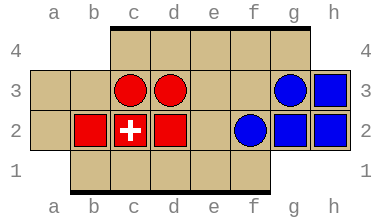
Below are two possible starting positions:
During a turn, a player can make 0, 1 or 2 moves and then must end with exactly 1 push. If a player cannot push, he or she loses the game immediately. A move consists of taking a piece of the player's color (either a square or a round one) and moving it to any free square that is reachable through a sequence of horizontal and vertical moves. Finally, a push involves taking a square piece of the player's color and moving it exactly 1 space up, down, left or right, pushing pieces that are in the way in the same direction. At least 1 other piece must be pushed, though it doesn't matter what color or shape the pushed pieces are.
Below is an example of the first turn for the red player, starting from the second starting positon above. (The image below is an animated GIF. You may have to click the play button to view it.)
Pieces cannot be pushed past the railing at the top and bottom of the board. However, pieces can be pushed off the board on the left and right side (and off the top or bottom of squares like b3 and g2). The first player who manages to push an opponent's piece off the board, wins.
There is one final rule. After a player has performed their push move, a special piece called an anchor is placed on the pushing piece. The opponent may not push that piece during the next turn. This prevents obvious stalemates with players pushing the same row of pieces back and forth, and also adds some tactical opportunities to the game.
For convenience, let's define human-readable textual representation for positions and moves. It's fairly easy to encode the board in text:
abcdefgh
4 .OX.. 4
3 ...oxY.. 3
2 ..Oox... 2
1 ..OX. 1
abcdefgh
In this notation, o is a red circle (mover), O is a red square (pusher),
x is a blue circle (mover), X is a blue square (pusher), and Y is a blue
square with an anchor on top. Some tools also use P for a red square with
an anchor, but as will be explained below, we can usually assume without loss
of generality that the anchor is on a blue square.
If we want a more compact representation, we can remove the board coordinates:
.OX..
...oxY..
..Oox...
..OX.
and put all characters on a single line:
.OX.....oxY....Oox.....OX.
Now, we've reduced the board to a single 26-character string. This is what I call a permutation string, and this format is accepted by most tools, including the web app.
For moves, we can use a chess-like notation. For example, c2-d2 represents a
push to the right, and d1-a2,d3-c3,c2-d2 represents two moves followed by a
final push. Note that the push is necessarily the last move in the sequence,
and it's also clear from the board, since moves always end in an empty square
while pushes must move a piece to an occupied square.
Push Fight is an interesting game because of how constrained it is: the board consists of only 26 squares, with 10 total pieces (5 for each player). Although it's possible to push a piece off the board, this immediately ends the game, so in any intermediate position all 10 pieces will be present.
If we ignore the anchor for a moment, that means all positions can be
represented as permutations of a 26-character string that consists of
16 . (empty spaces), 2 os, 3 Os, 2 xs, and 3 Xs. The total number
of permutations is:
where x! represents the factorial of x. However, this doesn't account for the placing of the anchor, which can be on any of the 6 square pieces or not in play at all. Seemingly, this would multiply the number of positions by 7. However, if we're willing to treat the first turn specially and we only want to be able to represent positions from turn 2 and on, we can assume the anchor is in place.
Additionally, we can assume that the anchor is always on one of the second
player's squares, since the game board is symmetric, so we can always swap the
colors of the pieces. So without loss of generality, we will assume it's the
red player's turn to move, and the anchor is on one of the blue player's squares.
This means we will replace one of the Xs with an Y, and all positions are
now some permutation of the string:
................ooOOOxxXXY
The total number of such permutations is:
This means every board position has an associated permutation index between 0 and 401,567,166,000 (exclusive). It turns out that, with some precomputation, it's possible to efficiently convert between board positions and permutation indices. Efficiently here means O(N) where N is the number of squares on the board. See the logic in perms.h and perms.cc for details.
Does every permutation represent a reachable position, in the sense that it can be reached from a starting position by some sequence of valid moves (no matter how improbable)? No, in fact, there are some permutations that are provably unreachable, due to the placement of the anchor.
Recall that the anchor is placed on the opponent's piece that made the last push move. That implies there must be a preceding position where this piece was in a different place and pushed in a particular direction, moving at least on other piece, and leaving an empty square behind. In the resulting position, there must be some direction that has a piece next to the anchor, and an empty piece on the opposite side. For example: a piece above the anchor and an empty square below the anchor implies the anchored piece could have pushed up from the square below.
If there is no direction such that there is a piece on one side and an empty square on the other side, then the position is clearly unreachable. An example is given below:
In the above position, the anchored piece on square e3 could not have come from anywhere, so while this is a valid permutation, it is not reachable through normal play.
It follows from the above that the anchor can never be on some squares (the eight corner squares: a2, a3, b1, c4, f1, g4, h2, and h3).
We can calculate (see calc-minimal-permutations.py) that out of 401,567,166,000 total permutations, 172,416,263,040 (42.94%) are reachable and 229,150,902,960 (57.06%) are unreachable.
This was also confirmed by a brute-force search (see count-unreachable.cc and the output in count-unreachable-output.txt).
There are also positions that cannot be reached because all of their predecessors are unreachable. An example is below:
However, these positions can technically still be reached in 1 move from an appropriate starting position.
There are similar positions that may be truly unreachable because the pieces are not on the right side of the board for a valid starting position, but I did not bother to exclude those.
The board has 180 degrees rotational symmetry. For each permutation, we can calculate a twin by rotating the pieces around the center. These twins are always distinct (i.e., there are no rotationally symmetric positions) as can be seen by the presence of the unique anchor piece, which is always at the top half of the board in one rotation and at the bottom half in the other (similar arguments can be made about the red pushers).
Normalizing for this reduces the total number of reachable permutations to 86,208,131,520 permutations up to rotation.
Just like it's possible to map permutations to compact indices from 0 to ~401 billion, it's possible to map reachable permutations to minimized indexes between 0 and ~86 billion (ignoring rotation).
For details, see the functions MinIndexOf() and PermAtMinIndex() in
perms.h and perms.cc.
To solve the game, we need, at a minimum, to decide for each position if it's winning, losing, or tying for the next player. Ideally, we would also like to record either a winning move or the number of turns left until a win/loss occurs, so we can enumerate the different options.
Note that a position is tying if neither player can force a win. In that case, the game would go indefinitely (assuming optimal play from both sides). It's not clear if tying positions exist, but it seems likely.
To compute results we need to consider the successors of a position: all
positions that are reachable in exactly 1 turn. In Push Fight, a turn consists
of up to two moves and one push, so the number of successors can be quite large
(
We can think of the game as a graph, with nodes representing board positions and (directed) edges as possible moves. In other words, the edge (p, q) is in the graph is q is a successor of p, and q is an intermediate position. Positions reached after pushing a piece off the board are not included in the graph.
The general algorithm for classifying nodes in the graph works as follows.
Rule 1: for a position p, if there is a way to win at the current turn, we can mark the node as winning.
Rule 2a: otherwise, if there is any successor q that is marked losing, then we can mark p as winning.
Rule 2b: otherwise, if all successors are marked winning, then we can mark p as losing.
This leads to the following algorithm to solve the game:
- Phase 0: loop over all positions, and apply rule 1. This marks some positions as winning, while leaving the rest undetermined.
- Phase 1: loop over all positions that are yet undetermind, and apply rules 2a and 2b. This marks some undetermined positions as winning or losing, leaving the rest undetermined.
- Phase 2..N: repeat the logic from phase 1 until no more changes occur.
The logic for phases 2 and up is implemented in solve-rN.cc.
This is a fixed-point iteration algorithm where we classify more and more positions until we cannot find any more positions that can be classified by rules 2a and 2b. At this point, we can stop and assume that all remaining indetermined positions are actually ties.
We don't know in advance how many phases are necessary to compute the fixed point.
The phases have some interesting properties. In phase 0 we only find winning positions. The means in phase 1, we can only identify newly-losing positions because to identify a non-immediate winning position requires a losing successor (rule 2a) which we haven't found yet. In phase 2, we can only find newly-winning positions because identifying a losing position requires all successors are winning for the opponent (rule 2b) and the previous phase didn't find any.
And so on: the phases alternate between finding only losing and winning positions, with even phases finding winners and odd phases finding losers.
To allow the work of calculating a phase to be distributied, I split the input into 7429 chunks of 5,4054,000 permutations each. This allows solvers running on multiple computers to calculate the results for different input chunks independently. To calculate the combined output file, it's necessary to collect the generated output files and concatenate them.
The game Push Fight has the interesting property that it isn't much more difficult to generate the predecessors of a position than the successors. (A predecessor of a position q is a position p such that p has a valid move that leads to q.)
This makes it possible to calculate the winning positions in a different way. Instead of looping over the undecided positions, searching for successors where the opponent loses, we can loop over all the positions that were marked losing in the previous phase, and mark all their predecessors as winning.
This approach is advantageous for two reasons. One is that after the first few phases, the number of newly-losing positions is much smaller than the number of undecided positions (by a factor of 20 or so), while the number of predecessors is roughly the same as the number of successors. That means backpropagating losses can be up to 20 times faster.
Does this mean that the calculation of even phases (where we find wins) is much faster than odd phases? No, it turns out the approach implemented by solve-rN is perfectly suitable for odd phases. The reason is that it's much easier to prove that a position is not losing (finding a single tied successor is sufficient) than to prove that a position is not winning (which requires enumerating all the successors to show than none of them are lost by the opponent). So although the solve-rN solver has to process more positions, it can process them more quickly (in odd phases only!)
The loss backpropagation logic is implemented in two solvers: backpropagate-losses.cc and backpropgate2.cc. They differ in the output file format. backpropagate-losses creates a single 50 GB bitmap with new wins marked as 1. This bitmap is shared between input chunks, so it never grows. backpropagate2 on the other hand writes a list of permutation indices that were newly discovered to be winning. The downside of the second approach is that different input chunks can have some duplicates in their output (a newly winning position can be a predecessor of multiple losing positions that occur in different input chunks).
The bitmap output file from backpropagate-losses deduplicates by overwriting the same bit in the bitmap. However, this deduplication only happens on a single machine, so the more different machines are participating in the computation, the less effective the bitmap approach is at eliminating duplicates. Therefore, the backpropagate-losses tool scales less well with multiple participants.
Finally, it's possible to combine these ideas, using a forward search from each undecided position to find new losses, and then using a backward search from each new loss to find new wins. The advantage of this approach is that only the even-number input files ever need to be generated.
This method is implemented in solve2, which outputs two lists for each input chunk: one with the newly discovered losses (corresponding with the results of solve-rN) and one with the newly discovered wins (corresponding with the results of backpropagate2). Note that that new losses will be discovered in the range corresponding with the input chunk, while new wins can appear anywhere, and so the second lists of all chunk output files can still contain duplicates.
The combined strategy is most effective in later phases, when the number of new wins and losses becomes relatively small.
Finally, it's also possible to backpropagate newly-discovered wins. To do that we would look at all the predecessors of the winning position, and consider their successors: if all successors are won by the opponent, then we can mark the predecessor as losing.
Note that this is less efficient than loss backpropagation, since we need to consider all successors of a predecessor, rather than just the predecessor itself. If we assume a position has about 2,000 predecessors and successors on avarage, that means we'll have to check ~2,000 positions when backpropagating losses, and ~4,000,000 positions when backpropagating wins. Obviously the latter is much slower.
We could speed this up by maintaining some auxiliary data per indeterminate position which prevents the need to re-evaluate all successors, such as the number of indeterminate successors (which is decremented whenever we identify a new win), or a reference to one inderminate successor (which we'd update whenever that successor is marked as a win). However, storing this extra information would take a lot of extra disk space (e.g., two bytes per permutation would require another 800 GB total), so I decided against it for now.
At some point, the number of newly-discovered positions in a phase could become so small that backpropagating wins becomes the more effective strategy.
Phase 0 classifies each possible value as winning or undetermined. Therefore we can suffice with 1 bit per position, creating an output file of 401,567,166,000 bits, or 50.2 GB.
Phase 1..N need to produce a ternary value (winning, losing or undetermined). We can encode 5 ternary values in a byte to obtain an efficient of 1.6 bits per value, creating an output file of 80.3 GB.
Note that phase 1 is a little special in that it consumes the binary output from phase 0, while phases 2 and on instead use a ternary input file that they also use as an output file.
The above data structures, once computed, can be used to classify an arbitrary position (winning, losing or tied), though only after turn 1, when the anchor is present. However, this information by itself isn't enough to come up with a winning strategy.
For a losing position, it doesn't matter which moves we choose: by definition, any successor is winning for the opponent and therefore losing for us.
For a tied position, we can simply choose any moves that lead to a successor that is also tied: by definition, the opponent cannot win from that position (and also by definition, a tied position cannot have successors that are losing for the oppponent, or it would have been classified as winning).
For a winning position, we must choose moves that lead to a successor that is marked losing for the opponent (and thus winning for us). But we cannot just pick arbitrarily! If we do, and we're unlucky, we would end up in an infinite loop.
So to recover the correct winning strategy, we need to keep a little more information: the number of turns it takes to win/lose. That way, we can pick the successor that leads to a win in the fewest possible moves.
More formally, if a position is losing because it has no successors, we mark it as losing in 0 turns; otherwise, it is losing in (K + 1) turns where K is the maximum value of a successor that is winning in K turns. Similarly, a position with an immediate winning push is winning in 1 turn, and otherwise, the position is winning in (K + 1) turns where K is the minimum value of a successor that is losing in K turns.
This means we need a bit of additional data to store per position: the number of turns it takes to achieve the outcome. How much space is needed for this depends on the length of the longest path to a forced win, which is equal to the number of times we need to execute the fixed point algorithm.
Note that we can save 1 bit by observing that in the above, losing positions are always losing in an even number of turns (0, 2, 4, etc.) while winning positions are always winning in odd number of turns (1, 2, 5, etc.) This makes sense because there are only two ways for you to win: either you push an opponent's piece off the board, or the opponent is unable to push on their turn; either way, you made the last move, which means that if you are in a winning position, you will always play one more turn than your opponent.
So how can we recover the number of turns remaining from the ternary output files? Simple: positions won in 1 turn are identified in phase 0. The positions lost in 2 turns are first identified in phase 1. The positions won in 3 turns are identified in phase 2. And so on. So we simply need to find, for each position, in which phase it was first classified. This gives the number of turns left to play.
We can summarize this in a new data structure, but to do so efficiently, we need to know exactly how many phases there are, since the number of phases corresponds with the maximum number of turns leading to a win.
- Phase -1: solve-lost.cc
- Phase 0: solve-r0.cc
- Phase 1: solve-r1.cc
- Phase 2: backpropagate-losses.cc
- Phase 3—8: solve-rN.cc (odd numbered phases) and backpropagate2.cc (even numbered phases)
- Phase 10—58: solve2.cc (solves two consecutive phases at a time)
- Phase 60—98: solve3.cc (solves two consecutive phases at a time)
The table below shows how many positions were classified during each phase of the computation.
| Phase | Undetermined | Losses | Wins | New Losses | New Wins |
|---|---|---|---|---|---|
| -1 | 401,567,165,352 | 648 | 0 | 648 | 0 |
| 0 | 60,779,916,660 | 648 | 340,787,248,692 | 0 | 340,787,248,692 |
| 1 | 54,546,852,886 | 6,233,064,422 | 340,787,248,692 | 6,233,063,774 | 0 |
| 2 | 37,780,557,416 | 6,233,064,422 | 357,553,544,162 | 0 | 16,766,295,470 |
| 3 | 34,837,304,642 | 9,176,317,196 | 357,553,544,162 | 2,943,252,774 | 0 |
| 4 | 29,666,435,732 | 9,176,317,196 | 362,724,413,072 | 0 | 5,170,868,910 |
| 5 | 27,888,385,386 | 10,954,367,542 | 362,724,413,072 | 1,778,050,346 | 0 |
| 6 | 25,632,393,438 | 10,954,367,542 | 364,980,405,020 | 0 | 2,255,991,948 |
| 7 | 24,512,388,568 | 12,074,372,412 | 364,980,405,020 | 1,120,004,905 | 0 |
| 8 | 23,255,798,284 | 12,074,372,412 | 366,236,995,304 | 0 | 1,256,590,284 |
| 10 | 21,713,847,582 | 12,816,540,474 | 367,036,777,944 | 742,168,062 | 799,782,640 |
| 12 | 20,639,324,942 | 13,339,114,688 | 367,588,726,370 | 522,574,214 | 551,948,426 |
| 14 | 19,793,983,428 | 13,759,271,414 | 368,013,911,158 | 420,156,726 | 425,184,788 |
| 16 | 19,039,824,268 | 14,149,521,144 | 368,377,820,588 | 390,249,730 | 363,909,430 |
| 18 | 18,434,317,480 | 14,461,603,082 | 368,671,245,438 | 312,081,938 | 293,424,850 |
| 20 | 17,998,132,092 | 14,685,061,622 | 368,883,972,286 | 223,458,540 | 212,726,848 |
| 22 | 17,699,545,846 | 14,831,345,732 | 369,036,274,422 | 146,284,110 | 152,302,136 |
| 24 | 17,474,516,838 | 14,942,516,496 | 369,150,132,666 | 111,170,764 | 113,858,244 |
| 26 | 17,310,522,604 | 15,022,875,636 | 369,233,767,760 | 80,359,140 | 83,635,094 |
| 28 | 17,185,509,474 | 15,083,910,952 | 369,297,745,574 | 61,035,316 | 63,977,814 |
| 30 | 17,081,557,558 | 15,137,192,422 | 369,348,416,020 | 53,281,470 | 50,670,446 |
| 32 | 16,991,731,644 | 15,180,817,806 | 369,394,616,550 | 43,625,384 | 46,200,530 |
| 34 | 16,916,463,452 | 15,217,757,052 | 369,432,945,496 | 36,939,246 | 38,328,946 |
| 36 | 16,851,338,398 | 15,253,531,202 | 369,462,296,400 | 35,774,150 | 29,350,904 |
| 38 | 16,802,533,774 | 15,277,462,920 | 369,487,169,306 | 23,931,718 | 24,872,906 |
| 40 | 16,750,077,176 | 15,301,255,914 | 369,515,832,910 | 23,792,994 | 28,663,604 |
| 42 | 16,701,027,140 | 15,327,096,436 | 369,539,042,424 | 25,840,522 | 23,209,514 |
| 44 | 16,663,048,812 | 15,345,782,968 | 369,558,334,220 | 18,686,532 | 19,291,796 |
| 46 | 16,625,288,850 | 15,364,843,234 | 369,577,033,916 | 19,060,266 | 18,699,696 |
| 48 | 16,586,488,724 | 15,385,369,328 | 369,595,307,948 | 20,526,094 | 18,274,032 |
| 50 | 16,546,438,186 | 15,408,160,720 | 369,612,567,094 | 22,791,392 | 17,259,146 |
| 52 | 16,526,520,448 | 15,418,450,462 | 369,622,195,090 | 10,289,742 | 9,627,996 |
| 54 | 16,510,605,646 | 15,427,042,426 | 369,629,517,928 | 8,591,964 | 7,322,838 |
| 56 | 16,500,941,464 | 15,431,805,464 | 369,634,419,072 | 4,763,038 | 4,901,144 |
| 58 | 16,492,304,068 | 15,435,860,504 | 369,639,001,428 | 4,055,040 | 4,582,356 |
| 60 | 16,482,863,948 | 15,441,092,770 | 369,643,209,282 | 5,232,266 | 4,207,854 |
| 62 | 16,475,337,704 | 15,445,519,518 | 369,646,308,778 | 4,426,748 | 3,099,496 |
| 64 | 16,471,705,988 | 15,447,854,422 | 369,647,605,590 | 2,334,904 | 1,296,812 |
| 66 | 16,469,560,908 | 15,448,833,876 | 369,648,771,216 | 979,454 | 1,165,626 |
| 68 | 16,467,411,440 | 15,450,226,486 | 369,649,528,074 | 1,392,610 | 756,858 |
| 70 | 16,465,715,126 | 15,451,132,328 | 369,650,318,546 | 905,842 | 790,472 |
| 72 | 16,465,146,904 | 15,451,480,676 | 369,650,538,420 | 348,348 | 219,874 |
| 74 | 16,464,611,746 | 15,451,599,994 | 369,650,954,260 | 119,318 | 415,840 |
| 76 | 16,462,008,820 | 15,452,880,740 | 369,652,276,440 | 1,280,746 | 1,322,180 |
| 78 | 16,455,661,852 | 15,455,949,448 | 369,655,554,700 | 3,068,708 | 3,278,260 |
| 80 | 16,449,556,976 | 15,459,110,592 | 369,658,498,432 | 3,161,144 | 2,943,732 |
| 82 | 16,444,816,482 | 15,462,601,346 | 369,659,748,172 | 3,490,754 | 1,249,740 |
| 84 | 16,443,306,216 | 15,463,551,602 | 369,660,308,182 | 950,256 | 560,010 |
| 86 | 16,442,726,646 | 15,463,824,106 | 369,660,615,248 | 272,504 | 307,066 |
| 88 | 16,442,564,530 | 15,463,913,276 | 369,660,688,194 | 89,170 | 72,946 |
| 90 | 16,442,524,222 | 15,463,935,024 | 369,660,706,754 | 21,748 | 18,560 |
| 92 | 16,442,485,622 | 15,463,946,068 | 369,660,734,310 | 11,044 | 27,556 |
| 94 | 16,442,467,882 | 15,463,954,238 | 369,660,743,880 | 8,170 | 9,570 |
| 96 | 16,442,465,774 | 15,463,956,176 | 369,660,744,050 | 1,938 | 170 |
| 98 | 16,442,465,774 | 15,463,956,176 | 369,660,744,050 | 0 | 0 |
If a player cannot end their turn with a push, he or she will lose the game.
This occurs very rarely. Initially, it wasn't clear if there were any positions where a player cannot make any valid push (after using the two moves optimally), but it turns out there a few such cases. 648 to be exact (see solve-lost-output.txt), though most are variations of two basic patterns:
Example 1: here, red has 1 square piece that can move freely, but any push would push one of red's own pieces off the board.
Example 2: here, all of red's pieces are locked in and no moves are possible at all. The only possible push (h2-h3) would push red's own piece off the board.
It's clear that these are artificial positions that wouldn't come up naturally in a real game. The red player would never let their pieces get fenced in like this, and even if he would, the blue player would be able to win earlier by pushing a piece off the board, instead of waiting for red to lose on his turn.
The results from phase 0 (r0-bitcount.txt) show that of the 401,567,166,000 permutations, 340,787,248,692 (84.86%) can be won in 1 turn, and the remaining 60,779,917,308 (15.14%) are indeterminate. That means only about a sixth of the positions remain to be processed in phase 1.
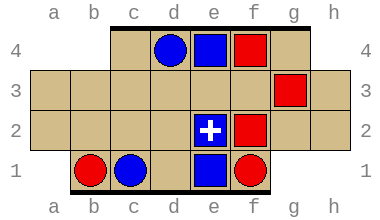
Most of these positions are really trivial, of course. Example:
The results from phase 1 (r1-counts.txt) show that of the 401,567,166,000 permutations, 6,233,064,422 (1.55%) are lost in 1 move (or 2 turns if we count each player's turn separately). This is 10.26% of the undecided positions after phase 1, with 54,546,852,886 (89.74%) positions remaining undecided.
Due to how these results are computed, this includes the 648 immediately lost positions, so very strictly speaking the count is only 6,233,063,774.
Most of these positions are still very simple. For example:
Here red (to move) can save the piece at a1 or the piece at f1, but not both, so blue will be able to win in the next turn.
For phase 2, I backpropagated the losses discovered in phase 1 using the backpropagate-losses tool (i.e., for every losing position, find the predecessors, and mark them winning, if they weren't before). This approach was faster than the forward search, probably because to prove a position is winning, we have to look at all successors and find one that is losing for the opponent, but since losses are relatively rare (1.55% after fase 1) most of these searches are exhaustive.
In this phase we discovered another 16,766,295,470 winning positions (see r2-wins-bitcount.txt) which is 4.18% of the total number of permutations, but 30.7% of the permutations that were still undecided after phase 1.
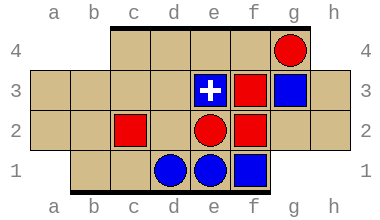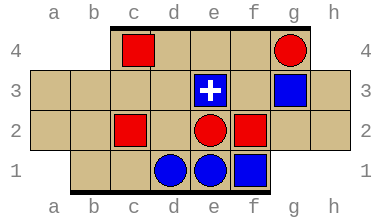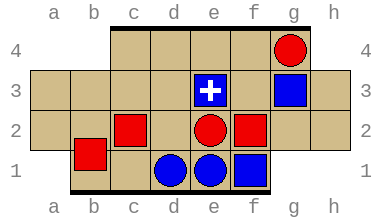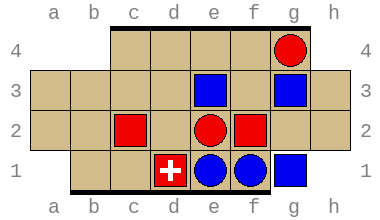
Some of the winning positions have quite interesting moves. An example:
After e4-g4, a3-e3, d3-e3:
Blue can't possible save the piece at h3.
After this phase, 37,780,557,416 positions (69.3%) remain undecided and will need to be re-evaluated in phase 3. Hopefully, this will be faster since to prove a LOSS we have to check that all successors are won by the opponent. If we find a tie, we can abort the search. Since there is still a large number of ties remaining, we can probably abort a lot of searches early, and all the searches that are exhaustive will discover an actual loss. This means either the phase will be fast, or we will discover a lot of lost positions, both of which are good.
In phase 3, we discovered 2,943,252,774 positions that were lost in 2 moves (or 4 turns). That's less than half of the number of losses discovered in phase 1, but still 7.8% of the ties remaining after phase 2.
The losses found this way are starting to become interesting. Consider the position below. It looks like red is in trouble with pieces on the edge at b1 and f1, but it seems that red should be able to salvage the situation with something like f1-e1,b1-f3,f3-f2:
The situation afterwards looks much better, with none of red's pieces on the edge, and blue's piece now in the danger zone on square f1! However, blue can respond with e4-d2,d4-b2,d1-c1:
Blue has trapped red's round piece at b1. Note that the move e4-d2 was necessary to protect the piece at f1.
In phase 4, we discovered 5,170,866,758 positions (14.8% of the remaining positions) that were won in 3 moves (or 5 turns). That's a lot less than in phase 2 (even relatively speaking), which suggests we are swowly getting closer to the fixed point.
There are 29,666,437,884 tied positions remaining (85.2% of the result of after phase 3, or 78.5% after phase 2).
In phase 5, we discovered 1,778,050,311 positions (6.0% of the remaining positions) that are lost in 3 moves (or 6 turns).
In phase 6, we discovered 2,255,991,948 positions (8.1% of the remaining positions) that are won in 4 moves (or 7 turns).
An example position is given below:
At first glance, it seems like red is in trouble, with pieces on the edge at a2, h2 and f1. The key to victory is to leave the square piece on f1 where it is, and instead move h2-d2, c2-b3, b3-c3 to trap blue's round piece at d1.
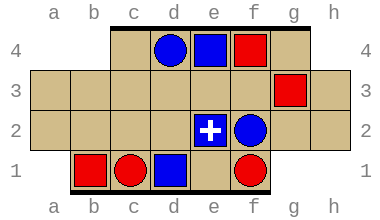
I believe every starting position where each player puts four pieces on the starting line (i.e., column D for Red, column E for Blue) leads to a tied position. That implies that if players start reasonably, all games are theoretically tied. However, it's easy to make a mistake during gameplay and create an opportunity for the opponent to win!
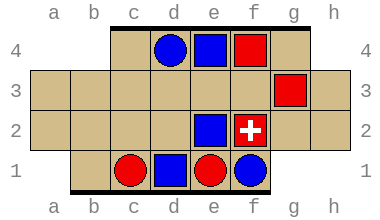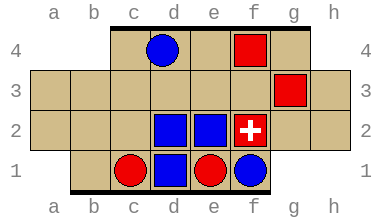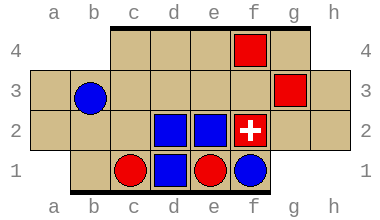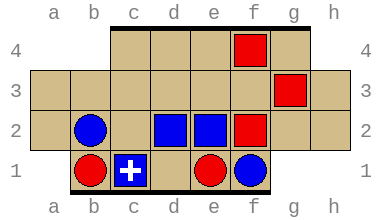
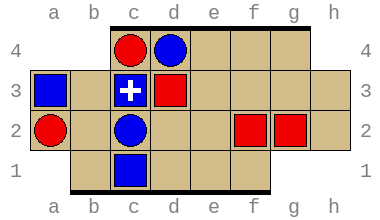
In the position below, red is to move. It looks like red is in trouble, with two pieces about to be pushed off the board. However, there is a way for red to survive at least one more turn! Can you tell how?