《数学分析》,史怀济,**科学大学,视频:共220讲,B站视频链接
因为此文件包含大量的公式,如果:
- 你在GitHub online查看,建议使用Chrome配合Chrome插件MathJax Plugin for Github以便查看排版后的LaTeX
- 你下载此Repo源文件到本地,建议使用Typora并开启(Inline Math)后查看。
1. 非负整数
方法一(反证法、韦达跳跃):
令 $$ k = \frac{a^2 + b^2}{ab + 1} $$
- 假设存在一个或更多不是完全平方数的解
$k$ 。 - 对特定
$k$ ,$(x, y) = (A,B)$ 是方程$x^2 + y^2 - mxy = 0$ 正整数解对。 - 由于
$x^2 + y^2 - mxy - m = 0$ 是关于 x,y 对称的方程,先设$A \ge B$ 。 - 再设原整数方程关于
$A$ 的二次方程,即为:$x^2 + b_1^2 - kBx- m = 0$,$x = A$ 是其中一个正整数根。利用韦达定理,可将另一根表示成$x_2 = kB - A$或是$x_2 = \frac{B^2 – k}{A}$。 - 从
$x_2$ 的第一个表示式可得$x_2$为整数,第二个表示式可得$x_2 \neq 0$,因为$k$不是完全平方数。进一步,从$\frac{x_2^2 + b^2}{x_2B+1}=k>0$可得$x_2$为正整数。 - 最后,从$A>B$可推出$x_2=\frac{B^2-k}{A}<A$,所以$x_2 + B < A + B$,与$A + B$为最小矛盾。
方法二(无穷递降法):
令
- 当
$a = b$ 时,
-
$k = \frac{2a^2}{a^2 + 1} = (2 - k)a^2 > 0$ ,即:$2 - k > 0, k \in (0, 2)$ ,因为$k$是整数,那么$k = 1$
- 当
$a \neq b$ ,设$a > b$ ,则
$k = \frac{a^2 + b^2}{ab + 1} > \frac{a^2 + b^2}{a^2 + 1} > 1$ - 根据题目条件,得到$a^2 - bka + b^2 - k = 0$, 且该方程必有正整数根
$a$ 。设另一根为$a_1$ 。得到$a^2 - bka + b^2 - k = 0, \tag{1}$ $a_1^2 - bka_1 + b^2 - k = 0, \tag{2}$
-
$(1), (2)$ 两式相减及相加(其实这是韦达定理),可以得到$a + a_1 = bk, \tag{3}$ $b^2 - k = a a_1, \tag{4}$ - 根据题目定义,$b, k$ 是整数,所以
$a_1$ 是整数。
- 接着证明
$a_1$ 的正负性:- 设
$a_1 \leq -1$ , 则$(a_1^2 + b^2) = k(a_1b + 1) \leq k(-b + 1) \leq 0$ 不成立,所以$a_1 \ge 0$ 。 - 所以
$0 \leq a_1 = \frac{b^2 - k}{a} < \frac{b^2}{a} < b < a$ - 如果
$a_1 = 0$ ,那么$k$为平方数,所以只用讨论$0 < a_1 < b < a$ 的情况
- 设
- 对
$k = \frac{a^2 + b^2}{ab + 1}$ 重复上面的推理,可知存在整数$b_1$满足$b > a_1 > b_1 \ge 0$ ,使得$k = \frac{a_1^2 + b_1^2}{a_1b_1 + 1}$ - 这样回到了原来的情况,不过这时有
$a > b > a_1 > b_1$ - 上述过程可以无限循环,最后必然有一个
$a_i = 0$ 或$b_i = 0$ 。不论任何情况,$k$都是一个平方数。
2.若$a_1 \leq a_2 \leq \cdots \leq a_n$,$b_1 \leq b_2 \leq \cdots \leq b_n$,证明Tchebycheff不等式: $$ \sum_{i=1}^n a_i \sum_{i=1}^n b_i \leq n\sum_{i=1}^n a_i b_i $$
证明:
由排序不等式可知,最大的和为顺序和:$a_1b_1+ \cdots + a_nb_n$
因此有:
$a_1b_1 + a_2b_2+ \cdots + a_nb_n = a_1b_1+ a_2b_2+ \cdots + a_nb_n$ $a_1b_1 + a_2b_2+ \cdots + a_nb_n \ge a_1b_2 + a_2b_3 + \cdots + a_nb_1$ $a_1b_1 + a_2b_2+ \cdots + a_nb_n = a_1b_3 + a_2b_4 + \cdots + a_nb_2$ $\vdots$ $a_1b_1+ a_2b_2 + \cdots + a_nb_n \ge a_1b_n + a_2b_1 + \cdots + a_nb_{n-1}$
将这$n$个不等式分边相加,同时对右边进行因式分解,便得到:
例四里用到 几何平均-算术平均不等式:
练习题 1.3 第3、4、5题
练习题 1.4 第3题
练习题 1.5 第1题
对于
是单调递增数列,并且有上界。
证明用到二项式定理有: $$ e_n = 1 + \sum_{k=1}^n \binom{n}{k} \frac{1}{n^k} $$
自然对数
基本列的定义:设${a_n}$是一列实数列。对任意给定的$\epsilon>0$,若存在$N\in N^$,使得当$m, n\in N^$且$m,n>N$时,有
数列收敛的充分必要条件是,数列是基本列。
引理:从任一数列中必可取出一个单调子列。
定理 Bolzano-Weierstrass定理:从任何有界的数列中必可选出一个收敛的子列。
定理:一个数列收敛的充分必要条件是它是基本列。
定义1.8.1:设$E$为一非空的有上界的集合,实数$\beta$满足一下两个条件:
- 对任何$x \in E$,有$x \leq \beta$;
- 对任意给定的$\epsilon >0$,必可找到一个$x_\epsilon \in E$,使得$x_\epsilon > \beta - \epsilon$
这时,称$\beta$为集合$E$的上确界,记作$\beta = \mathbb{sup} E$。
定义1.8.2:设$E$为一非空的有上界的集合,实数$\alpha$满足一下两个条件:
- 对任何$x \in E$,有$x \geq \alpha$;
- 对任意给定的$\epsilon >0$,必可找到一个$y\epsilon \in E$,使得$x\epsilon < \alpha + \epsilon$
这时,称$\alpha$为集合$E$的下确界,记作$\alpha = \mathbb{inf} E$。
定理1.8.1:非空的有上界的集合必有上确界;非空的有下界的集合必有下确界。
定义1.9.1:如果$A$是实数集,$\mathscr{J}=\left{I_{\lambda}\right}$是一个开区间族,其中$\lambda \in \Lambda$,这里的$\Lambda$称为指标集。如果 $$ A \subset \bigcup_{\lambda \in \Lambda} I_{\lambda} $$ 称开区间族${ I_\lambda }$是$A$的一个开覆盖,或者说${I_\lambda}$盖住了$A$。
定理1.9.1(紧致性定理):设$[a, b]$是一个有限闭区间,并且它有一个开覆盖${ I_\lambda }$,那么从这个开区间族中必可选取有限个成员(开区间)来,这有限个开区间所成的族任事$[a, b]$的开覆盖。也称为有限覆盖定理、Heine-Borel定理。
定义1.10.1:设${a_n}$是一个数列,$E$是由${a_n}$的全部极限点构成的集合。记
$$
a^{\space*}=\sup E, \quad a_{\space*}=\inf E
$$
-
$a^* \in E$ ; - 若$x > a^$,则存在$N \in N^$,使得当$n \geq N$时,有$a_n < x$;
-
$a^*$ 是满足前两条性质的唯一数。
定理1.10.2:设${a_n}$,${b_n}$是两个数列:
- $\liminf {n \rightarrow \infty} a{n} \leq\limsup {n \rightarrow \infty} a{n}$;
-
$\lim_{n \rightarrow \infty} a_{n}=a$ 当且仅当$\liminf {n \rightarrow \infty} a{n} = \limsup {n \rightarrow \infty} a{n} = a$; - 若$N$是某个正整数,当$n>N$时,$a_n \leq b_n$,那么
$$ \liminf {n \rightarrow \infty} a{n} \leq\liminf {n \rightarrow \infty} b{n}, \quad \limsup {n \rightarrow \infty} a{n} \leq\limsup {n \rightarrow \infty} b{n} $$
定理1.10.3:对于数列${a_n}$,定义$\alpha_n=\inf_{k\geq n}a_k$,
-
${\alpha_n}$ 是递增数列,${\beta_n}$是递减数列; - $\lim_{n\rightarrow \infty}\alpha_n = a_$, $\lim_{n\rightarrow \infty}\beta_n = a^$。
定理1.11.1
定义 2.1.1:设$A, B$s是两个集合,如果$f$是一种规律,使得对$A$中的每一个元素$x$,$B$中唯一确定的元素——记作$f(x)$——与$x$对应,则称$f$是一个$A$到$B$的映射,用 $$ f: A \rightarrow B $$ 来表示。集合$A$叫作映射$f$的定义域;$f(x) \in B$叫作$x$在映射$f$之下的像或$f$在$x$的值。
定义2.1.2:相等:设$f: A \rightarrow B$,且$g: A \rightarrow B$。如果对任何$x \in A$,均有$f(x) = g(x)$,则称映射$f$与$g$相等,记为$f=g$。
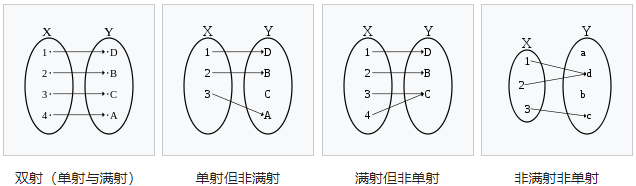
定义2.1.3:满射:设$f: A \rightarrow B$,如果$f(a)=B$,则称$f$是从$A$到$B$上的满射,也就是说,$B$中的任何元素都是$A$中某一元素在$f$之下的像。
定义2.1.4:单射:设$f: A \rightarrow B$,如果当$x, y \in A$,且$x \neq y$时,有$f(x) \neq f(y)$,则称$f$为单射。
定义2.1.5:一对一:设$f: A \rightarrow B$,既是单射又是满射,则称映射$f$是一对一的,这时,也说$f$在集合$A$与$B$之间建立一个一一对应。
逆映射:$f^{-1} : B \rightarrow A$,其规律是:如果$y=f(x)$,则$f^{-1}(y)=x$。
定义2.1.6:设$f : A \rightarrow B, f \subset B$,则$A$的子集 $$ f^{-1}(F) = {x \in A: f(x) \in F} $$ 叫做$F$的原像。
定义2.1.7:设映射$f : B \rightarrow C$,映射$g$的定义域为$A$。当$x \in A_1=g^{-1}(B)$时,定义映射 $$ f \circ g(x) = f(g(x)) $$ 显然,$f \circ g : A_1 \rightarrow C$,称为映射$f$和$g$的复合。
设$A$与$B$两个集合,如果存在一个从$A$到$B$的一对一映射,称集合$A$与$B$有相同的“势”或有相同的“基数”,称$A$与$B$等价。用$A \sim B$表示。这种关系具有以下性质:
- 自反性:$A \sim A$
- 对成性:$A \sim B$且$B \sim A$
- 传递性:若$A \sim B$且$B \sim C$,则$A \sim C$
定义2.2.1:令$N^*$为正整数的全体,且
- 有限集:如果存在一个正整数$n$,使得集合$A \sim N_{n}$,那么$A$叫做有限集。
- 无限集:如果集合$A$不是有限集,则称$A$为无限集。
- 可数集:若$A \sim N_{n}$,则称$A$为可数集。
- 不可数集:若$A$既不是有限集,也不是可数集,则称$A$为不可数集。
- 至多可数:若$A$是有限集或者$A$是可数集,则称$A$是至多可数的。
定理2.2.1:可数集$A$的每一个无限子集是可数集。
定理2.2.3:$\mathbb{R}$中的全体有理数是可数的。
定理2.2.4:$[0, 1]$上的全体实数是不可数的。
函数是一类特殊的映射,如果对映射$f: X \rightarrow Y$,$X$与$Y$都是由实数组成,则$f$称为一个函数。
分段函数:由多个公式联合起来表示的函数
函数的和:设$f$和$g$是两个函数,定义域分别为$A$和$B$,那么在$A \cap B$上,$f+g$称作$f$与$g$的和,写作: $$ (f+g)(x)=f(x)+g(x), x \in A \cap B $$ 类似的,可以定义$f$与$g$的差、积、商: $$ \begin{array}{c}{(f-g)(x)=f(x)-g(x)} \ {\quad(f g)(x)=f(x) g(x)} \ {\quad\left(\frac{f}{g}\right)(x)=\frac{f(x)}{g(x)}}\end{array} $$ 反函数:设函数$f$在$X$与$Y$之间建立了一个一一对应,那么有逆映射$f^{-1}: Y \rightarrow X$,称$f^{-1}$为$f$的反函数。
定义2.3.1:递增(递减)函数:对于函数$f : X \rightarrow Y$,如果对于任何$x_1, x_2 \in X$,只要
定义2.3.1(严格)单调函数:在$X$上的(严格)递增或(严格)递减函数。
定理2.3.1:设函数$f$在其定义域$X$上是严格递增(递减)的,那么反函数$f^{-1}$必存在,$f^{-1}$的定义域为$f(X)$,$f^{-1}$在这一集合上也是严格递增(递减)的。
2、反证法:如果$f$没有不动点,那么$f \circ f$也没有不动点;如果$f$有多个不动点,那么$f \circ f$也有多个不动点。
3、反证法:假设存在$f(a) = d, f(d) = a, d \neq b$,那么$d$也是不动点,与题目矛盾
4、(1)$f(x) = x, f(x) = -x$ (2)$f(x) = x$
7、以任何正数为周期,那么对于任意$l$有$f(x + l) = f(x)$
8、(1)$\sin()$的周期是
(2)
定义2.4.1 函数极限:设函数$f$在点$x_0$的附近有定义,但$x_0$这一点自身可以是例外。设$l$是一个实数,如果对任意给定的$\epsilon > 0$,存在一个$\delta >0$,使得对一切满足不等式$0<|x-x_0|<\delta$的$x$,均有
$$
|f(x)-l|<\epsilon
$$
则称当$x$趋于点$x_0$时函数$f$有极限
定理2.4.3:若$f$在$x_0$处有极限,那么$f$在$x_0$的一个近旁是有界的。也就是,存在整数$M, \delta$,使得当$0<\left|x-x_{0}\right|<\delta$时,$ f(x)|<M$。
定理2.4.4:$\lim {x \rightarrow x{0}} f(x)$与$\lim {x \rightarrow x{0}} g(x)$都存在时,那么有:
- $\lim {x \rightarrow x{0}}(f \pm g)(x)=\lim {x \rightarrow x{0}} f(x) \pm \lim {x \rightarrow x{0}} g(x)$
- $\lim {x \rightarrow x{0}}fg(x)=\lim {x \rightarrow x{0}} f(x) \cdot \lim {x \rightarrow x{0}} g(x)$
- $\lim {x \rightarrow x{0}}\frac{f}{g}(x)=\frac{\lim {x \rightarrow x{0}} f(x)}{\lim {x \rightarrow x{0}} g(x)}$,其中$\lim {x \rightarrow x{0}} g(x) \neq 0$
定理2.4.5:设函数$f, g$与$h$在点$x_0$的近旁(点$x_0$自身可能是例外)满足不等式 $$ f(x) \leq h(x) \leq g(x) $$ 如果$f, g$在点$x_0$有相同的极限$l$,那么$h$点$x_0$也有极限$l$。
定理2.4.6:设存在$r>0$,使得当$0<|x-x_0|<r$时,不等式$f(x)\leq g(x)$成立,又设在$x_0$出这两个函数都有极限,那么 $$ \lim_{x \rightarrow x_0}f(x) \leq \lim_{x \rightarrow x_0}g(x) $$ 定理2.4.7:函数$f$在$x_0$有极限,必须且只需对任意给定的$\epsilon > 0$,存在$\delta > 0$,使得对任意的$x_1, x_2 \in B_\delta(\hat x_0)$,都有$|f(x_1)-f(x_2)|<\epsilon$。
定理2.4.8:设$\lim_{x \rightarrow x_0}f(x)=l, \lim_{x \rightarrow t_0}g(t)=x_0$,如果在$t_0$的某个领域$B_{\eta}(t_0)$内$g(t) \neq x_0$,那么 $$ \lim_{t \rightarrow t_0} f(g(t))=l $$ 定义2.4.2:设函数$f$在$(x_0, x_0+r)$上有定义。设$l$是一个给定的实数,若对任意给定的$\epsilon > 0$,存在一个$\delta \in (0, r)$,使得$0 < x-x_0 < \delta$时,有 $$ |f(x) - l| < \epsilon $$ 则称$l$为$f$在$x_0$处的右极限,表示为 $$ l=\lim_{x \rightarrow x^+_0}f(x) $$ 右极限通常记作$f(x_0+)$,类似地,可以定义$f$在$x_0$处的左极限$f(x_0-)$。
定理2.4.9:设函数$f$在$x_0$的某个领域内($x_0$可能是例外)有定义,那么$\lim_{x \rightarrow x_0} f(x)$ 存在的充分必要条件是 $$ f(x_0+) = f(x_0-) $$ 例子: $$ \lim_{x \rightarrow 0}\frac{\sin x}{x}=1 $$
11、(3)$x^{m-1}+x^{m-2}+\cdots+1=m$
(4)同理,$m/n$
(5)$\frac{1}{\sqrt{1+x}+1}=\frac{1}{2}$
(7)
(8)$=\lim_{x \rightarrow 1}\left(\frac{x-1}{x-1}+\frac{x^2-1}{x-1}+\cdots+\frac{x^m-1}{x-1}\right)=1+2+\cdots+m=\frac{(1+m)m}{2}$
定义2.5.1:设$l$是一确定实数,表达式 $$ \lim_{x \rightarrow \infty} f(x)=l $$ 的意思是,对任意给定的$\epsilon > 0$,存在一个正数$A$,当$x$满足$|x|>A$时,有$|f(x)-l|<\epsilon$。这时,我们说“当x趋向于无穷时,函数$f$有极限$l$”。
定义2.5.2:对任意给定的$\epsilon > 0$,存在一个正数$A>0$,使得当$x<-A$时,有 $$ |f(x) - l| < \epsilon $$
在这种情况下,我们说“在负无穷处函数$f$有极限$l$”,记作 $$ f(-\infty) = \lim_{x\rightarrow -\infty}f(x)=l $$ 定理2.5.1:$\lim_{x \rightarrow \infty} f(x)=l$ 当且仅当 $$ f(-\infty) = \lim_{x\rightarrow -\infty}f(x)=l, f(+\infty) = \lim_{x\rightarrow +\infty}f(x)=l $$ 同时成立。
定义2.6.1:设$x_0$是一个实数,函数$f(x)$在$x_0$的一个近旁(可能除$x_0$之外)有定义。如果对任意给定的正数A,存在$\delta>0$,使得$0<|x-x_0|<\delta$时,有$|f(x)|>A$,则称“当x趋向于$x_0$时,函数$f$趋向于**无穷大**”,记作 $$ \lim_{x\rightarrow x_0}f(x)=\infty, $$ 或者 $$ f(x)\rightarrow\infty \quad (x\rightarrow x_0) $$
类似的,如果$\lim f(x)=0$,则称“在该过程中,$f$是一个**无穷小(量)**”。
定义2.6.2:设当$x\rightarrow x_0$时,$f$与$g$都是无穷小,并且$g$在$x_0$的一个充分小的近旁(除$x_0$外)不取零值。
(1)如果$\lim_{x\rightarrow x_0}\frac{f(x)}{g(x)}=0$,那么称$f$是比$g$更高阶的无穷小;
(2)如果$\lim_{x\rightarrow x_0}\frac{f(x)}{g(x)} \neq 0$,那么称$f$是和$g$同阶的无穷小;
(3)如果(2)中的极限值$l=1$,那么称$f$与$g$石等阶的无穷小,记作$f \sim g \quad (x \rightarrow x_0)$。
类似的,如果$f, g$都是无穷大:
(1)如果$\lim_{x\rightarrow x_0}\frac{f(x)}{g(x)}=0$,那么称$g$是比$f$更高阶的无穷大;
(2)如果$\lim_{x\rightarrow x_0}\frac{f(x)}{g(x)} \neq 0$,那么称$f$是和$g$同阶的无穷大;
定理2.6.1:如果当$x\rightarrow x_0$($x_0$可以是$\pm \infty$)时,$f,g$等价的无穷小或无穷大时,那么:
(1)$\lim_{x\rightarrow x_0}f(x)h(x)=\lim_{x\rightarrow x_0}h(x)f(x)$
(1)$\lim_{x\rightarrow x_0}\frac{f(x)}{h(x)}=\lim_{x\rightarrow x_0}\frac{g(x)}{h(x)}$
定义2.6.3:设函数$f,g$在$x_0$的近旁($x_0$除外)有定义,并且$g(x)\neq 0$:
(1)当$x\rightarrow x_0$时,若比值$f(x)/g(x)$保持有界,即存在正常数$M$,使得$|f(x)|\leq M|g(x)|$成立,就用$f(x)=O(g(x))(x\rightarrow x_0)$来表示;
(2)当$x\rightarrow x_0$时,若比值$f(x)/g(x)$是一个无穷小,即$\lim_{x\rightarrow x_0}\frac{f(x)}{g(x)}=0$,就用$f(x)=o(g(x))(x\rightarrow x_0)$表示。
定义2.7.1:设$f:[a,b]\rightarrow R$,我们称函数$f$在点$x_0\in (a,b)$连续,如果 $$ \lim_{x\rightarrow x_0}f(x)=f(x_0) $$ 也就是说,对任意给定的$\epsilon >0$,存在一个适当的$\delta >0$,使得当$|x-x_0|<\delta$时,有 $$ |f(x) - f(x_0)|<\epsilon $$
存在处处不连续的函数(如Dirichlet函数),也存在只在一点连续的函数。
定义2.7.2:如果$f(x_0+)=f(x_0)$,则函数在$x_0$处右连续,如果$f(x_0-)=f(x_0)$,则函数左连续。
定理2.7.1:如果函数$f$与$g$在$x_0$处连续,那么$f\pm g$与$fg$在$x_0$处连续,进一步,若$g(x_0)\neq 0$,则$f/g$也在$x_0$处连续。
定理2.7.2:如果函数$g$在$t_0$处连续,记作$g(t_0)$为$x_0$,如果函数$f$在$x_0$处连续,那么复合函数$f \circ g$在$t_0$处连续。
定义2.7.3:设I是一个开区间,例如$(a, b), (a, +\infty), (-\infty, b), (-\infty, +\infty)$。如果函数$f$在$I$上的每一点都连续,则称$f$在$I$上连续,是指$f$在$(a,b)$上连续,并且在$a$点处右连续,同时在$b$点处左连续。人们也称$f$是$I$上的**连续函数**。不论区间$I$是开区间或闭区间,有限或无穷的,用$C(I)$记$I$上连续函数的全体。
定理2.7.3:设$f$是在区间$I$上严格递增(减)的连续函数,那么$f^{-1}$是$f(I)$上的严格递增(减)函数。
初等函数:多项式函数、幂函数、指数函数、对数函数、三角函数、反三角函数,以及经过它们有限次的四则运算、有限次复合所形成的函数,统称初等函数。
定理2.7.4:初等函数在它们各自的定义域上都是连续的。
设$x_0$是函数$f$定义域中的一点,如果$f$在$x_0$连续,则称$x_0$为f的**连续点,否则为间断点**。
定义2.7.4:设$x_0$是函数$f$的间断点:
- 如果$f(x_0+)$与$f(x_0-)$存在,且是有限的数,但$f(x_0+) \neq f(x_0-)$,那么$x_0$为$f$的一个**跳跃点。差值$|f(x_0+) - f(x_0-)|>0$称为$f$在这一点的跳跃**。
- 如果$f(x_0+)$与$f(x_0-)$存在且有限,并且$f(x_0+) = f(x_0-)$但是不等于$f(x_0)$,则称$x_0$为$f$可去间断点。
- 如果$f(x_0+)$与$f(x_0-)$中至少有一个不存在或者不是有限的数,那么$x_0$叫做$f$的**第二类间断点**。
- 跳跃点和可去间断点统称为$f$的**第一类间断点**。
定理2.7.5:设$f$是区间$(a, b)$上的递增(减)函数,则$f$的间断点一定是跳跃点,而且跳跃点集是至多可数的。
如果函数$f$在$x_0$处连续,那么 $$ \lim_{x\rightarrow x_0}f(x)=f(x_0) $$ 函数$f$在$x_0$处连续的事实可以表示为 $$ \lim_{x\rightarrow x_0}f(x)=f(\lim_{x\rightarrow x_0}x) $$ 极限的计算:
$\lim_{x\rightarrow 0}(1+x)^{1/x}=\lim_{y\rightarrow \infty}(1+1/y)^y=e$
幂指函数:$u(x)^{v(x)}\quad (u(x)>0)$
- 当$u, v$时连续函数时,幂指函数也是连续函数。
定义2.9.1:如果对任意给定的$\epsilon>0$,总是存在一个$\delta>0$,使得当$x_1, x_2 \in I$且$|x_1-x_2|<\delta$时,有$|f(x_1)-f(x_2)|<\delta$,则称函数$f$在区间$I$上是**一致连续**的。
不是一致连续:当且仅当存在一个$\epsilon_0 > 0$,对每一个$n\in N^*$,都可以在$I$中找到两个点,记为$s_n$和$t_n$,使得虽然有$|s_n-t_n|<1/n$,但是 $$ |f(s_n)-f(t_n)\geq \epsilon_0. $$
定理2.10.1:设函数$f$在$[a, b]$上连续,那么$f$在$[a, b]$上一致连续。(注意,此区间必须是有界的)
定理2.10.2:有界闭区间上的连续函数必在该区间上有界。
定理2.10.3:设$f$在$[a, b]$上连续,记 $$ M=\sup_{x\in [a, b]}f(x), \quad m = \inf_{x\in [a, b]}f(x), $$ 则必存在$x^, x_ \in [a, b]$,使得 $$ f(x^)=M, \quad f(x_) = m. $$ 定理2.10.4(零值定理):设$f$在$[a, b]$上连续,如果$f(a)f(b)<0$,则必存在一点$c\in (a, b)$,使得$f(c)=0$。
定理2.10.5(介值定理):设$f$是在$[a, b]$上非常值的连续函数,$\gamma$是介于$f(a)$与$f(b)$之间的任何实数,则必存在$c \in (a, b)$,使得$f(c) = \gamma$。
推论2.10.1:设非常数值函数$f$在$I=[a, b]$上连续,那么$f$的值域$f(I)$是一个闭区间。
定义2.11.1:令$E={l \in R_{\infty}:存在数列x_n\in B_{\delta}(\tilde{x}), x_n \rightarrow x_0, 使得f(x_n)\rightarrow l}$
这是一个非空集合,设$a^=\sup E, a_=\inf E$,分别称它们为
-
$a^{*} \in E$ ; - 若$y > a^*$,则存在$\delta > 0$,使得当
$0 < |x - x_0| < \delta$ 时,$f(x) < y$; -
$a^*$ 是满足前述条件性质唯一的数。
定理2.11.2:设$f, g$在$I$上有定义,那么:
-
$\lim_{x \rightarrow x_0} \inf f(x) \leq \lim_{x \rightarrow x_0} \sup f(x)$ ; -
$\lim_{x \rightarrow x_0} f(x) = a$ , 当且仅当$\lim_{x \rightarrow x_0} \inf f(x) = \lim_{x \rightarrow x_0} \sup f(x) = a$; - 若当$x \in I$时,$f(x) \leq g(x)$成立,则
自然界中,许多现象,是有严格的因果关系所支配的。例如月亮的阴晴圆缺、四季的更迭、日食和月食的发生……对这一类完全由因果关系支配的系统进行一般研究,自然有重大意义。这种完全由因果关系所制约的系统,通常叫做**决定性系统。研究决定性系统的数学分支称为动力系统理论**。
设$I$是任意一个区间,函数$f: I \rightarrow I$。将$f$反复地复合,产生$f^2(x) = f \circ f(x)$,一般地,$f^n(x) = f \circ f^{n-1}(x) (n \geq 3)$。规定$f^0(x) = x$,即表示恒等映射;$f^1(x) = f(x)$。称$f^n$为$f$的**第n次迭代**。
对任意固定的$x \in I$,考虑序列 $$ x, f(x), f^2(x), \cdots, f^n(x), \cdots. $$ 如果正整数$m$使得$f^m(x) = x$,乘$m$为点$x$的一个周期,称$x$为$f$的一个周期点。
那么$m$的任何正整数倍一定也是$x$的一个周期。
对于上述序列叫做点$x$的$n$周期轨。
定义2.12.1:设$f$施区间$I$到自身的连续映射,$f$满足下列条件:
(1). f的周期点的最小周期没有上界; (2). 存在I的不可数子集S,满足: (a) 对任何$x, y \in S, x \neq y$,有 $$ \lim_{n \rightarrow \infty}\sup |f^n(x) - f^n(y)| > 0; $$ (b) 对任何$x, y \in S$,有 $$ \lim_{n \rightarrow \infty}\inf |f^n(x) - f^n(y)| = 0; $$ 这时称$f$描述的系统为混沌系统。
定义 3.1.1(可导的定义):设函数$f$在点$x_0$的近旁有定义,如果极限 $$ \lim_{h\rightarrow 0} \frac{f(x_0 + h) - f(x_0)}{h} $$ 存在且有限,则称这个极限值为$f$在点$x_0$的导数,记作$f'(x_0)$,并称函数$f$在点$x_0$可导。
定义 3.1.2(左右导数定义):设函数$f$在点$x_0$的右边$[x_0, x_0+r]$上有定义。若极限 $$ \lim_{h\rightarrow 0} \frac{f(x_0 + h) - f(x_0)}{h} $$ 存在且有限,则称此极限为$f$在点$x_0$的右导数,记作$f'+(x_0)$。类似地,可定义$f$在点$x_0$的左导数$f'-(x_0)$。
函数$f$在点$x_0$可导的充分必要条件是,在点$x_0$左、右导数存在且相等。
定理 3.1.1(可导与连续):若函数$f$在点$x_0$可导,则$f$必在点$x_0$连续。
定义 3.1.3(在区间可导):如果函数$f$在开区间$(a, b)$中每一点可导,则称$f$在$(a, b)$可导;如果$f$在$(a, b)$可导,并且在点$a$处有右导数,在点$b$处有左导数,则称$f$在闭区间$[a, b]$可导。
定理 3.2.1(求导的四则运算):设函数$f$和$g$在点$x$处可导,则$f \pm g$,
- (1)
$(f \pm g)'(x) = f'(x) \pm g'(x)$ - (2)
$(fg)'(x) = f'(x)g(x) + f(x)g'(x)$ - (3)
$\left(\frac{f}{g}\right)'(x) = \frac{f'(x)g(x) - f(x)g'(x)}{g^2(x)}$
定理 3.2.2(链式法则):设函数$\phi$在点$t_0$处可导,函数$f$在点$x_0 = \phi(t_0)$处可导,那么复合函数$f \circ \phi$在点$t_0$处可导,并且 $$ (f \circ \phi)'(t_0) = f'(\phi(t_0)) \phi'(t_0) $$ 上述法则可以推广到三个或更多组合的复合函数。
定理 3.2.3(反函数的导数):设$y = f(x)$在包含$x_0$的区间$I$上连续且严格单调。如果它在$x_0$处可导,且$f'(x_0) \neq 0$,那么它的反函数$x = f^{-1}(y)$在$y_0 = f(x_0)$处可导,并且 $$ (f^{-1})'(y_0) = \frac{1}{f'(x_0)} $$ 导数的几何意义:函数$f$在点$x_0$处的导数$f'(x_0)$,可以看成平面曲线$y=f(x)$在点$(x_0, f(x_0))$处的切线的斜率。
常见的求导公式: $$ c' = 0 \ (x^\mu)' = \mu x^{\mu-1} \ (e^x)' = e^x \ (a^x)' = a^x\ln a \ (\log_a x)' = \frac{1}{x \ln a} \ (\ln x)' = \frac{1}{x} \ (\sin x)' = \cos x \ (\cos x)' = -\sin x \ (\tan x)' = \frac{1}{\cos^2x} \ (\cot x)' = -\frac{1}{\sin^2x} \ (\arcsin x)' = \frac{1}{\sqrt{1-x^2}} \ (\arccos x)' = -\frac{1}{\sqrt{1-x^2}} \ (\arctan x)' = \frac{1}{1+x^2} \ (\text{arccot }x)' = -\frac{1}{1+x^2} $$
设函数$f$在区间$I$上可导,那么$f'(x)(x \in I)$在$I$上定义了一个函数$f'$,称之为$f$的导函数。
如果$f'$在$I$上可导,那么$f'$的导函数$(f')'$记作$f''$,称为$f$的二阶导函数。
对于任何正整数$n \in \N^*$,可以定义$f$的$n$阶导函数
定理 3.3.1(Leibniz 莱布尼茨)设函数$f$与$g$在区间$I$上都有$n$阶导数,那么乘积$fg$在区间$I$上也有$n$阶导数,并且 $$ (fg)^{(n)} = \sum^n_{k=0} \begin{pmatrix} n\ k \end{pmatrix} f^{(n-k)}g^{(k)} $$ 这里$f^{(0)} = f, g^{(0)} = g$。其中组合系数$\begin{pmatrix} n\ k \end{pmatrix}=\frac{n!}{k!(n-k)!} \quad(k=0,1,\cdots,n).$
定义 3.4.1:设函数$f:(a, b) \rightarrow R$。如果对点$x_0 \in (a, b)$,存在$\delta > 0$,使得$\Delta = (x_0 - \delta, x_0 + \delta) \subset (a, b)$,并且当$x \in \Delta$时,$f(x_0) \ge f(x)$,即$f(x_0)$是$f$在$\Delta$上的最大值,那么称$f(x_0)$是$f$在$(a, b)$上的一个极大值,$x_0$称为$f$的一个极大值点。
类似地,可以定义$f$在$(a, b)$上的极小值和极小值点。
极小值和极大值统称极值,极小值点和极大值点统称极值点。
定理 3.4.1(Fermat):若函数$f$在机极值点$x_0 \in (a, b)$处可导,则必有$f'(x_0) = 0$。
定义3.4.2:满足$x_0 \in (a, b)$且$f'(x_0) = 0$,则称$x_0$为函数$f$的一个驻点。
定理3.4.2(Rolle 罗尔):设函数$f$在$[a, b]$上连续,在$(a, b)$内可导,且$f(a) = f(b)$,那么存在一点$\xi \in (a, b)$,使得$f'(\xi) = 0$。
引理3.4.1:设函数$f$与$\lambda$在$[a, b]$上连续,在$(a, b)$上可导,并且$\lambda(a) = 1, \lambda(b) = 0$,则必存在一点$\xi \in (a, b)$,使得
$$
f'(\xi) = \lambda'(\xi)(f(a) - f(b))
$$
定理3.4.3(Lagrange):设$f$在$[a, b]$上连续,在$(a, b)$上可导,则存在一点$\xi \in (a, b)$,使得
$$
\frac{f(b) - f(a)}{b - a} = f'(\xi)
$$
推论3.4.1:设函数$f$在$[a, b]$上连续,在$(a, b)$上可导,则函数$f$在$[a, b]$上为常数的充分必要条件是
定理3.4.4(Cauchy):设函数$f$和$g$在区间$[a, b]$上连续,在区间$(a, b)$上可导,且当$x \in (a, b)$时,$g'(x) \neq 0$,这时必存在一点$\xi \in (a, b)$,使得 $$ \frac{f(b) - f(a)}{g(b) - g(a)} = \frac{f'(\xi)}{g'(\xi)} $$ 定理3.4.5(Darboux达布):如果$f$在$[a, b]$上可导,那么:
- 导函数$f'$可以取到$f'(a)$与$f'(b)$之间的一切值
-
$f'$ 无第一类间断点
定理3.5.1:设函数$f$在区间$[a, b]$上连续,在$(a, b)$上可导,那么$f$在$[a, b]$上递增(减)的充分必要条件是,$f' \ge 0 (\le 0)$在区间$(a, b)$上成立。
定理3.5.2:设函数$f$在$[a, b]$上连续,在$(a, b)$上可导。如果$f' > 0 (f' < 0)$在$(a, b)$上成立,那么$f$在$[a, b]$上是严格递增(严格递减)的。
定理3.5.3:设函数$f$在$[a, b]$上连续,在$(a, b)$内除了有限点之外,有正(负)的导数,那么$f$在$[a, b]$上严格递增(严格递减)。
定理3.5.4:设函数$f$在$[a, b]$上连续,在$(a, b)$上可导,那么$f$在$[a, b]$上严格递增(严格递减)的充分必要条件是:
- 当$x \in (a, b)$时,$f' \ge 0 (f' \le 0)$;
- 在$(a, b)$的任何开子区间上
$f' \neq 0$ 。
定理3.5.5:设函数$f$在$[a, b]$上连续,$x_0 \in (a, b)$:
- 如果存在正数$\delta > 0$,使得在$(x_0 - \delta, x_0)$上$f' > 0$,而在$(x_0, x_0 + \delta)$上$f' < 0$,那么$f(x_0)$是$f$的一个严格极大值,所谓“严格极大值”是指,当$0 < |x-x_0| < \delta$时,$f(x) < f(x_0)$。
- 如果存在正数$\delta > 0$,使得在$(x_0 - \delta, x_0)$上$f' < 0$,而在$(x_0, x_0 + \delta)$上$f' > 0$,那么$f(x_0)$是$f$的一个严格极小值,所谓“严格极小值”是指,当$0 < |x-x_0| < \delta$时,$f(x) > f(x_0)$。
定理3.5.6:设函数$f$在$[a, b]$上连续,$x_0 \in (a, b)$是$f$的一个驻点,进一步,设$f''(x_0)$存在,那么:
- 当$f''(x_0) < 0$时,$f(x_0)$是$f$的一个严格极大值;
- 当$f''(x_0) > 0$时,$f(x_0)$是$f$的一个严格极小值;
凸函数(Convex function):设函数$f$在区间$I$上有定义,如果对任何$x_1, x_2 \in I, x_1 \neq x_2$,以及任意的$\lambda_1, \lambda_2 > 0$,且$\lambda_1 + \lambda_2 = 1$,都有 $$ f(\lambda_1 x_1 + \lambda_2x_2) \leq \lambda_1f(x_1) + \lambda_2f(x_2) $$ 则$f$为$I$上的凸函数。如果上述不等式对任何的$x_1 \neq x_2, \lambda_1, \lambda_2 > 0 (\lambda_1 + \lambda_2 = 1)$不等号总成立,那么$f$在$I$上是严格凸函数。
定理3.5.9:函数$f$在$I$上市凸函数,当且仅当对任何$(x_1, x_2) \subset I$及任何$x \subset (x_1, x_2)$有 $$ \frac{f(x) - f(x_1)}{x - x_1} \leq \frac{f(x_2) - f(x_1)}{x_2 - x_1} \leq \frac{f(x_2) - f(x)}{x_2 - x} $$ 如果$f$是严格凸函数,则上述是严格的不等号。
定理3.5.10:设$f$在$[a, b]$上连续,在$(a, b)$上可导,则$f$在$[a, b]$上为凸函数(严格凸函数)的一个充分必要条件是,$f'$在$(a, b)$上递增(严格递增)。
定理3.5.11:设函数$f$在$[a, b]$上连续,在$(a, b)$上有二阶导数,则$f$在$[a, b]$上为凸函数的充分必要条件是,$f'' \ge 0$在$(a, b)$上成立;而$f$在$[a, b]$上为严格凸函数的充分必要条件是,$f'' \ge 0$在$(a, b)$上成立,并且在$(a, b)$的任何子区间内$f''$不恒等于0.
定理3.6.1(L'Hospital洛必达):设$f, g$在$(a, b)$上可导,并且$g(x) \neq 0$对$x \in (a, b)$成立,又设 $$ \lim_{x \rightarrow a^+} f(x) = \lim_{x \rightarrow a^+} g(x) = 0 $$ 在这些条件下,如果极限$\lim_{x \rightarrow a^+} \frac{f'(x)}{g'(x)}$存在(或为$\infty$),那么便有 $$ \lim_{x \rightarrow a^+} \frac{f(x)}{g(x)} = \lim_{x \rightarrow a^+} \frac{f'(x)}{g'(x)}. $$ 定理3.6.2:设函数$f, g$在$(a, +\infty)$上可导,并且$g(x) \neq 0$对$x \in (a, +\infty)$成立,又设 $$ \lim_{x \rightarrow +\infty} f(x) = \lim_{x \rightarrow +\infty} g(x) = 0, $$ 如果极限$\lim_{x \rightarrow +\infty} \frac{f'(x)}{g'(x)}$存在(或为$\infty$),有 $$ \lim_{x \rightarrow a^+} \frac{f(x)}{g(x)} = \lim_{x \rightarrow a^+} \frac{f'(x)}{g'(x)}. $$ 定理3.6.3:设函数$f, g$在$(a, b)$上可导,并且$g(x) \neq 0$,且 $$ \lim_{x \rightarrow a^+}g(x) = \infty $$ 如果极限$\lim_{x \rightarrow a^+} \frac{f'(x)}{g'(x)}$存在或为$\infty$,那么 $$ \lim_{x \rightarrow a^+} \frac{f(x)}{g(x)} = \lim_{x \rightarrow a^+} \frac{f'(x)}{g'(x)}. $$
定义3.7.1(拐点):设函数$f$在$x_0$的两旁(包括$x_0$在内)有定义,在$x_0$的一侧图像$y = f(x)$时严格凸的,另一侧是严格凹的,那么称$x_0$是$f$的一个拐点。
定义3.7.2(渐近线):(1)如果$\lim_{x \rightarrow +\infty}f(x) = a$或$\lim_{a \rightarrow -\infty}f(x) = b$,则称$y = a$或$y = b$为$y = f(x)$的一条水平渐近线。
(2)如果$\lim_{x \rightarrow x_0^+}f(x) = \pm \infty$或$\lim_{x \rightarrow x_0^-}f(x) = \pm \infty$,则称$x = x_0$为$y = f(x)$的一条垂直渐近线。
(3)如果$a \neq 0$,使得$\lim_{x \rightarrow +\infty}(f(x) - (ax + b)) = 0$或$\lim_{x \rightarrow -\infty}(f(x) - (ax + b)) = 0$,则称$y = ax + b$为$y = f(x)$的一条斜渐近线。
作图的步骤:
- 确定函数的定义域
- 判断函数是否有奇偶性、周期性及其他对称性
- 确定函数的增减区间及极值点
- 确定函数的凹凸区间及拐点
- 确定函数是否有渐近线
- 求出一些特殊点的值
定义4.1.1(可微、微分):设函数$f$在$(a, b)$上有定义,且$x_0 \in (a, b)$,如果存在一个常数$\lambda$使得 $$ f(x_0+\Delta x) - f(x_0) = \lambda\Delta x + o(\Delta x) \quad(\Delta x \rightarrow 0), $$ 则称函数$f$在点$x_0$处可微。函数的改变量的线性主要部分$\lambda \Delta x$称为$f$在$x_0$处的微分,记作$\text{d} f(x_0)$。
因此,当$|x - x_0|$相当小时有: $$ f(x) \approx f(x_0) + f'(x_0)(x - x_0) $$
一般地,关于函数四则运算的微分,有如下法则:
$\text{d} (f \pm g) = \text{d} f \pm \text{d} g$ $\text{d} (fg) = g \text{d} f + f \text{d} g$ -
$\text{d} (\frac{f}{g}) = \frac{g \text{d} f + f \text{d} g}{g^2}$ ,其中$g \neq 0$
导函数$f'$可以用$\frac{\text{d}f}{\text{d}g}$来表示,这是导数的Leibniz记号,因为$\frac{\text{d}f}{\text{d}g}$是函数的微分与自变量的微分的商,因此导数也称为微商。