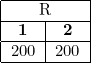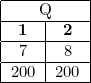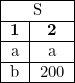'The chase' implementation

This contains implementations of some papers on the chase. I'll attempt to summarize the what and why of the chase below.

Background - relational algebra

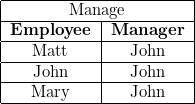
Connected with relational databases that you might be more familiar with is the concept of relational algebra. What we called tables are now called relations, which we can think of as sets of tuples of some fixed length. Importantly we can ask whether a given tuple 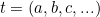is an element of a given relation 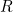, i.e. is it the case that 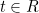$t \in R$ ? We can isolate particular attributes of a tuple by projection, which we could use subscripts for: e.g. if the previous tuple was 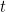, then 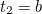. It's easiest to visualize the relations as tables:

$\begin{tabular}{ |c|c| } \hline \multicolumn{2}{ |c| }{Likes} \ \hline \textbf{Liker} & \textbf{Likee}\ \hline Matt & John \ \hline John & John \ \hline John & Mary \ \hline\end{tabular}$

$\begin{tabular}{ |c|c| } \hline \multicolumn{2}{ |c| }{Manage} \ \hline \textbf{Employee} & \textbf{Manager}\ \hline Matt & John \ \hline John & John \ \hline Mary & John \ \hline\end{tabular}$

We can use first-order logic to express constraints. We can express that "Employee is a primary key of Manage" by 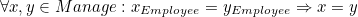$\forall x, y \in Manage: x_{Employee}=y_{Employee} \Rightarrow x=y$ . We can express that "Likee is a foreign key 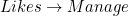$Likes \rightarrow Manage$ " by writing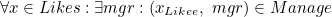 $\forall x \in Likes: \exists mgr: (x_{Likee},\ mgr) \in {Manage}$

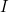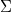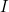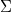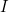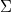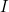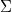Now suppose we have a database and a set constraints $\Sigma$ , we can ask whether satisfies $\Sigma$ . If not, we can imagine there being the best or nearest-relative of that does satisfy $\Sigma$ . The chase is an algorithm that finds this other database, given and $\Sigma$ . The remaining background material to cover concerns how to define this notion of a "best" relative of .

Background - database homomorphisms

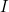One interesting relationship between databases is whether one is a subset of the other.

$\begin{tabular}{ |c|c| } \hline \multicolumn{2}{ |c| }{R} \ \hline \textbf{1} & \textbf{2}\ \hline 200 & 200 \ \hline\end{tabular}$

$\begin{tabular}{ |c|c| } \hline \multicolumn{2}{ |c| }{Q} \ \hline \textbf{1} & \textbf{2} \ \hline 7 & 8 \ \hline 200 & 200 \ \hline\end{tabular}$

We'll consider single-relation database instances in this section to keep the examples small, which allows us to abuse notation and treat the relations as databases in their own right. In the above examples, we could say 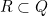$R \subset Q$ to mean one database is a subset of the other.

Although all example databases above have been fully specified, generally databases in this formalism can have "labeled nulls" which behave like variables.

$\begin{tabular}{ |c|c| } \hline \multicolumn{2}{ |c| }{S} \ \hline \textbf{1} & \textbf{2} \ \hline a & a \ \hline b & 200 \ \hline\end{tabular}$

This new instance 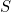says there's a tuple that has two of the same unknown value, and another which has an unknown first value and 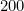for the second value. We need to refine our notion of 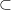$\subset$ in light of the possibility of labeled nulls. The relevant relation now is called a homomorphism ( 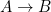$A \rightarrow B$ ) which consists in an assignment to the labeled nulls in 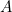such that, when substituting 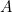with this assignment, we get a database instance that is literally a subset of 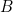. For example, the assignment 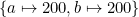${a \mapsto 200, b \mapsto 200}$ is a homomorphism 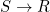$S \rightarrow R$ . There is no homomorphism 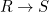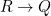$R \rightarrow S$ . ( $R \rightarrow Q$ is a homomorphism trivially, no substitution needed; for any 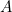we have 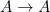$A \rightarrow A$ , given we can make an identity substitution).

Even with merely a simple binary relation like 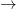$\rightarrow$ , we can derive a notion of the 'closest' related 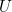for some given 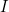. Fix a given 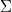$\Sigma$ of constraints and imagine the set of all possible instances which both satisfy 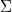$\Sigma$ and are related to 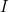. Among this set, it may be the case that there exists a 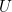such that 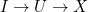$I \rightarrow U \rightarrow X$ for all 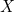instances in this set, i.e. any homomorphism can be factored through a homomorphism with .

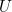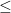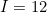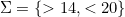(Analgously, consider the relation $\le$ for integers, let and $\Sigma = {> 14, < 20}$ ... we want something that is 'related' to 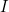, so we are looking for an 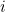such that 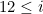$12 \le i$ which also satisfies the constraints. There exist 5 possible candidates ( 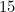through 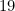inclusive) and it happens that for any candidate 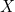we can write 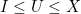$I \le U \le X$ with the value of 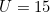. Thus, 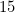is the 'closest' integer to 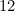that satisfies the constraints.)

The database instance 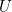that satisfies this property is called universal (with respect to 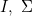$I,\ \Sigma$ ), and this is the instance that the chase returns, if it exists.

Why

Reading about what the chase is and how it works will be more interesting with context as to why finding a universal database instance is of interest.

Query Optimization
Constraint Implication
Universal Solutions / Data Exchange
Certain Answers

What

The simplest variation of the chase considers each constraint as a potential trigger which can be fired to produce a new instance that satisfies that constraint. We then iteratively repeat this process until there exist no active triggers (i.e. produce a sequence of instances until we arrive at one which satisfies the constraints).

The literature is generally concerned with two types of constraints.

Tuple-generating dependencies: if there exist some tuples satisfying such-and-such conditions, then there must exist these other tuples satisfying such-and-such conditions. To fire this constraint is to add the tuples in the consequent clause.
Equality-generating dependencies: if there exist some tuples (which involve two variables, say and 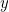) satisfying such-and-such conditions, then 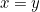. To fire this constraint is to take all instances of 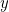and replace them with (or vice-versa). If both and 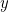match with constants which have different values, then the chase fails.
In both cases, there is a clear antecedent condition to check to see if the trigger is active.

It's possible for the sequence of instances generated by firing constraints to never terminate. For some simple chase implementations, this doesn't imply that a universal solution doesn't exist. However, more sophisticated implementations (such as the core chase) are complete, meaning they terminate iff there exists a solution.

Functionality

This repo has implementations in different languages.

Language	Python	Haskell
Run test suite	✅ Run `pytest test_chase.py`	✅ Run `stack test`
Read relations / database instances from CSV	✅	✅
Fire TGD and EGDs	✅	✅
Basic chase algorithm	✅	❌

References

Gösta Grahne and Adrian Onet. Anatomy of the Chase. Fundamenta Informaticae. 157 (2018) 221–270.
Alin Deustch, Alan Nash, and Jeff Remmel. The chase revisited. PODS (2008).

kris-brown / chase