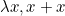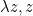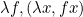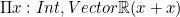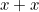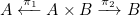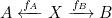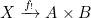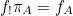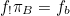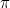calculus_of_constructions

Background: What is CoC

The CoC provides a language with which we can express mathematical terms (e.g. 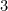, , 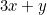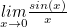$\underset{x \rightarrow 0}{lim}\frac{sin(x)}{x}$ ) and types (e.g. pairs of real numbers 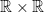$\mathbb{R} \times \mathbb{R}$ , the type of functions 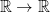$\mathbb{R} \rightarrow \mathbb{R}$ , the type of lists of length ).

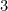The basic CoC syntax describes how to construct pseudoterms, which will represent types and terms.

Variables, e.g.
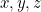
Applying a function to a term, e.g. f(x) (often written without parentheses, e.g. plus n m)
Lambda abstractions
- describe functions that substitute a variable into a body expression, e.g.:
  - the doubling function $\lambda x, x+x$
  - the identity function $\lambda z, z$
  - a function which takes two arguments and applies the first to the second: $\lambda f, (\lambda x, f x)$ .
Pi types
- represent the types of functions
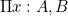- $\Pi x:A, B$ refers to the type of functions that take a term of type 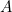and return a term of type 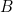(which may or may not depend on the value of the input, )).
  - E.g.:
    - Let vectors be sequences of a certain type with a fixed length
    - The term $\Pi x:Int, Vector \mathbb{R} (x+x)$ can be applied to an integer
    - This returns the type of lists of real numbers of length .
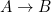- Often there's no dependence on the at all, so we abbreviate the notation of these cases as $A \rightarrow B$ .
- Given the meaning of 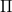$\Pi$ , it is often written as 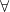$\forall$ (which means "for all").
The word sort refers to the type of a type. In the flavor of CoC we implement here, we have as axioms the existence of two 'ground level' sorts 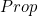and 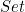, as well as an infinite sequence higher order sorts 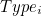for any natural number .

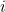The power of the CoC comes from a set of accompanying rules which allow us to construct terms of a certain type. This firstly allows us to show that a term is not nonsense, e.g. treating a natural number as a function: 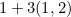. Furthermore, we can prove judgments saying a term has a certain type. Notationally we write this as 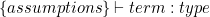${assumptions} \vdash term : type$ . These judgment-forming rules (described in the references below) capture the meanings of the symbols described above, so that we can prove things like:

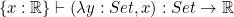
${x:\mathbb{R}} \vdash (\lambda y: Set, x) : Set \rightarrow \mathbb{R}$
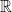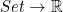i.e. a lambda expression which accepts a set but ignores it and returns a constant of type $\mathbb{R}$ has the type of $Set \rightarrow \mathbb{R}$ .

Why is it interesting

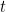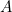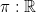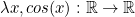If the only thing we can do is show that term has type , it may be confusing as to what's the interest in this language at all, since the fact that $\pi: \mathbb{R}$ or $\lambda x, cos(x): \mathbb{R} \rightarrow \mathbb{R}$ aren't that remarkable. What we care about are more elaborate propositions we can make about these mathematical terms, such as:

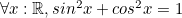
$\forall x: \mathbb{R}, sin^2x+cos^2x=1$
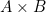
for the type of pairs of $A \times B$
- there exists a unique pair of projection functions $A \xleftarrow{\pi_1} A \times B \xrightarrow{\pi_2} B$ such that for any pair of functions $A \xleftarrow{f_A} X \xrightarrow{f_B} B$ , there is a unique map $X \xrightarrow{f_!} A\times B$ such that $f_!\pi_A = f_A$ and $f_!\pi_B=f_b$ (i.e. one can always factor out a $\pi$ component from the functions).
After encoding the relevant real-world entities into the CoC, we might want to prove certain compiler optimization does not alter the meaning of the unoptimized code, or that a critical piece of code has no bugs.

It turns out our simple typing judgments are capable of proving such kinds of elaborate mathematical statements, due to a remarkable correspondance (called the Curry Howard Isomorphism) between the above language and the language of logic. Logical operations such as and, or, for all, not, etc. each have analogues which behave just as they do in logic.

Other than learning the exact translations for each of these operations, the key insight is to think of propositions as types with terms as proofs of that proposition.
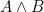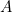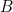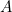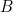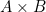The logical relation $A \land B$ ( and ) can be proved if and only if we have a proof of and a proof of , which is tantamount to having a term of the type of pairs $A \times B$ .
The logical relation 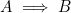$A \implies B$ (if 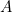, then 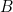) is tantamount to a function type 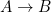$A \rightarrow B$ , which provides a proof of 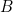if you feed it a proof of .

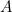Continuing in this fashion, we can construct arbitrarily complex statements about arbitrarily complex mathematical structures and have a computer mechanically verify them. Discovering these proof terms is not a step that can be fully automated, though this is a field of active research.

Inductive types

In this repo, we use some common extensions of CoC to make it more usable, most notably adding inductive types.

Although booleans, natural numbers, and other types can be defined (called the Church encoding) with the above infrastructure, inductive types allow for an efficient and intuitive representation. A term of an inductive type must be constructed by one of its custom constructors and eliminated by case analysis (e.g. a function I -> X for some inductive type I must be defined for all possible constructors of I). These are easiest explained through examples (which can be found in data/base.txt):

The type of Booleans, Bool, can be modeled as an inductive type - i.e. something that is either true or false.

Inductive Bool : Set :=
| tt : Bool
| ff : Bool.

The natural numbers are a prototypical example of inductive types, as any element of it is either zero or the successor to another natural number (thus, zero lets us construct a Nat in any context, and the succ constructor behaves like a function of type Nat → Nat).

Inductive Nat : Set :=
| zero : Nat
| succ : Nat → Nat.

Lists and vectors force us to consider inductive types that have a parameter, i.e. List itself isn't a type but rather must be applied to some parameter (in this case, A, an arbitrary Type) to form a type. All of the constructors implicitly require this parameter too, in addition to other arguments (nil B lets us construct an empty List B, while an element c:C can be added to a list l_c:List C by calling cons C c l_c which produces another element of type List C).

Inductive List (A: Type) : Type :=
| nil : List A
| cons : A → List A → List A.

Vectors work very similarly, but keep track of how long the length of the list is at the type level (the Vnil X case is forced to be of type vector X 0 rather than any other number, and Vcons will always increment the type-level counter each time an element is appended).

Inductive vector (A: Type) : (Nat → Type) :=
| Vnil : vector A zero
| Vcons : A → vector A n → vector A (succ n).

We now introduce the basics of "propositions as types" (which are distinct from the encoding of true and false as values of type Bool). We model the proposition True (AKA ⊤/Unit/()) as an inductive type with a single constructor. In any context we are justified in producing a term of this type, reflecting how trivial it is to 'prove' True.

Inductive True : Prop :=
| true_mk : True.

We model False (⟂/Void) as an inductive type with no constructors. It is not possible to construct a term of this type (i.e. prove False) without being in a trivial context that can prove anything (this allows us to model Not A as A -> False, meaning A is absurd enough to prove anything).

Inductive False : Prop :=.

There are two constructors for Or A B to reflect either a proof of A or a proof of B is sufficient to prove the disjunction, while And A B works as described above.

Inductive OR (A: Prop) (B: Prop) : Prop :=
| inl : A → OR A B
| inr : B → OR A B.

Inductive AND (A: Prop) (B: Prop) : Prop :=
| and_mk : A → B → AND A B.

As a final example, consider the proposition that p ≤ q. If less-than-or-equal-to (le) is defined as below, then we know it could have only been constructed from one of two scenarios:

p = 0, in which case it's true because 0 is less than or equal to every natural number
p-1 ≤ q-1, i.e. we have a proof that after peeling back one successor from each number that the property holds (we can keep doing this and reach zero eventually if and only if truely p ≤ q).

Inductive le: (Nat → Nat → Prop) :=
| le_n : ∀ (n: Nat), le zero n
| le_S : ∀ (n: Nat) (m: Nat), le n m -> le (succ n) (succ m).

In fact, knowing that these are the only two constructors allows us to prove that it's not the case that 1 ≤ 0.

Functionality

This repo has implementations in different languages.

Language	Python	Haskell
Run test suite	✅ Run `pytest test.py`	✅ Run `stack test`
Judge/typecheck pseudoterms to determine types	✅	✅
Evaluate/β-reduce expressions	✅	✅
Pretty print and parse files of expressions	✅	✅
Property tests	❌	❌
Well-formedness/termination checking of terms	❌	❌

References

TODO

kris-brown / calculus_of_constructions