PyDualNumber

This project provides a basic implementation of dual numbers in Python with an example application of dual numbers for automatic differentiation. Possibly interesting for educational purposes.

Dual Numbers

The dual numbers system was introduced 1873 by the English mathematician William Clifford.

Dual numbers are of the form $x = a + b \epsilon$, where $a$ and $b$ are real numbers, and $\epsilon$ for which the property $\epsilon^2 = 0$ holds.

Arithmetic Operations

The arithmetic operations for dual numbers are defined as follows.

Operation
Addition	$$(a + b \epsilon) + (c + d \epsilon) = (a + c) + (b + d) \epsilon$$
Subtraction	$$(a + b \epsilon) - (c + d \epsilon) = (a - c) + (b - d) \epsilon$$
Multiplication	$$(a + b \epsilon) (c + d \epsilon) = a c + (a d + b c) \epsilon$$
Division	$$\frac{a + b \epsilon}{c + d \epsilon} = \frac{a}{c} + \frac{b c - a d}{c^2} \epsilon$$

Differentiation

Any real function can be extended to the dual numbers.To see this, we can employ the Taylor series given by:

$$f(x) = \sum_{k=0}^{\infty}\frac{f^{(k)}(x_0)}{k!}(x-x_0)^k$$

We are interested in the behavior of a real function extendend by dual numbers. Therefore, we set $x=x_0+b\epsilon$ with $x_0=a$.

$$f(x) = \sum_{k=0}^{\infty}\frac{f^{(k)}(a)}{k!}(b\epsilon)^k$$

By the definition of $\epsilon$, all terms with $k>1$ disappear. Thus, we end up with

$$f(a+b\epsilon) = f(a) + f'(a)b\epsilon$$

This property is especially interesting for automatic differentiation.

We can use this expression to extend functions such as hyperbolic or power functions to the dual numbers.

$f(x)$	$f(a+b\epsilon)$
$\sin(x)$	$\sin(a) + \cos(a)b\epsilon$
$\cos(x)$	$\cos(a) - \sin(a)b\epsilon$
$\tanh(x)$	$\tanh(a) + (1 - \tanh(a)^ 2)b\epsilon$
$\exp(x)$	$\exp(a) + \exp(a)b\epsilon$
$\ln(x)$	$\ln(a) + \frac{1}{a}b\epsilon$

Rectified Liner Unit Activation Function (ReLU)

We can also extend activation functions such as $\text{ReLU}(x)$ for dual numbers. The definition for the $\text{ReLU}$ activation functions is given by

$$ \text{ReLU}(x) = \begin{cases} x & x > 0\\ 0 & \text{else} \end{cases} $$

and thus it follows for dual numbers

$$ \text{ReLU}(a+b\epsilon) = \begin{cases} a + 1b\epsilon & x > 0\\ 0 & \text{else} \end{cases} $$

Exponentiation

We ca use the expressoin $f(a+b\epsilon) = f(a) + f'(a)b\epsilon$ also for slightly more complex expresssions such as $f(x, y) = x^y$ where both $x$ and $y$ are dual numbers.

For this to work we use the Taylor series for two variables up to the first order:

$$f(x, y) = f(x_0, y_0) + \partial_x f(x_0, y_0)(x-x_0) + \partial_y f(x_0, y_0)(y-y_0) + \cdots$$

Again we won't consider higher order terms as these become zero since $\epsilon^2 = 0$. Applying the same logic as above using $x=a+b\epsilon$ and $y=c+d\epsilon$ with $x_0=a$ and $y_0=c$ we derive an expression for the extension of a function of two variables for dual numbers:

$$f(a+b\epsilon, c+d\epsilon) = f(a, c) + \partial_x f(a, c)b\epsilon + \partial_y f(a, c)d\epsilon$$

Now we have everything to extend $f(x, y) = x^y$ to dual numbers:

$$f(a+b\epsilon, c+d\epsilon) = a^c + (ca^{c-1}b + a^c\ln(a)d)\epsilon \ = a^c + a^c(\frac{b}{a}c + \ln(a)d)\epsilon$$

Thus, for the actual implementation in Python, the following cases for exponentiation involving dual numbers are of interest.

$f(x, y)$	$f(a+b\epsilon, c+d\epsilon)$
$x^y$	$a^c + a^c(\frac{b}{a}c + \ln(a)d)\epsilon$
$x^c$	$a^c + a^{c-1}bc\epsilon$
$a^y$	$a^c + a^c\ln(a)d\epsilon$

As you can see, this expression can also be used to compute quantities where $x$ or $y$ are just real numbers.

Examples

Example usage

from dualnumber import Dual

d1 = Dual(1, 2)
d2 = Dual(3, 4)
d3 = d1 + d2
d4 = d3 - d2
d5 = d4 * d3
d6 = d5 / d4
d7 = d6.sin()
d8 = d7.cos()
d9 = d9.tanh()
d10 = d9.ln()
d11 = d10.exp()
d12 = d11**d10
d12 = d11.relu()

Automatic Differentiation with Dual Numbers

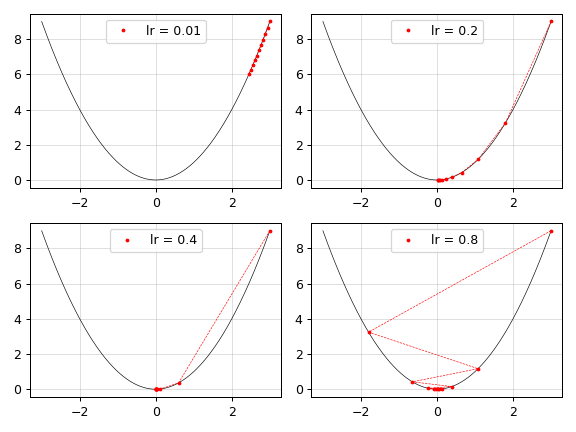
Dual numbers are great for automatic differentiation. Here is a toy example showing gradient descent for $f(x)=x^2$ and different step sizes with dual numbers.

Run the example

cd PyDualNumber
python -m examples.gradient_descent

Installation

Run the following command to install this package in your environment:

cd PyDualNumber
pip install .

Install required packages to run the example, tests, and to facilitate development according to clean code principles:

cd PyDualNumber
pip install -r requirements.txt

Tests

Run the tests by executing:

cd PyDualNumber
pytest dual_number

Clean Code

Some good practices for software developement in Python.

Checking type consistency

Install static type checker mypy:

pip install mypy

Ignore false positives by adding a marker as a comment:

a = "bla"   # type: ignore

Check type consistency by running:

mypy dual_number

Checking Code Structure

Install pylint to check for generic code structure:

pip install pylint

Check code structure by running:

pylint dual_number

Or run pylint with a customiced pylintrc file:

pylint --rcfile dual_number/pylintrc dual_number

Automatic Formatting

This project uses flake8 and black for automatic formatting.

Install flake8 for full flexibility and configurability and black for uncompromising and deterministic code formatting:

pip install flake8
pip install black

Run tools for automatic formatting:

flake8 dual_number
black --check dual_number

Remove the --check flag to perform automatic formatting changes.

Automatic Checks

Instead of running all checks manually we can make use of Makefiles to run them all automatically. Run the following command in the root folder:

cd dual_number
make check

This check will automatically fail if at least one check fails. To run all checks ignoring errors by running:

cd dual_number
make --ignore-errors check  # or: make -i check

Citation

If you find this content useful, please cite the following:

@misc{KaiFischer2022pdn,
  author = {Fischer, Kai},
  title = {PyDualNumber},
  year = {2022},
  publisher = {GitHub},
  journal = {GitHub repository},
  howpublished = {\url{https://github.com/kaifishr/PyDualNumber}},
}

Licence

MIT

kaifishr / PyDualNumber