A basic implementation of a Perceptron, the building block of a Neural Network
A Multilayer Perceptron is a connected collection of individual Perceptrons capable of solving more advanced problems than a single Perceptron. They are organized by layers, each feeding their output as an input into each perceptron in the next layer.
Each Perceptron is considered a Neuron and this structure is considered as a Neural Network.
A Perceptron is limited in what it can solve. They can only solve "linearly separable" problems, meaning the classification between our answers can be divided with a single line.
Consider the problem of identifying a number within a picture. We would want our Perceptron to have an input for each pixel of the image, in a 20x20 image that would be 400 inputs. We need the Perceptron to give us a probability of what digit it is, one probability per digit. So we would have 10 outputs.
If we look at boolean OR and boolean AND and we create a table for them, we can see that both OR and AND can be linearly separable and therefore solved by our Perceptron.
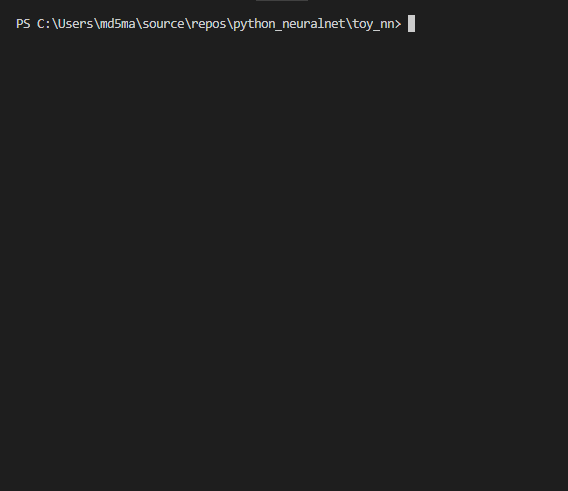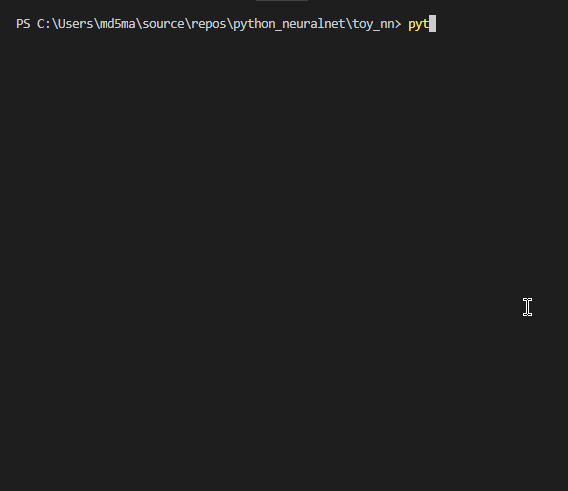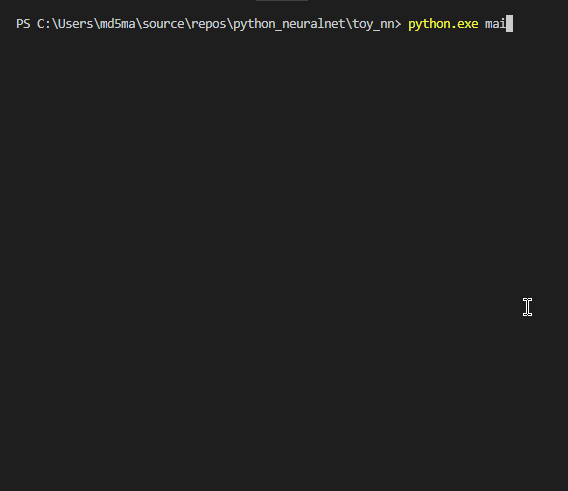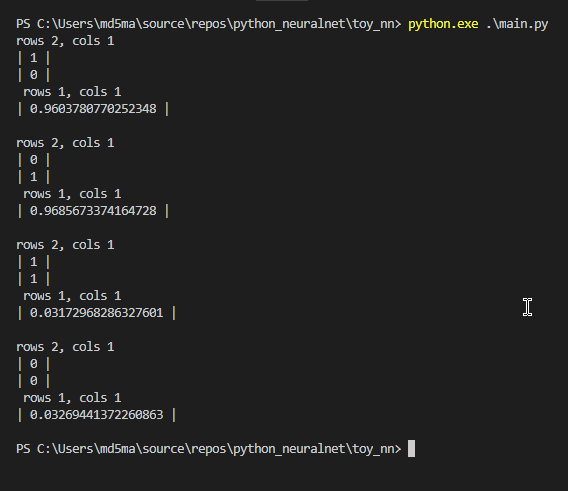
However for XOR boolean operations we cannot linearly separate them and therefore XOR cannot be solved by a single Perceptron.
If we break down what XOR is, we can see it it is the combination of AND and OR: XOR = !AND && OR. Therefore we could train one perceptron on !AND, another on OR and feed their inputs to a third trained on AND. These connected Perceptrons would produce a correct XOR answer.
To generalize a Neural Network in code, we want to create: an input layer with a number of input neurons, a hidden layer with a number of hidden neurons, and an output layer with the number of output neurons.
Example: new NeuralNetwork(input=2, hidden=3, output=2);
In a Fully Connected network every preceding layer's neurons are connected to every successive neighboring layer's neurons. So with 2 input neurons, each one sends its outputs to every hidden neuron so in total there are 6 connections. Then each hidden neuron sends its output to each output neuron.
More advanced Neural Networks have several hidden layers, not just one, in order to process more complicated problems.
In a Feed Forward network each neuron will do a weighted sum of the incoming data and weights. So for our 2/3/2 NN a single hidden neuron will have two connections of data coming in as inputs. Each connection has its value and its weight and it will multiply each value times its weight and add them to each other input's. sum = x1 * w1 + x2 * w2 + ... xN * wN. See the Perceptron doc for more detail.
Once the weighted sum is calculated in the neuron, it is passed through the "activation function" (see perceptron.md) and the output is passed on to the next layer as inputs.
An obvious approach to modeling this structure would be to model each neuron as an object and each connection to the neuron as another object. At that stage you could pass data forward through neurons doing calculations one by one. But the standard approach to modeling the data as it passes through a network is to use a Matrix.
A simpler example we can break down:
NN (2 inputs, 2 hidden, 1 output)
If x1 is fed into the first input, and x2 is fed into the second input, and its a fully connected feed forward network then we can use linear algebra to calculate the sums of the hidden layer.
w11
x1 -> ( i1 )---( h1 )
\/w12 \
/\ >--( o1 )
/ \w21 /
x2 -> ( i2 )---( h2 )
w22
Weights:
- w1-1 is the weight from input 1 to hidden 1
- w1-2 is the weight from input 1 to hidden 2
- w2-1 is the weight from input 2 to hidden 1
- w2-2 is the weight from input 2 to hidden 2
Matrix Notation:
(w11 w21) * (x1) = (h1)
(w12 w22) (x2) (h2)
We have a 2x2 matrix of weights and a 2x1 matrix of inputs (rows by cols).
We need a weighted sum as seen with our perceptron. h1 sum = x1 * w11 + x2 * w21 and h2 sum = x1 * w12 + x2 * w22.
These summations are linear algrebra of matrix multiplication.
See the neural network linear algreba doc on matrix mathematics used to calculate our weighted sums through a dot product.
With our understanding of a Perceptron and a Multilayer Perceptron structure, we understand that each neuron will calculate the weighted sum of its inputs and their connected weights.
What we can use is matrix mathematics to perform this math for us to multiply a weight matrix by the input matrix to recieve the sums of our neurons (before the activation function).
An example with 3 input neurons, 2 hidden neurons and 1 output neuron:
- There are 3 Input neurons: x1, x2, x3
- There are 2 Hidden neurons: h1, h2
We want to organize our weights by their hidden neuron and their input neuron.
- There are 6 weights: w11 for h1-x1, w12 for h1-x2, w13 for h1-x3, w21 for h2-x1, w22 for h2-x2, w23 for h2-x3
If we model the weights of our neurons as a matrix we should see:
W = [ w11 w12 w13 ] 2x3 matrix
[ w21 w22 w23 ]
Then we want to model our input neurons with a matrix, one row per input:
X = [ x1 ] 3x1 matrix
[ x2 ]
[ x3 ]
We can take the Dot Product of these two matrices because the columns in the weight matrix are the same as the number of rows in the input matrix.
NOTE we organize the weights by hidden-to-input and then create the input matrix second because thats the only way to get the matrices to be a 2x3 dot 3x1.
dot product of weights
W . X = H
[ w11 * x1 + w12 * x2 + w13 * x3 ] = [ h1 ]
[ w21 * x1 + w22 * x2 + w23 * x3 ] = [ h2 ]
In our Perceptron model we recognized the limitation of dealing with 0 value inputs because the weights would always calculate as 0. To overcome this we introduced a bias that was added against the weighted sum to always prevent a zero summation.
If H = W . X (hidden values equal weight matrix dot product the input matrix), we need to add our bias into that. That becomes H = W . X + B where B is the bias matrix.
We would have one bias value per hidden neuron so:
B = [ b1 ] 1x2
[ b2 ]
and
W . X = S
S + B = H
dot prduct
[ w11 * x1 + w12 * x2 + w13 * x3 ] = [ s1 ]
[ w21 * x1 + w22 * x2 + w23 * x3 ] [ s2 ]
element-wise addition
[ s1 ] + [ b1 ] = [ h1 ]
[ s2 ] [ b2 ] [ h2 ]
[ s1 + b1 ] = [ h1 ]
[ s2 + b2 ] [ h2 ]
The Sigmoid Function is a function that has the characteristic of an "S" or sigmoid curve. On a cartesian coordinate the lower left of the S would start at about -6,0, the center point would be 0,0.5 and the upper right would be at about 6,1. We can see that the x range is hyperbolically between -6 and +6 and the y from 0 to 1.
S(x) = f(x) = 1 / (1 + e^-x)
It is used in neural networks because if you pass any number into the sigmoid function you will get a number between 0 and 1.
Using the sigmoid function as an activation function our final hidden output calculation becomes the weight matrix dot input matrix plus bias matrix passed through the sigmoid function.
H = Sigmoid( W . X + B )
Now that we have the hidden layer outputs calculated, those outputs become the inputs for the final output neuron. The same feed forward algorithm is applied.
- Create our weighted matrix from output neuron mapped to input value
- Create our input matrix, each input per row
- Create our bias matrix, a bias per output neuron (1)
- Calculate the dot product and element-wise addition of these matrices
- Pass the result through the sigmoid function