A library of routines used for the analysis of dynamic systems.
This example illustrates how to compute the frequency response of Duffing's equation by sweeping across frequency.
program example
use iso_fortran_env
use dynamics
use fplot_core
use duffing_ode_container
implicit none
! Parameters
real(real64), parameter :: f1 = 0.5d0
real(real64), parameter :: f2 = 2.0d0
integer(int32), parameter :: nfreq = 100
integer(int32), parameter :: npts = 1000
real(real64), parameter :: pi = 2.0d0 * acos(0.0d0)
real(real64), parameter :: zmax = 1.0d1
real(real64), parameter :: zmin = 0.5d0
! Local Variables
type(duffing_container) :: sys
integer(int32) :: i
real(real64) :: dz, phase1(nfreq), phase2(nfreq), z(npts), w1(npts), w2(npts)
type(frf) :: solup, soldown
! Plot Variables
type(multiplot) :: plt
type(plot_2d) :: plt1, plt2
type(plot_data_2d) :: pd1, pd2, pd3, pd4
class(plot_axis), pointer :: xAxis, yAxis
class(legend), pointer :: lgnd
! Perform the ascending sweep
solup = sys%frequency_sweep(nfreq, f1, f2, [0.0d0, 0.0d0])
phase1 = atan2(aimag(solup%responses(:,1)), real(solup%responses(:,1)))
! Perform the descending sweep
soldown = sys%frequency_sweep(nfreq, f2, f1, [0.0d0, 0.0d0])
phase2 = atan2(aimag(soldown%responses(:,1)), real(soldown%responses(:,1)))
! Compute the analytical solution
dz = (zmax - zmin) / (npts - 1.0d0)
z = (/ (dz * i + zmin, i = 0, npts - 1) /)
w1 = sys%leg1(z)
w2 = sys%leg2(z)
! Plot the results
call plt%initialize(2, 1)
call plt1%initialize()
xAxis => plt1%get_x_axis()
yAxis => plt1%get_y_axis()
lgnd => plt1%get_legend()
call xAxis%set_title("{/Symbol w}")
call yAxis%set_title("X({/Symbol w})")
call lgnd%set_is_visible(.true.)
call lgnd%set_horizontal_position(LEGEND_LEFT)
call xAxis%set_autoscale(.false.)
call xAxis%set_limits(0.0d0, 2.0d0)
call pd1%define_data(solup%frequency, abs(solup%responses(:,1)))
call pd1%set_name("Ascending")
call pd1%set_draw_markers(.true.)
call pd1%set_marker_style(MARKER_EMPTY_CIRCLE)
call pd1%set_line_style(LINE_DOTTED)
call plt1%push(pd1)
call pd2%define_data(soldown%frequency, abs(soldown%responses(:,1)))
call pd2%set_name("Descending")
call pd2%set_draw_markers(.true.)
call pd2%set_marker_style(MARKER_EMPTY_SQUARE)
call pd2%set_line_style(LINE_DOTTED)
call plt1%push(pd2)
call pd3%define_data(w1, z)
call pd3%set_name("Analytical")
call pd3%set_line_color(CLR_BLACK)
call pd3%set_line_width(2.0)
call plt1%push(pd3)
call pd4%define_data(w2, z)
call pd4%set_line_color(CLR_BLACK)
call pd4%set_line_width(2.0)
call plt1%push(pd4)
call plt2%initialize()
xAxis => plt2%get_x_axis()
yAxis => plt2%get_y_axis()
call xAxis%set_title("{/Symbol w}")
call yAxis%set_title("{/Symbol f}({/Symbol w})")
call xAxis%set_autoscale(.false.)
call xAxis%set_limits(0.0d0, 2.0d0)
call pd1%define_data(solup%frequency, phase1)
call plt2%push(pd1)
call pd2%define_data(soldown%frequency, phase2)
call plt2%push(pd2)
call plt%set(1, 1, plt1)
call plt%set(2, 1, plt2)
call plt%draw()
end programTo compute the solution, a new type must be defined as a container for the ODE. This container type allows the frequency sweep solver to interact with the ODE and alter the excitation frequency. The following module illustrates this concept. Notice, the following module also contains routines for computing the analytical solution. The analytical solution routines are not necessary and are provided here simply for the example and comparison to the numerical solution.
module duffing_ode_container
use iso_fortran_env
use dynamics
implicit none
type, extends(harmonic_ode_container) :: duffing_container
! Duffing Model Parameters
real(real64) :: alpha = 1.0d0
real(real64) :: beta = 4.0d-2
real(real64) :: delta = 1.0d-1
real(real64) :: gamma = 1.0d0
contains
procedure, public :: ode => duffing_ode
! The following procedures are not necessary for an actual
! implementation. They are being used for comparison for the purposes
! of the example.
procedure, public :: leg1
procedure, public :: leg2
end type
contains
subroutine duffing_ode(this, x, y, dydx)
! The overload of the base ODE routine.
class(duffing_container), intent(in) :: this
real(real64), intent(in) :: x
! The independent variable.
real(real64), intent(in), dimension(:) :: y
! An array of the N dependent variables.
real(real64), intent(out), dimension(:) :: dydx
! An output array of length N where the derivatives are written.
! Variables
real(real64) :: f
! Compute the harmonic forcing function
! - note the use of excitation_frequency
f = this%gamma * sin(this%excitation_frequency * x)
! Compute the derivatives
dydx(1) = y(2)
dydx(2) = f - this%delta * y(2) - &
this%alpha * y(1) - this%beta * y(1)**3
end subroutine
! Analytical Solution - Not necessary for the analysis, but used for
! the purpose of comparison.
pure elemental function leg1(this, z) result(rst)
use ieee_arithmetic
class(duffing_container), intent(in) :: this
real(real64), intent(in) :: z
real(real64) :: rst
! Local Variables
real(real64) :: arg, s, nan
! Process
nan = ieee_value(nan, ieee_quiet_nan)
arg = 4.0d0 * this%gamma**2 - 3.0d0 * this%beta * this%delta**2 * &
z**4 + (this%delta**2 - 4.0d0 * this%alpha) * this%delta**2 * z**2
if (arg < 0.0d0) then
s = -1.0d0
else
s = (2.0d0 * sqrt(arg) + z * (3.0d0 * this%beta * z**2 - &
2.0d0 * this%delta**2 + 4.0d0 * this%alpha)) / (4.0d0 * z)
end if
if (s < 0.0d0) then
rst = nan
else
rst = sqrt(s)
end if
end function
pure elemental function leg2(this, z) result(rst)
use ieee_arithmetic
class(duffing_container), intent(in) :: this
real(real64), intent(in) :: z
real(real64) :: rst
! Local Variables
real(real64) :: arg, s, nan
! Process
nan = ieee_value(nan, ieee_quiet_nan)
arg = 4.0d0 * this%gamma**2 - 3.0d0 * this%beta * this%delta**2 * &
z**4 + (this%delta**2 - 4.0d0 * this%alpha) * this%delta**2 * z**2
if (arg < 0.0d0) then
s = -1.0d0
else
s = (-2.0d0 * sqrt(arg) + z * (3.0d0 * this%beta * z**2 - &
2.0d0 * this%delta**2 + 4.0d0 * this%alpha)) / (4.0d0 * z)
end if
if (s < 0.0d0) then
rst = nan
else
rst = sqrt(s)
end if
end function
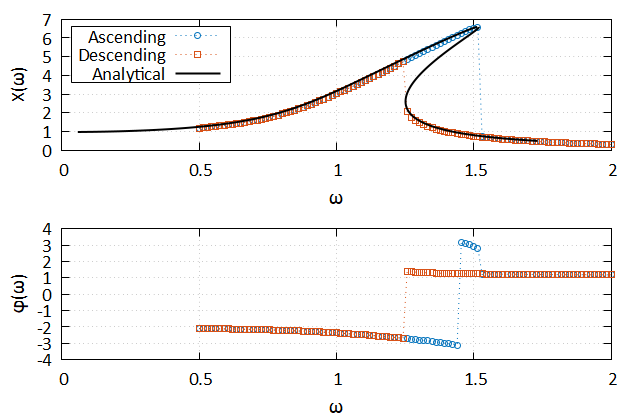
end moduleUsing the fplot library, this example produces the following plot.
- J. D. Hartog, "Mechanical Vibrations," New York: Dover Publications, Inc., 1985.
- S. S. Rau, "Mechanical Vibrations," 3rd ed., Reading, MA: Addison-Wesley Publishing Co., 1995.
- R. N. Jazar, "Advanced Vibrations," 2nd ed., New York: Springer, 2022.
- W. T. Thomson, "Theory of Vibration with Applications," 4th ed., New York: Springer, 1993.
- A. H. Nayfeh and B. Balachandran, "Applied Nonlinear Dynamics. Analytical, Computational, and Experimental Methods," New York: John WIley & Sons, Inc., 1995.
- L. Meirovitch, "Fundamentals of Vibrations," Long Grove, IL: Waveland Press, Inc., 2001.