j127 / 3drenderer

3drenderer

Learning about 3D graphics and C.

Dependencies

This installs GCC and the C dependencies along with SDL2.

$ sudo apt install build-essential
$ sudo apt install libsdl2-dev

Structure

Sample structure:

3drenderer
├── Makefile
└── src
    ├── main.c
    ├── mesh.c
    └── mesh.h

Compiling

The most simple:

$ gcc main.c -o renderer
$ ./renderer

See the Makefile.

Examples

Scalars

• temperature
• area
• length
• pressure

Vectors

• velocity
• acceleration
• force
• lift
• drag
• displacement

A cube will be a set of vectors represented by points (originating at 0, 0, 0).

2D vector: (6.0, 3.0) -- two components 3D vector: (3.0, 2.0, 3.0) -- three components

// Creating a new data type for 2D vectors
typedef struct {
    float x;
    float y;
} vec2_t; // _t here is a convention for naming the type

vec2_t p0 = { 0.0, 2.0 };
vec2_t p1 = { 3.0, 2.0 };
vec2_t p2 = { 4.5, -2.2 };

// 3D vector
typedef struct {
    float x;
    float y;
    float z;
} vec3_t;

// etc.

Example camera:

typedef struct {
    vec3_t position;
    vec3_t rotation;
    vec3_t fov_angle;
} camera_t;

camera_t mycam = {
    { 0, 0, 0 },
    { 0.3, -2.0, 0.0 },
    0.78
};

Projection

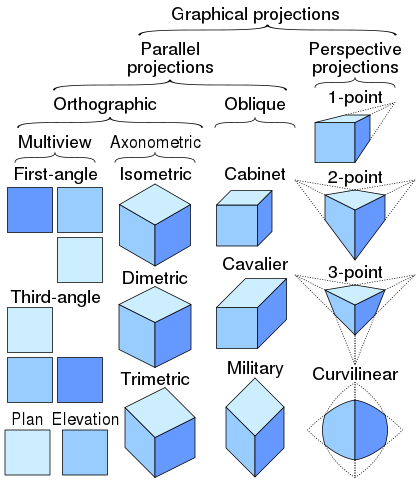
Two main categories: parallel and perspective.

Some branches of the tree:

• Parallel → Orthographic (→ Axonometric → Isometric)
• Perspective -- uses a view frustum (the clipped pyramid of vision).

Graphical projections image used under CC licence from here.

Isometric Projection

True isometric projection has 120 degree angles between x, y, and z. Most "isometric" games use 126.87 degrees to make a 2:1 pixel ratio.

Perspective Divide

Two similar triangles ABC (between eye and 2D viweing plane or screen) and ADE (between eye and 3D object):

BC   AB
-- = --
DE   AD

In his diagram, P'x is the width of the object on the screen (viewed from above), Px is the real width of the 3D object, and Pz is the real distance to the 3D object.

P'x   1
--- = --
Px    Pz

so, the width of the object on the screen (P'x) is the real width of the 3D object (Px) over the distance to the 3D object (Pz):

      Px
P'x = --
      Pz

The farther away the object is, the greater the denominator and the smaller P'x will be.

It's the same calculation for y:

P'y   1
--- = --
Py    Pz

      Py
P'y = --
      Pz

Coordinate System Handedness

We're using a left-handed coordinate system here (z increases as you go deeper into the monitor). DirectX uses a left-handed coordinate system. OpenGL uses a right-handed coordinate system.

Transformations

Frame-by-frame steps:

1. process_input(void)
2. update(void)
   • transform_points():
     • rotate(x, y, z)
     • scale(amount)
     • translate(amount) (move objects around by x, y, z)
   • project_points(perspective)
3. render(void)
   • draw_projected_points()

Trigonometric Functions

Angle α:

sin(α)=o/h
cos(α)=a/h
tan(α)=o/a

Rotation Matrix

┌             ┐   ┌   ┐
│cos α -sin α │   │ x │
│             │ * │   │
│sin α  cos α │   │ y │
└             ┘   └   ┘

2D Vector Rotation

The right triangle that a vector's ((x, y)) angle α makes with x as its adjacent side can be rotated by angle β. The hypotenuse of that triangle can be called r because it forms the radius of a circle as the vector rotates.

So the length of the adjacent side of the triangle is x and the length of the opposite side is y.

For the original vector:

• cos(α)=x/r -- so x=r*cos(α)
• sin(α)=y/r -- so y=r*sin(α)

If you rotate the angle of the vector by β, the new vector's angle will be α+β. The length of the hypotenuse remains the same (r, representing the rotation circle's radius).

That gives us cos(α+β)=x'/r and sin(α+β)=y'/r, and we know all the values except for x' and y':

• x'=r*cos(α+β)
• y'=r*sin(α+β)

or using angle addition formula for cosine:

x'=r(cosα cosβ - sinα sinβ)

which is:

r cosα cosβ - r sinα sinβ

and since we already know that r cosα = x and r sinα = y, we get the final formula that is found in rotation matrices:

x'=x cosβ - y sinβ

It's similar for y'. We started with:

• y'=r*sin(α+β)

Use the angle addition formula for sine:

y'=r(sinα cosβ + cosα sinβ)

which is:

y'=r sinα cosβ + r cosα sinβ

and since we already know that r sinα = y and r cosα = x, we get:

y'=y cosβ + x sinβ

Those will come up again later in rotation matrices:

┌             ┐   ┌   ┐
│cos α -sin α │   │ x │
│             │ * │   │
│sin α  cos α │   │ y │
└             ┘   └   ┘

3D Vector Rotation

• To rotate around x, x gets locked and everything rotates around x
• To rotate around y, y gets locked and everything rotates around y
• To rotate around z, z gets locked and everything rotates around z

Example:

To rotate around y:

• x'=x cosβ - z sinβ
• y'=y (no change)
• z'=x sinβ + z cosβ

vec3_t vec3_rotate_y(vec3_t v, float angle) { // angle is β
    vec3_t rotated_vector = {
        .x = v.x * cos(angle) - v.z * sin(angle),
        .y = v.y,
        .z = v.x * sin(angle) + v.z * cos(angle)
    };
    return rotated_vector;
}

Lines

y is slope times x plus y-intercept:

y=mx+c

Rise/run:

    Δy
m = --
    Δx

which is:

tan(α)= opposite/adjacent

If Δy/Δy=1, it's 45 degress. A descending line is <0.

Two Algorithms

• Digital Differential Analyzer (DDA) -- the code uses this algorithm.
• Bresenham -- division is a slow operation, so this avoids it (?)

Backface Culling

Pythagorean theorem: $h^2=o^2+a^2$

So the magnitude of the vector (hypotenuse) is the square root of the squares of adjacent and opposite sides.

       __________________
‖v‖ = ✓ (v.x)^2 + (v.y)^2

Vector Calculations

Addition

To visualize adding vectors a and b, move b to the end of a, and measure the length from the original origin to the tip of b. So just add the xs and add the ys.

Subtraction

To visualize vector subtraction, invert vector b (point in opposite direction) and then add the vectors (a + -b).

Multiplication and Division

By a scalar (see the code).

Vector Cross Product

Produces another vector that is perpendicular to both a and b.

a⨯b and b⨯a go in different directions.

The normal.

// example
vec3_t cross_product(vec3_t a, vec3_t b) {
    vec3_t result = {
        .x = a.y * b.z - a.z * b.y,
        .y = a.z * b.x - a.x * b.z,
        .z = a.x * b.y - a.y * b.x
    };
    return result;
}

The magnitude of the cross product relates to the area of the parallelogram. When a and b are exactly the same, the cross product is zero.

The magnitude of the cross product is the magnitude of a times the magnitude of b times the sine of the angle (θ) between a and b:

‖a⨯b‖ = ‖a‖ ‖b‖ sinθ

To get the normal: (a - b) ⨯ (a - c)

Dot Product

a·b is the projection of b onto a.

You can think of it as how aligned the vectors are. If they are the same, then the dot product will be 1.0. If they are perpendicular, the dot product will be 0.0. If the vectors start pointing away from each other, the dot product will be negative.

a·b = a_x b_x + a_y b_y

Culling Algorithm

The cross product shows where the face is pointing. The dot product shows whether the face is aligned with the camera.

(Not perfect, but the backfaces are removed.)

Normalizing Vectors

When you don't need to know the magnitude of a vector, you can normalize it by turning it into a unit vector (length=1).

(The as on the right side should have arrows on top, but I don't know the unicode character for that.)

     a
â = ---
    ‖a‖

Filling Triangles

Scanline fill -- scan each line from the top the to bottom and draw lines to fill the triangle.

Flat-top + flat-bottom technique.

          (x0, y0)
             /\
            /  \
           /    \
          /      \
         /        \
    (x1,y1)------(Mx,My)
        \_          \
           \_        \
              \_      \
                 \_    \
                   \    \
                     \_  \
                        \_\
                           \
                        (x2,y2)

By "top-to-bottom" it means that first they should be sorted by y values: y0 < y1 < y2.

The triangle is then split along the y-axis at (x1, y1) which crosses on the right side at a point (Mx,My). (He uses "M" for "midpoint".)

Use the ratio of similar triangles:

Mx - x0   y1 - y0
------- = -------
x2 - x0   y2 - y0

or:

(Mx - x0)(y2 - y0) = (x2 - x0)(y1 - y0)

Gives the formula:

     (x2 - x0)(y1 - y0)
Mx = ------------------ + x0
          (y2 - y0)