      88         oooo    oooo             .oooooo.                               88
    .8'`8.       `888   .8P'             d8P'  `Y8b                            .8'`8.
   .8'  `8.       888  d8'     .ooooo.  888      888 oo.ooooo.   .oooo.o      .8'  `8.
  .8'    `8.      88888[      d88' `88b 888      888  888' `88b d88(  "8     .8'    `8.
 .8'      `8.     888`88b.    888ooo888 888      888  888   888 `"Y88b.     .8'      `8.
.8'        `8.    888  `88b.  888    .o `88b    d88'  888   888 o.  )88b   .8'        `8.
88oooooooooo88   o888o  o888o `Y8bod8P'  `Y8bood8P'   888bod8P' 8""888P'   88oooooooooo88
                                                       888
                                                      o888o

What is KeOps?

KeOps is a cpp/cuda library that comes with bindings in python (numpy and pytorch), Matlab or R (coming soon). KeOps computes efficiently Kernel dot products, their derivatives and other similar operations on the GPU. It provides good performances and linear (instead of quadratic) memory footprint through a minimal interface.

In short: KErnel OPerationS, on CPUs and GPUs, with autodiff and without memory overflows.

Installing KeOps and getting started

The core of KeOps relies on a set of C++/CUDA routines. for which we provide bindings in the following languages

Python: installation instructions and examples
- numpy: doc
- pytorch: doc and tutorials
MATLAB: installation instructions and examples
R: coming soon...

Why using KeOps?

Scalable kernel operations

The very first motivation for KeOps was to compute fast and scalable Gaussian convolutions (aka. RBF kernel product). Given:

a target point cloud $(x_i)_{i=1}^N \in \mathbb R^{N \times D}$
a source point cloud $(y_j)_{j=1}^M \in \mathbb R^{M \times D}$
a signal or vector field $(b_j)_{j=1}^M \in \mathbb R^{M \times E}$ attached to the $y_j$'s

we strive to compute efficiently the array $(a_i)_{i=1}^N \in \mathbb R^{N \times E}$ given by

$$a_i = \sum_j K(x_i,y_j) b_j, \qquad i=1,\cdots,N$$

where $K(x_i,y_j) = \exp(-\|x_i - y_j\|^2 / \sigma^2)$. Another useful quantity that we need to compute is the derivative of $a_i$ with respect to the $x_i$'s,

$$a_i' = \sum_j K'(x_i,y_j) b_j, \qquad i=1,\cdots,N$$

where $K'(x_i,y_j) = \partial_x \exp(-\|x_i - y_j\|^2 / \sigma^2)$. KeOps allows you to compute both $a_i$ and $a_i'$ efficiently with its automatic differentiation module - that is, without needing to code explicitly the formula $K'(x_i,y_j) = -2(x_i - y_j) \exp(-\|x_i - y_j\|^2 / \sigma^2)$.

Today, KeOps can be used on a broad class of formulas as explained below.

High performances

In recent years, Deep Learning frameworks such as Theano, TensorFlow or PyTorch have evolved into fully-fledged applied math libraries: With negligible overhead, these tools now bring automatic differentiation and seamless GPU support to research communities used to array-centric frameworks -- Matlab and numpy.

Unfortunately, though, no magic is involved: optimised CUDA codes still have to be written for every atomic operation provided to end-users, and supporting all the standard mathematical computations thus comes at a huge engineering cost for the developers of the main frameworks. As of 2018, this considerable effort has been mostly restricted to the operations needed to implement Convolutional Neural Networks: linear algebra routines and grid convolutions. With KeOps, we are providing the brick that several research communities were missing.

The baseline example. A standard way of computing Gaussian convolutions in array-centric frameworks is to create and store in memory the full M-by-N kernel matrix $K_{i,j}=K(x_i,y_j)$, before computing $(a_i) = (K_{i,j}) (b_j)$ as a standard matrix product. Unfortunately, for large datasets (say, $M,N \geqslant 10,000$), this becomes intractable: large matrices just don't fit in GPU memories.

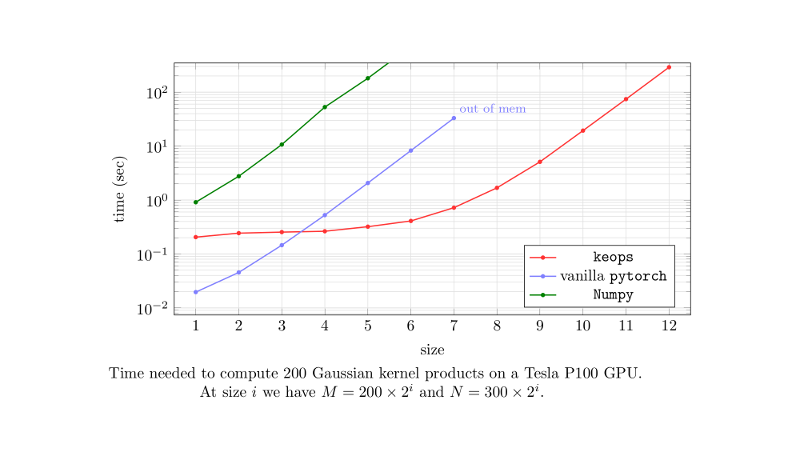
The purpose of KeOps, simply put, is to let users break through this memory bottleneck by computing online sum reductions:

A generic framework that fits your needs

KeOps supports generic operations, way beyond the simple case of kernel convolutions. Let's say that you have at hand:

a collection $p^1$, $p^2$, ..., $p^P$ of vectors.
a collection $x^1_i$, $x^2_i$, ..., $x^X_i$ of vector sequences, indexed by an integer $i$ ranging from 1 to N.
a collection $y^1_j$, $y^2_j$, ..., $y^Y_j$ of vector sequences, indexed by an integer $j$ ranging from 1 to M.
a vector-valued function $f(p^1, p^2,..., x^1_i, x^2_i,..., y^1_j, y^2_j, ...)$ on these input vectors.

Then, referring to the p's as parameters, the x's as x-variables and the y's as y-variables, the KeOps library allows you to compute efficiently any expression $a_i$ of the form

$$a_i = \text{Reduction}_{j=1,...,M} \big[ f(p^1, p^2,..., x^1_i, x^2_i,..., y^1_j, y^2_j, ...) \big], \qquad i=1,\cdots,N$$

alongside its derivatives with respect to all the variables and parameters.

As of today, we support:

Summation and (online, numerically stable) LogSumExp reductions.
Custom high-level ("gaussian(x,y) * (1+linear(u,v)**2)") and low-levels ("Exp(-G*SqDist(X,Y)) * ( IntCst(1) + Pow((U,V), 2) )") syntaxes to compute general formulas.
High-order derivatives with respect to all parameters and variables.
Non-radial kernels.

Related projects

We're currently investigating the possibility of developing a backend relying on an optimized CUDA library such as Tensor Comprehensions.

hrheydarian / libkeops