| title | author | date |
|---|---|---|
Controlling for student background |
Henrique |
15 de abril de 2018 |
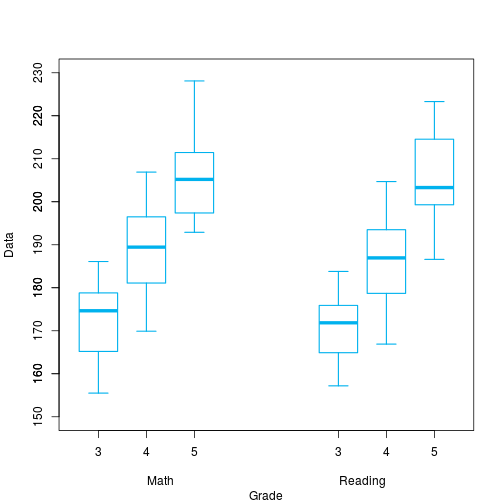
Inicialmente um boxplot que mostra os dados agrupados nas matérias de Matemática e Leitura para o terceiro quarto e quinto grau:
#Graph:1 - Boxplot
third_grade = read.csv("../input/third_grade.csv")
fourth_grade = read.csv("../input/fourth_grade.csv")
fifth_grade = read.csv("../input/fifth_grade.csv", na.strings="-")
print(third_grade)## School Math Reading X.Minority X.Poverty N
## 1 1 166.4 165.0 79.2 91.7 48
## 2 2 159.6 157.2 73.8 90.2 61
## 3 3 159.1 164.4 75.4 86.0 57
## 4 4 155.5 162.4 87.4 83.9 87
## 5 5 164.3 162.5 37.3 80.4 51
## 6 6 169.8 164.9 76.5 76.5 68
## 7 7 155.7 162.0 68.0 76.0 75
## 8 8 165.2 165.0 53.7 75.8 95
## 9 9 175.4 173.7 31.3 75.6 45
## 10 10 178.1 171.0 13.9 75.0 36
## 11 11 167.1 169.4 36.7 74.7 79
## 12 12 177.1 172.9 26.5 63.2 68
## 13 13 174.2 172.7 28.3 52.9 191
## 14 14 175.6 174.9 23.7 48.5 97
## 15 15 170.8 174.9 14.5 39.1 110
## 16 16 175.1 170.1 25.6 38.4 86
## 17 17 182.8 181.4 22.9 34.3 70
## 18 18 180.3 180.6 15.8 30.3 165
## 19 19 178.8 178.0 14.6 30.3 89
## 20 20 181.4 175.9 28.6 29.6 98
## 21 21 182.8 181.6 21.4 26.5 98
## 22 22 186.1 183.8 12.3 13.8 130
print(fourth_grade)## School Math Reading X.Minority X.Poverty N
## 1 1 181.1 177.0 78.9 89.5 38
## 2 2 181.1 173.8 75.9 79.6 54
## 3 3 180.9 175.5 64.1 71.9 64
## 4 4 169.9 166.9 94.4 91.7 72
## 5 5 183.6 178.7 38.6 61.4 57
## 6 6 178.6 170.3 67.9 83.9 56
## 7 7 182.7 178.8 65.8 63.3 79
## 8 8 186.1 180.9 48.0 64.7 102
## 9 9 187.2 187.3 33.3 62.7 51
## 10 10 194.5 188.9 11.1 77.8 36
## 11 11 180.3 181.7 47.4 70.5 78
## 12 12 187.6 186.3 19.4 59.7 72
## 13 13 194.0 189.8 21.6 46.2 171
## 14 14 193.1 189.4 28.8 36.9 111
## 15 15 195.5 188.0 20.2 38.3 94
## 16 16 191.3 186.6 39.7 47.4 78
## 17 17 200.1 199.7 23.9 23.9 67
## 18 18 196.5 193.5 22.4 32.8 116
## 19 19 203.5 204.7 16.0 11.7 94
## 20 20 199.6 195.9 31.1 33.3 90
## 21 21 203.3 194.9 23.3 25.9 116
## 22 22 206.9 202.5 13.1 14.8 122
print(fifth_grade)## School Math Reading X.Minority X.Poverty N
## 1 1 197.1 186.6 81.0 92.9 42
## 2 2 194.9 200.1 83.3 88.1 42
## 3 3 192.9 194.5 56.0 80.0 50
## 4 4 193.3 189.9 92.6 75.9 54
## 5 5 197.7 199.6 21.7 67.4 46
## 6 6 193.2 193.6 70.4 76.1 71
## 7 7 198.0 200.9 64.1 67.9 78
## 8 8 205.2 203.5 45.5 61.0 77
## 9 9 210.2 223.3 34.7 73.5 49
## 10 10 204.8 199.0 29.4 55.9 34
## 11 11 205.7 202.8 42.3 71.2 52
## 12 12 201.2 207.8 15.8 51.3 76
## 13 13 205.2 203.3 19.8 41.2 131
## 14 14 212.7 211.4 26.7 41.6 101
## 15 15 NA NA NA NA NA
## 16 16 209.6 206.5 22.4 37.3 67
## 17 17 223.5 217.7 14.3 30.2 63
## 18 18 222.8 218.0 16.8 24.8 137
## 19 19 NA NA NA NA NA
## 20 20 228.1 222.4 20.6 23.5 102
## 21 21 221.0 221.0 10.5 13.2 114
## 22 22 NA NA NA NA NA
boxplot(third_grade$Math, fourth_grade$Math, fifth_grade$Math, third_grade$Reading,
fourth_grade$Reading, fifth_grade$Reading,names = c("3","4", "5", "3","4", "5"),
xlab="Math\t\t\t\t\t\t\tReading", ylab="Data", ylim=c(150,230), at=c(1,2,3,6,7,8),
border="deepskyblue2", lty=1, lwd=1.5)
axis(2,at=c(150,160,170,180,190,200,210,220,230))
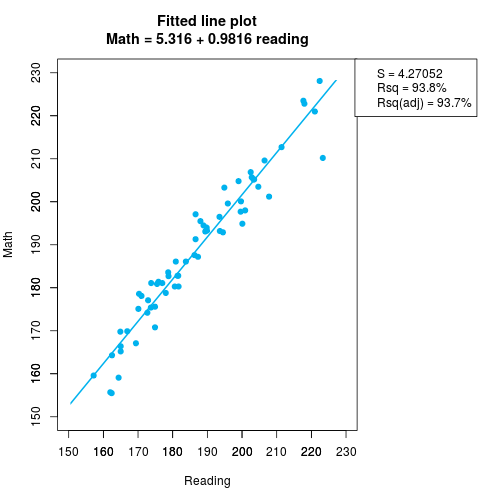
title(xlab = "Grade", line = 4)Depois plotamos um gráfico que mostra a correlação entre as variáveis matemática e leitura. Podemos observar uma alta correlação entre os dados.
#Graph:2 - Math vs Reading
third_grade = read.csv("../input/third_grade.csv")
fourth_grade = read.csv("../input/fourth_grade.csv")
fifth_grade = read.csv("../input/fifth_grade.csv", na.strings="-")
math_array <- c(third_grade$Math, fourth_grade$Math, fifth_grade$Math)
reading_array <- c(third_grade$Reading, fourth_grade$Reading, fifth_grade$Reading)
max_math <- max(math_array, na.rm=TRUE)
max_reading <- max(reading_array, na.rm=TRUE)
min_math <- min(math_array, na.rm=TRUE)
min_reading <- min(reading_array, na.rm=TRUE)
scale <- c(150,160,170,180,190,200,210,220,230)
min_max <- c(150,230)
#This line is used to use legend out of plot area.
par(mar=c(5.1, 4, 4.1, 10.2), xpd=TRUE)
#Plot data, insert title, define axis range and set the legend
plot(reading_array, math_array, xlim=min_max, ylim=min_max, xlab="Reading",
ylab="Math", col="deepskyblue2", pch=19)
title(main="Fitted line plot\nMath = 5.316 + 0.9816 reading")
axis(1, at=scale)
axis(2, at=scale)
legend("topright", inset=c(-0.4,0),
legend=c("S = 4.27052","Rsq = 93.8%", "Rsq(adj) = 93.7%"))
#Create a square do delimit plot area.
clip(min_math-5, max_math+5, min_reading-5, max_reading+5)
#Create a line
linear_regression <- lm(math_array~reading_array)
abline(linear_regression$coefficients[1], linear_regression$coefficients[2],
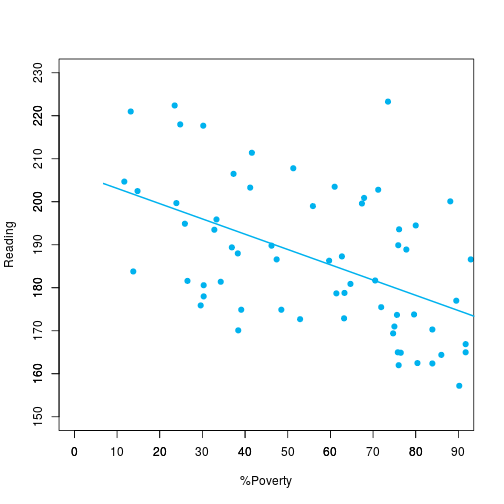
col="deepskyblue2", lwd=2)Já que matemática e leitura são altamente correlatas, então foi escolhido o atributo leitura para verificar a correlação com as outros atributos (pobreza e minoria) ambos em porcentagem.
#Graph:3 - Reading vs X.Poverty
third_grade = read.csv("../input/third_grade.csv")
fourth_grade = read.csv("../input/fourth_grade.csv")
fifth_grade = read.csv("../input/fifth_grade.csv", na.strings="-")
poverty_array <- c(third_grade$X.Poverty, fourth_grade$X.Poverty, fifth_grade$X.Poverty)
reading_array <- c(third_grade$Reading, fourth_grade$Reading, fifth_grade$Reading)
max_poverty <- max(poverty_array, na.rm=TRUE)
max_reading <- max(reading_array, na.rm=TRUE)
min_poverty <- min(poverty_array, na.rm=TRUE)
min_reading <- min(reading_array, na.rm=TRUE)
x_scale <- c(0,10,20,30,40,50,60,70,80,90)
y_scale <- c(150,160,170,180,190,200,210,220,230)
min_max_x <- c(0,90)
min_max_y <- c(150,230)
#Plot data, insert title, define axis range and set the legend
plot(poverty_array, reading_array, xlim=min_max_x, ylim=min_max_y, xlab="%Poverty",
ylab="Reading", col="deepskyblue2", pch=19)
axis(1, at=x_scale)
axis(2, at=y_scale)
#Create a square do delimit plot area.
clip(min_poverty-5, max_poverty+5, min_reading-5, max_reading+5)
#Create a line
linear_regression <- lm(reading_array~poverty_array)
abline(linear_regression$coefficients[1], linear_regression$coefficients[2],
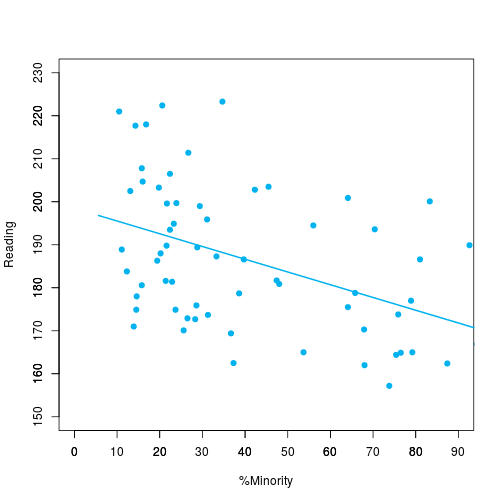
col="deepskyblue2", lwd=2)#Graph:4 - Reading vs X.Minority
third_grade = read.csv("../input/third_grade.csv")
fourth_grade = read.csv("../input/fourth_grade.csv")
fifth_grade = read.csv("../input/fifth_grade.csv", na.strings="-")
minority_array <- c(third_grade$X.Minority, fourth_grade$X.Minority, fifth_grade$X.Minority)
reading_array <- c(third_grade$Reading, fourth_grade$Reading, fifth_grade$Reading)
max_minority <- max(minority_array, na.rm=TRUE)
max_reading <- max(reading_array, na.rm=TRUE)
min_minority <- min(minority_array, na.rm=TRUE)
min_reading <- min(reading_array, na.rm=TRUE)
x_scale <- c(0,10,20,30,40,50,60,70,80,90)
y_scale <- c(150,160,170,180,190,200,210,220,230)
min_max_x <- c(0,90)
min_max_y <- c(150,230)
#Plot data, insert title, define axis range and set the legend
plot(minority_array, reading_array, xlim=min_max_x, ylim=min_max_y, xlab="%Minority",
ylab="Reading", col="deepskyblue2", pch=19)
axis(1, at=x_scale)
axis(2, at=y_scale)
#Create a square do delimit plot area.
clip(min_minority-5, max_minority+5, min_reading-5, max_reading+5)
#Create a line
linear_regression <- lm(reading_array~minority_array)
abline(linear_regression$coefficients[1], linear_regression$coefficients[2],
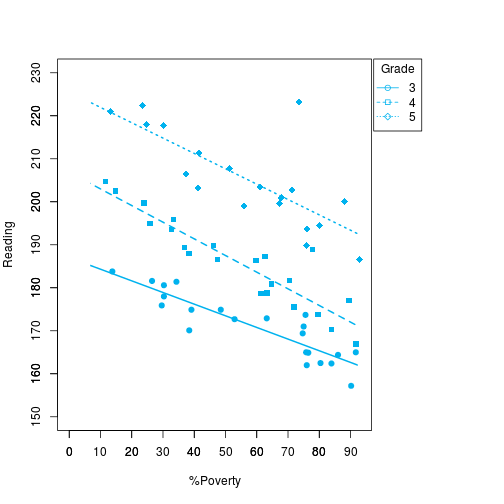
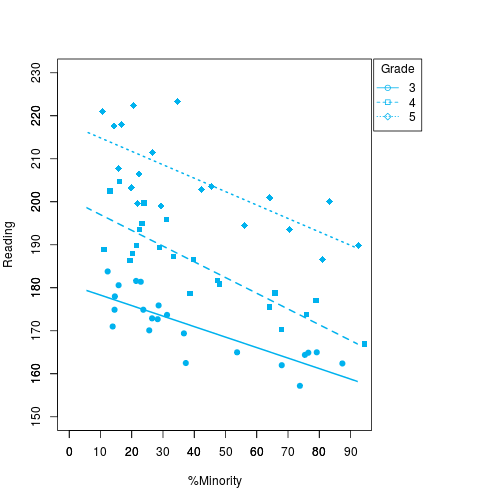
col="deepskyblue2", lwd=2)Podemos ver que há uma tendência das variáveis serem inversamente correlatas, no entanto, não é tão precisa. Dessa forma, vamos traçar a correlação por grau de escolaridade entre essas variáveis.
#Graph:5 - Reading vs X.Poverty vs Grade
third_grade = read.csv("../input/third_grade.csv")
fourth_grade = read.csv("../input/fourth_grade.csv")
fifth_grade = read.csv("../input/fifth_grade.csv", na.strings="-")
x_scale <- c(0,10,20,30,40,50,60,70,80,90)
y_scale <- c(150,160,170,180,190,200,210,220,230)
min_max_x <- c(0,93)
min_max_y <- c(150,230)
#This line is used to use legend out of plot area.
par(mar=c(5.1, 4, 4.1, 9.2), xpd=TRUE)
#Plot data, insert title, define axis range and set the legend
plot(third_grade$X.Poverty, third_grade$Reading, xlim=min_max_x, ylim=min_max_y,
xlab="%Poverty", ylab="Reading", col="deepskyblue2", pch=19)
axis(1, at=x_scale)
axis(2, at=y_scale)
legend("topright", inset=c(-0.16,0), pch=c(21:23),
legend=c(3,4,5), lty=1:3, col="deepskyblue2", title="Grade")
#Plot another points (4-th and 5-th grade)
points(fourth_grade$X.Poverty, fourth_grade$Reading, col="deepskyblue2",
pch=15)
points(fifth_grade$X.Poverty, fifth_grade$Reading, col="deepskyblue2",
pch=18, cex=1.3)
#Create a square do delimit plot area.
clip(min_poverty-5, 92, min_reading-5, 230)
#Create lines
linear_regression <- lm(third_grade$Reading ~ third_grade$X.Poverty)
abline(linear_regression$coefficients[1], linear_regression$coefficients[2],
col="deepskyblue2", lwd=2)
linear_regression <- lm(fourth_grade$Reading ~ fourth_grade$X.Poverty)
abline(linear_regression$coefficients[1], linear_regression$coefficients[2],
col="deepskyblue2", lwd=2, lty=2)
linear_regression <- lm(fifth_grade$Reading ~ fifth_grade$X.Poverty)
abline(linear_regression$coefficients[1], linear_regression$coefficients[2],
col="deepskyblue2", lwd=2, lty=3)#Graph:6 - Reading vs X.Minority vs Grade
third_grade = read.csv("../input/third_grade.csv")
fourth_grade = read.csv("../input/fourth_grade.csv")
fifth_grade = read.csv("../input/fifth_grade.csv", na.strings="-")
x_scale <- c(0,10,20,30,40,50,60,70,80,90)
y_scale <- c(150,160,170,180,190,200,210,220,230)
min_max_x <- c(0,93)
min_max_y <- c(150,230)
#This line is used to use legend out of plot area.
par(mar=c(5.1, 4, 4.1, 9.2), xpd=TRUE)
#Plot data, insert title, define axis range and set the legend
plot(third_grade$X.Minority, third_grade$Reading, xlim=min_max_x, ylim=min_max_y,
xlab="%Minority", ylab="Reading", col="deepskyblue2", pch=19)
axis(1, at=x_scale)
axis(2, at=y_scale)
legend("topright", inset=c(-0.16,0), pch=c(21:23),
legend=c(3,4,5), lty=1:3, col="deepskyblue2", title="Grade")
#Plot another points (4-th and 5-th grade)
points(fourth_grade$X.Minority, fourth_grade$Reading, col="deepskyblue2",
pch=15)
points(fifth_grade$X.Minority, fifth_grade$Reading, col="deepskyblue2",
pch=18, cex=1.3)
#Create a square do delimit plot area.
clip(min_minority-5, 92, min_reading-5, 230)
#Create lines
linear_regression <- lm(third_grade$Reading ~ third_grade$X.Minority)
abline(linear_regression$coefficients[1], linear_regression$coefficients[2],
col="deepskyblue2", lwd=2)
linear_regression <- lm(fourth_grade$Reading ~ fourth_grade$X.Minority)
abline(linear_regression$coefficients[1], linear_regression$coefficients[2],
col="deepskyblue2", lwd=2, lty=2)
linear_regression <- lm(fifth_grade$Reading ~ fifth_grade$X.Minority)
abline(linear_regression$coefficients[1], linear_regression$coefficients[2],
col="deepskyblue2", lwd=2, lty=3)O próximo passo é montar uma matriz de correlações entre a variável de leitura para as variáveis de minoria e pobreza para cada grau.
#Tab:1 - Correlation
third_grade = read.csv("../input/third_grade.csv")
fourth_grade = read.csv("../input/fourth_grade.csv")
fifth_grade = read.csv("../input/fifth_grade.csv", na.strings="-")
minority_3 <- cor(third_grade$X.Minority, third_grade$Reading,
method="pearson")
minority_4 <- cor(fourth_grade$X.Minority, fourth_grade$Reading,
method="pearson")
minority_5 <- cor(fifth_grade$X.Minority, fifth_grade$Reading,
method="pearson", use = "complete.obs")
poverty_3 <- cor(third_grade$X.Poverty, third_grade$Reading,
method="pearson")
poverty_4 <- cor(fourth_grade$X.Poverty, fourth_grade$Reading,
method="pearson")
poverty_5 <- cor(fifth_grade$X.Poverty, fifth_grade$Reading,
method="pearson", use = "complete.obs")
cor_between <- c('Reading scores and', '%minority', '%poverty')
third_grade <- c('', format(round(minority_3, 2), nsmall = 2),
format(round(poverty_3, 2), nsmall = 2))
fourth_grade <- c('', format(round(minority_4, 2), nsmall = 2),
format(round(poverty_4, 2), nsmall = 2))
fifth_grade <- c('', format(round(minority_5, 2), nsmall = 2),
format(round(poverty_5, 2), nsmall = 2))
cor_data_frame <- data.frame(cor_between, third_grade, fourth_grade, fifth_grade)
colnames(cor_data_frame) <- c('Correlation between', '3rd Grade', '4th Grade', '5th Grade')
print(cor_data_frame)## Correlation between 3rd Grade 4th Grade 5th Grade
## 1 Reading scores and
## 2 %minority -0.83 -0.87 -0.75
## 3 %poverty -0.89 -0.92 -0.76