Visualization of COVID-19 Confirmed Cases for Austria

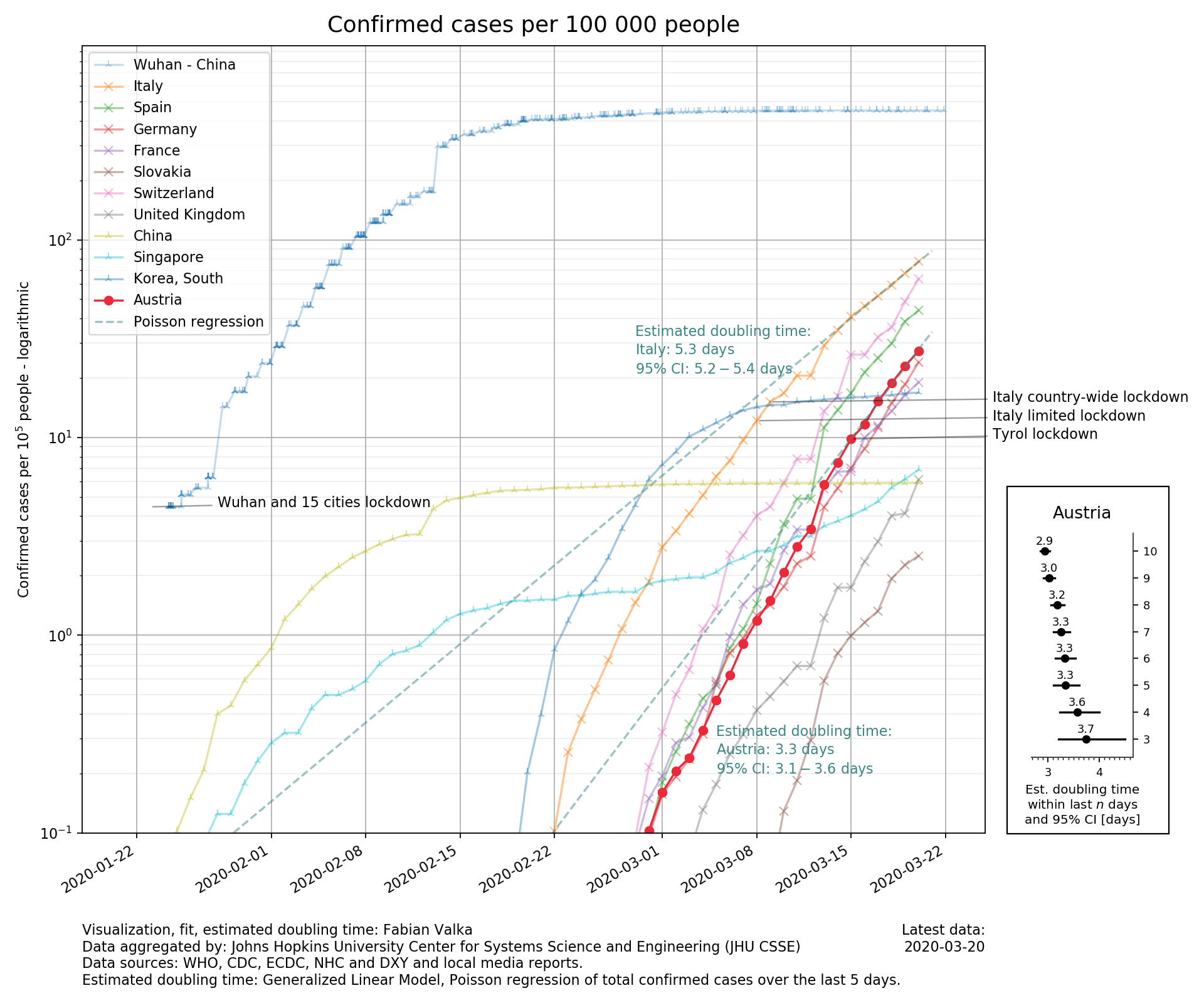
This Jupyter notebook produces a log-scaled plot of confirmed cases per 10^5 people for different countries, with a focus on Austria.

Warning! Read this

I'm not an expert in medicine, epidemiology, biology or similar
This style has been mostly developed for me and my friends, mostly people with graduate level degrees in science or technology and might not at all be suitable for the general public!
The code may contain bugs, is not well verified or tested
The assumptions about the fit might be completely wrong
Use at your own risk and consider the implications of publishing the visualization and whom you publish it to

Visualize Responsibly

Please read those excellent articles on the Tableau blog:

10 considerations before you create another chart about COVID-19
[What the BBC got wrong in their Covid-19 visualization] https://www.tableau.com/about/blog/2020/3/covid-19-resources-data-viz-best-practices

Do this if you use it!

Update your visualization regularly
Verify each output by hand with primary sources for your country
Look for mistakes and open an issue or pull request

Example Output

Data Sources

John Hopkins University CSSE Aggregated Data

Primarily data from the John Hopkins Universities Center for System Science and Engineering GitHub repository on COVID-19 is used in the plot. Actually all lines, except for "Wuhan - China" are plotted based upon this dataset.

Doubling Time Estimation

The doubling time and its confidence interval are estimated using a generalized linear model fitting of a Poisson regression (log-normal) model to the cumulative cases using maximum likelihood estimation.

Satsmodels GLM module is used as the software implementation.

Our log-linear model for the cumulative case count y at day x is:

$\log{y} = \beta_0 + \beta x$

Using this module the fitted function form is:

$f(x) = e^{\beta_0 + \beta x}$

This is formulated in patsy as

y ~ x

Doubling time estimates, as well as the confidence intervals in doubling time estimates are obtained by calculating the doubling time from the exponential functions slope parameter.

$T_d = \frac{\log{2}}{\beta}$

Installation

Install python >= 3.6 and Jupyter notebook
Install required python packages

pip install -r requirements.txt

Download the data repositories using git clone, as described in the data/README.md file.

haraldschilly / covid19-austria-visualization