githubharald / fast_inv_sqrt

Fast approximation of the inverse square root 1/√(x).

Fast Inverse Square Root

This repository implements a fast approximation of the inverse square root: 1/√(x). It is a simplified version of the famous hack used in the 3D game Quake in the 90s.

Get started

Code snippet

If you just need the code, simply copy and paste the following code snippet.

#include <cstdint>
#include <cstddef>

float fast_inv_sqrt(float x)
{
    float y = x; // y holds the current guess for 1/sqrt(x)
    uint32_t *i = reinterpret_cast<uint32_t *>(&y); // i points to current guess y

    const uint32_t exp_mask = 0x7F800000; // 0xFF<<23
    const uint32_t magic_number = 0x5f000000; // 190<<23

    // initial guess using magic number
    *i = magic_number - ((*i >> 1) & exp_mask);

    // refine guess using small number of Newton iterations
    const size_t num_newton_iter = 2;
    for (size_t i = 0; i < num_newton_iter; ++i)
    {
        y = (x * y * y + 1) / (2 * x * y);
    }

    return y;
}

Analyze algorithm

• Go to src/
• Compile the C++ code, e.g. g++ -O2 fast_inv_sqrt.cpp, this creates a binary
• Execute the binary, which produces a file "dump.csv"
• Execute the Python script, e.g. python3 analyze.py, this shows the plots

Error

The algorithm performs two steps:

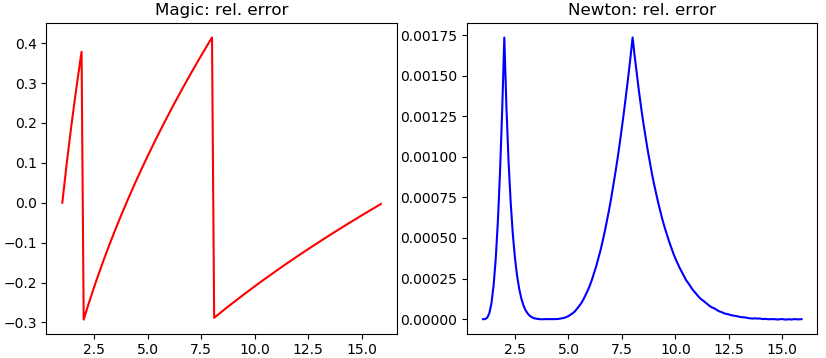
• Apply "bit-magic" to compute an initial guess with at most 41% relative error
• Apply 2 iterations of Newton's method to drive the maximum relative error down to <0.2%

The plot shows the relative error after each of the two steps for x values from 1 to 16. For more details see this article.