Tempo e consumo de memória, respectivamente Complexidade de Tempo e de espaço
Por que a medida de tempo em segundos não representa qualificadamente o tempo de execução de um algoritmo?
Pois o tempo de execução de um algoritmo ou método da estrutura de dados é afetado pelo ambiente de hardware (compilador, processador, Sistema operacional, linguagem de programaçāo, etc) e tamanho da entrada.
Medição de tempo em segundos não é uma medida estável e de qualidade.
A medida deve ser independente de tecnologia (software ou hardware)
A medição de tempo é feita através da quantidade de passos que o algoritmo precisa para finalizar sua execução.
O tamanho da entrada.
Da logarítmica e da exponencial é 2.
É escolhido 2 pois representa valor binário.
De M. É a função f: N -> N, onde f(n) é o número máximo de passos que M usa sobre entradas de comprimento n. É um costume generalizado usar n para representar o comprimento de entrada.
Dado dois algoritmos A e B com as complexidades de tempo respectivamente f1 e f2, qual é o melhor algoritmo? O que indica qual é o melhor algoritmo?
O algoritmo com a menor complexidade de tempo é o melhor. O algoritmo que tiver a função com o menor valor representa uma solução, ou seja, o algoritmo precisa de menos tempo ou passsos para resolver o problema.
Representa o comprimento de entrada.
- Atribuição de valores a variáveis
- Chamadas de métodos
- Operações aritméticas (por exemplo, adição de dois números)
- Comparação de dois números
- Acesso a um arranjo
- Seguimento de uma referência para um objeto
- Retorno de um método
O valor que se atribui é 1.
Desenvolva o pseudocódigo do algoritmo SOMA, que realiza a soma de dois números inteiros recebidos por parâmetro e tem como saída a resultado da operação. Identifique a sua função de complexidade de tempo.
soma (a, b) {
return a + b;
}
soma(1,2);| soma(a, b): | Custo | Vezes |
|---|---|---|
| s <- a + b | c1 | 1 |
| retorna s | c2 | 1 |
f(n) = c1 * 1 + c2 * 1
f(n) = 1 * 1 + 1 * 1
f(n) = 1 + 1
f(n) = 2
Desenvolva o pseudocódigo do algoritmo SOMA_VETOR, que realiza a soma de todos os elementos de um vetor. O algoritmo recebe o vetor V e tem como saída o resultado. Identifique a sua função de complexidade de tempo.
soma(vetor) {
let soma = 0;
for (let i = 0; i <= vetor.length; i++) {
soma += vetor[i];
}
return soma;
}
soma([1,2,3,4,5,6]);| soma(vetor): | Custo | Vezes |
|---|---|---|
| s <- 0 | c1 | 1 |
| para i <- 1 até vetor.tamanho | c2 | n |
| s <- s + vetor[i] | c3 | n |
| i <- i + 1 | c4 | n |
| retorna s | c5 | 1 |
f(n) = c1 * 1 + c2 * n + c3 * n + c4 * n + c5 + 1
f(n) = 1 * 1 + 1 * n + 1 * n + 1 * n + 1 * 1
f(n) = 1 + n + n + n + 1
f(n) = 3n + 2
Desenvolva o pseudocódigo do algoritmo CONTAGEM_IMPARES, que realiza a contagem de números impares de um vetor. O algoritmo recebe o vetor V e tem como saída o resultado. Identifique a sua função de complexidade de tempo.
soma(vetor) {
let soma = 0;
for (let i = 0; i <= vetor.length; i++) {
if (vetor[i]%2 != 0) {
soma += vetor[i];
}
}
return soma;
}
soma([1,2,3,4,5,6]);| soma(vetor): | Custo | Vezes |
|---|---|---|
| s <- 0 | c1 | 1 |
| para i <- 1 até vetor.tamanho | c2 | n |
| se vetor[i] %2!= 0 entao | c3 | n |
| s <- s + vetor[i] | c4 | n |
| i <- i + 1 | c5 | n |
| retorna s | c6 | 1 |
f(n) = c1 * 1 + c2 * n + c3 * n + c4 * n + c5 * n + c6 * 1
f(n) = 1 * 1 + 1 * n + 1 * n + 1 * n + 1 * n + 1 * 1
f(n) = 1 + n + n + n + n + 1
f(n) = 4n + 2
Desenvolva o pseudocódigo do algoritmo SOMA_MATRIZ, que realiza a soma de todos os elementos de uma matriz. O algoritmo recebe a matriz M e tem como saída o resultado. Identifique a sua função de complexidade de tempo.
soma(matriz) {
let soma = 0;
for (let i = 0; i <= matriz.length; i++) {
for (let j = 0; j <= matriz[i]; j++) {
soma += matriz[i][j];
}
}
return soma;
}
soma([[1,2],[2,3],[3,4],[4,5],[5,6],[6,7]]);| soma(matriz): | Custo | Vezes |
|---|---|---|
| s <- 0 | c1 | 1 |
| para i <- 1 até matriz.tamanho | c2 | n |
| para j <- 1 até matriz[i].tamanho | c3 | n * n |
| s <- s + matriz[i][j] | c4 | n * n |
| j <- j + 1 | c5 | n * n |
| i <- i + 1 | c6 | n |
| retorna s | c7 | 1 |
f(n) = c1 * 1 + c2 * n + c3 * nn + c4 * nn + c5 * nn + c6 * n + c7 * 1
f(n) = 1 * 1 + 1 * n + 1 * n² + 1 * n² + 1 * n² + 1 * n + 1 * 1
f(n) = 1 + n + n² + n² + n² + n + 1
f(n) = 3n² + 2n + 2
Desenvolva o pseudocódigo do algoritmo BUSCA_MATRIZ, que identifica posição x e y de um elemento em uma matriz. O algoritmo recebe a matriz M e o valor V e tem como saída a posição x e y . Identifique a sua função de complexidade de tempo.
buscaMatriz(matriz, valor) {
for (let i = 0; i <= matriz.length; i++) {
for (let j = 0; j <= matriz[i]; j++) {
if (matriz[i][j] == valor) {
return [i, j];
}
}
}
return null;
}
buscaMatriz([[1,2],[2,3],[3,4],[4,5],[5,6],[6,7]], 2);| buscaMatriz(matriz, valor): | Custo | Vezes |
|---|---|---|
| para i <- 1 até matriz.tamanho | c1 | n |
| para j <- 1 até matriz[i].tamanho | c2 | n * n |
| se matriz[i][j] == valor | c3 | n * n |
| retorna [i,j] | c4 | 1 |
| j <- j + 1 | c5 | n * n |
| i <- i + 1 | c6 | n |
| retorna s | c7 | 1 |
f(n) = c1 * n + c2 * nn + c3 * nn + c4 * 1 + c5 * nn + c6 * n + c7 *1
f(n) = 1 * n + 1 * n² + 1 * n² + 1 * 1 + 1 * n² + 1 * n + 1 * 1
f(n) = n + n² + n² + 1 + n² + n + 1
f(n) = 3n² + 2n + 2
O tempo exato de um algoritmo é frequentemente uma expressão complexa. Tanto para identificar como para calcular.
Compreender o tempo de execução para entradas grandes, ou seja, é um método de descrever o comportamento de limites.
- f(n) = 6n³ + 2n² + 20n + 45
- Identificar o componente de maior ordem: 6n³
- Ignorar os coeficientes = n³
Dizemos que f é assintoticamente no máximo n³.
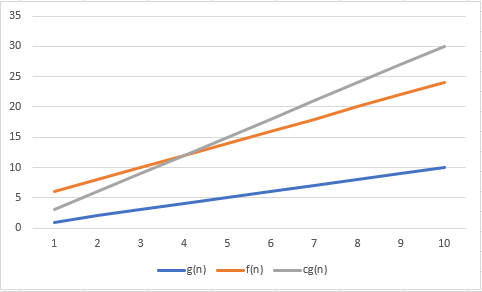
A notação assintótica ou notação O-grande (Big-Oh) é usada para descrever o relacionamento é f(n) = O(n3). Formalmente definimos como: Onde R+ é o conjunto dos reais não negativos
Diz que uma função é menor que ou igual a outra função g(n). x Ou seja, f é limitada superiormente por g (até no máximo um fator constante) assintoticamente.
Sejam f e g funções f,g : N → R+. Digamos que f(n) = O(g(n)) se existem inteiros positivos c e n0 tais que para todo inteiro n ≥ n0
Quando f(n) = O(g(n)) dizemos que g(n) é o limite superior para f(n) ou, mais precisamente, que g(n) é um limitante assintótico para f(n), para enfatizar que estamos suprimento fatores constantes.
Crie um gráfico explicando a notação O-grande. Utilize f(n) = 2n + 4. Qual é um valor possível para n0?
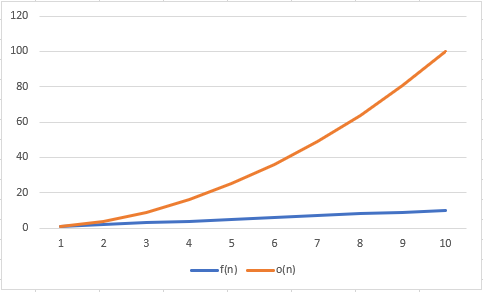
A notação o-–pequeno diz que uma função é menor que a outra função g(n). Ou seja, f é dominada por g assintoticamente.
Formalmente definimos como: Onde R+ é o conjunto dos reais não negativos.
O(n)
o(n²)
O(1)
o(n)
O(n²)
o(2 ^ n)
O(logn)
o(n²)
O(n!)
o(n!²)
O(n³)
o(n!)
O(5 ^ n)
o(n * n!)
O(logn)
o(n²)
O(1) o(n)
O(n) o(nlogn)
O(n) o(n²)
O(n²) o(n!)
O(n²) o(2 ^ n)