For over 70 years, spatial interaction models (SIMs) have been a key tool to simulate flows between entities at different locations in physical space. SIMs represent mathematical formulations through which the spatial interaction between geographic places encoded in aggregate flows of people, information and goods can be rendered. Intuitively, these models seek to represent the spatial interaction between places as a function of three components: origin characteristics, destination characteristics and the separation between origins and destinations. Originally adapted from physics, spatial flows between an origin and a destination were conceived to be proportional to their gravitational force and inversely related to their spatial separation. Characteristics of origins and destinations are used to represent gravitational forces pushing and/or pulling people, information and goods from and to specific locations, and different forms of distance and costs are used to represent the deterring effects of geographical separation on spatial flows.
SIMs have been applied in a wide range of contexts to support data analysis and decision making in retail, transport, housing, epidemiology, public health, land use, urban and population modelling and planning projection and forecasting contexts. SIMs are generally used for two key purposes: prediction and inference. The prediction of the size and direction of spatial flows has been used to predict the impact of new service units, such as shopping stores, healthcare facilities and housing units on the potential demand for associated services and traffic patterns. Predictions from such analyses enable the identification of optimal locations and size for potential new service units. A second key purpose of SIMs is inference about the factors shaping the spatial interactions in a network of flows. SIMs have been used to determine and understand the influence of retail store on consumers’ store choices and place attributes on migration decisions and commuting patterns. SIMs have also been used to delineate geographical areas of service and retail catchment areas.
Formally SIMs take different forms. Newtonian gravity models are
probably the most widely known and used form of spatial interaction
models in social sciences. Adapted from physics, the basic gravity model
assumes that the interactions
between an origin
and a destination
in the form of flows can be understood as a function of driving forces
like masses
and
, and a measure of spatial separation
. Areas are assumed to interact in a positively reinforcing way that is
multiplicative of their masses, and at the same time their interactions
are expected to diminish with the intervening role of spatial
separation. Spatial separation is generally measured by distance, cost
or time involved in the interaction, and is often represented by a
distance-decay function. In human systems the model generally also
incorporates a
constant ensuring that expected flows do not exceed observed totals, and
parameter representing the deterring effect of spatial separation, or
distance. The key task in a gravity model is to estimate these
parameters
(i.e.
and
). A typical notation for the model is:
In practice, a matrix of flows, between a set of origins, a set of destinations and a measure of spatial separation between origins and destinations, is the key input for SIMs. A family of SIMs encapsulating four distinctive shapes is typically considered (Wilson 1971). An unconstrained formulation of the model is actually constrained to ensure that the total sum of the predicted flows from a gravity model be equal the total sum of the observed flows across all origins and destinations. Constrained versions are used to ensure that specific origin or destination observations are met. Three general formulations of constrained models are used: production-constrained, attraction-constrained and doubly constrained models. Production-constrained forms are used to constrain a model so that the predicted number of trips emanating from each origin is equal to the observed number of trips. Attraction-constrained forms do the same but at the destination. Doubly constrained models combine these two sets of constraints.
SIMs have been extended in six key ways. First, social science theory has been infused to underpin and enrich SIMs. SIMs were originally conceptualised as a mathematical formulation to represent observed relationships between origins and destinations encoded in a origin-destination matrix, and generate accurate prediction of spatial flows. Field-specific theories have been used to extend and develop the fundamental structure of SIMs to understand retail, trade, transport, communication, migration and mobility patterns. Second, more sophisticated measures to capture the influence of origins and destinations have been developed. The specification of SIMs has moved away from relying on population size to approximate the propulsive effect of origins and attractive force of destinations, to capture local economic, political, cultural and social differences across origins and destination, and recognise propulsive and attractive effects at play in both origins and destinations. Third, measures of spatial separation have also been refined to more appropriately reflect the geographical, physiological and financial distance and costs between origins and destinations (Schwartz 1973). It is now much easier to calculate route distances on road networks thanks to routing engines and interfaces to routing engines from languages in which SIMs can be developed Morgan et al. (2019). Many innovations are possible thanks to new datasets, for example the use of night-time light intensity to estimate the spatial distribution of human settlements (Niedomysl et al. 2017), and the use of aggregated datasets derived from social media sources to train SIMs (Lovelace et al. 2014). Fourth, considerable methodological work has been done to conceptualise and operationalise the influence of spatial structure in SIMs (Oshan 2021). Fifth, generalisable approaches have been proposed to account for spatial structure in distinctive ways: the competing destination model by including an accessibility measure (A. S. Fotheringham 1983); the Box–Cox transform by using a Box–Cox functional form of distance
; spatial choice modelling by accounting for destination alternative substitution patterns (Hunt, Boots, and Kanaroglou 2004); spatial econometric modelling
; and eigenvector spatial filtering by incorporating spatial dependence or spatial autocorrelation
. Fifth, frameworks to calibrate SIMs have evolved. Early methods of calibration comprised linear programming and non-linear optimization. Regression methods have now become prominent evolving from linear log-normal model formulations using ordinary least squares (OLS) and maximum likelihood estimation procedures, through generalised linear frameworks using iteratively reweighted least squares (IWLS), especially Poisson and Negative Binomial distributions
, to more sophisticated multilevel and discrete choice models to capture origin-, destination- or origin-destination-specific parameters
. Sixth, alternative frameworks of spatial interaction modelling have been developed to incorporate different ways of conceptualising the decision-making process of choosing a destination location. The radiation (Simini et al. 2012), exploration and preferential return (Pappalardo et al. 2015) and random utility models (McFadden 1974) have become prominent frameworks to model spatial flows, particularly human mobility flows.
Thus, considerable progress has been made on advancing the theoretical and methodological underpinnings of SIMs. Yet, major challenges remain in terms of reproducibility, calibration and Big Data modelling. We believe that addressing these challenges are key to facilitate the application of SIMs, extend existing modelling approaches, leverage the greater geographical and temporal breadth, depth, scale and timeliness of Big Data and ultimately enhance our understanding human interactions and our social world.
In this section, we want to describe why the areas identified are seen as challenges and in which ways.
Reproducibility of SIMs has not been a prominent area of attention in past research. Replicating most SIM application would certainly be a challenge. Such situation is unfortunate as it is likely to have limited the applicability and portability of sophisticated frameworks to estimate SIMs and capture the effects of spatial structure on spatial flows. In fact many sophisticated SIMs have been developed to capture the effects of spatial structure on spatial flows, but the accessibility and applicability of such models remained limited. Arguably even the application of basic formulations of SIMs tends to represent a daunting challenge for beginning modelers of spatial flow data. The lack of reproducibility as a standard research practice has tended to generate “black box” data analyses, preventing the validation, verification and comparability of SIM estimates.
Understandably, reproducibility was not concern during the 1970s and 1980s, when significant progress was made on developing SIMs. Computer hardware, software and know-how needed to develop and deploy SIMs were unavailable to most people. Even when consumer laptops became widely available and more affordable during the 2000s, few well-known user-friendly off-the-shelf options to implement SIMs existed. Yet, today, computer software and hardware are highly affordable and learning computing programming has become increasingly accessible. With the advent of open science, resources to learn computer programming in popular data science languages, such as R and Python have become widely available. Nevertheless, most SIM applications cannot still be reproduced.
Yet, reproducibility of SIM estimates can yield key benefits for future research, impact and training . Reproducible research can boots citations and facilitate comparability of research results enabling the application of existing methods to a wide range of contexts (Brunsdon 2016). Reproducibility can also enhance accountability, validation and verification of research findings by increasing transparency Brunsdon (2016). By transparently sharing open data products, including reproducible code and input data (Arribas-Bel et al. 2021), used in the analysis, results can be validated and lessons can be learnt from the limitations and strengths of the application of particular methods. Reproducible open products can also increase the portability of existing work. New research can build on existing code and data focusing on addressing new novel questions, and avoiding reinvention of wheels and associated waste of time. Reproducible work can facilitate the generation of updates as new data become available. Reproducible open data products can also be used as communication and impact strategy expanding the original purpose of research findings (Nüst and Pebesma 2021). Reproducible code and data can be used to provide educational training and enable practitioners to address policy questions which were not outside the scope of the original research project (Rowe et al. 2020).
Calibration is at the centre of what makes spatial interaction models useful to researchers and practitioners. As (Openshaw 1975) describes it, “calibration is the process of providing estimates of the unknown parameters we have identified as the independent variables of the model.” In a basic gravity SIM formulation, we seek to estimate three parameters - as identified above - relating to origin mass, destination mass and a parameter determining the frictional effect of spatial separation between origins and destinations. These parameters reveal information about our system of interest - for example, how costly physical separation distances are to interaction.
Yet, we identified key challenges relating to the calibration of SIMs. Calibration requires both data and software. Forty or fifty years ago when many of the theoretical foundations of spatial interaction modelling were laid, the data landscape was somewhat different from today – spatial flow data were rarely available in volume and certainly not at the sort of temporal rhythm they are now where, for example, supermarket loyalty-card holders generate origin/destination revenue flow data from residential origins to store destinations at daily frequencies over time periods than can cover many years or even decades. As such, we might be forgiven for expecting that even if the science and theory underpinning the models has not developed very much, the software and processes facilitating calibration – relating empirical observations to the theoretical representations embodied in the models – might have. But in many ways, they have not. Today spatial flow data are ubiquitous. They can be derived from digital traces collected across various sensor networks involving mobile phones, social media, loyalty cards, smart card tickets and credit cards. Accessing interaction data is thus not the barrier it once was.
Yet, making sense of these data – understanding where commuting flows are unexpected, or differences in customer profiles shopping at similar retail stores – remains a challenge. Much of the challenge is because there is a dearth of knowledge within geographical education. Despite SIMs underpinning many social and geographical processes, these models are not taught to undergraduate geography students in the same way as, say, regression models are taught to economists or social psychologists. As such, it is not immediately obvious, even for those with geography degrees, how anyone might go about fitting their spatial flow data to a theoretical model, calibrating the parameters and revealing properties of their system. But, why have cohorts of undergraduate geography students not been taught how to fit these models and explore systems of spatial interaction?
Accessibility seems to represent an obstacle for the wider applicability
of SIMs. We discussed issues around reproducibility challenging the
practical application of SIMs, but that with packages like SPINT
(Oshan 2016) and our own efforts with the simodels package in R (see
Section 3.1, the tide is
beginning to turn. Yet, calibration remains a challenging sub-topic for
reproducibility and wider accessibility of these models, particularly
where algorithms which are able to calibrate parameters have remained
locked away - either behind dense algebraic notation in dusty papers
from the 1970s, or where they have found their way into commercial
software, behind paywalls.
Ironically, effective enough calibration routines have been available for as long as students have been running regression models in their introductory statistics classes. Occasional references can be found in the historic literature (e.g. (A. Stewart Fotheringham and Webber 1980); (Flowerdew and Aitkin 1982)) which lift the curtain and reveal that through reformulating the classic Wilsonian entropy maximising spatial interaction model as either a logged OLS regression model or a GLM utilising Poisson or negative binomial distributions, multiple parameters can be calibrated easily. These models are all available in common statistical software packages; but for most trying to make sense of the field coming across papers by some of the doyens (for it was and still is a male-dominated field) of the scene, practical expediency is often sacrificed at the alter of theoretical or technical prowess. And even then, while undoubtedly mathematically and theoretically rigorous, notes on calibration can be presented either as passing reference to ‘least squares’ or worse a lengthy derivation of maximum likelihood or Newton Raphson methods with no practical middle ground to assist novices in running a model.
As argued above, new technologies have enabled the emergence of ‘Big Data’ through the production and storage of large volumes of digital data. Much of these data contain location information and hence offer an opportunity to derive spatial flow data and understand spatial interactions between places. Big Data offer unique opportunities to study spatial interactions at unprecedented detailed geographical and temporal scales in real or near real-time across extensive populations and geographical areas. However, leveraging on these opportunities also involves major challenges for the analysis and modelling of spatial interactions (Rowe 2021). Furthermore, Big Data sources have often analysed ‘as-is’, without due attention paid to levels of validity and cross-comparison between data sources. Validation techniques and model/aggregate-data comparisons can help overcome these issues (Lovelace et al. 2016).
Limited research has focused on explicitly capturing patterns of non-stationarity in spatial interaction modelling despite the availability of suitable methods (Oshan 2021). While the issues of calibration discussed in Section 2.2 may have represented a barrier, lack of large enough data sets may have also hindered progress. Before the emergence of Big Data, the most common form of spatial flow data were cross-sections of origin-destination matrices derived from censuses or surveys, offering information at coarse geographical scales and population subgroups. The rise of data now offers more granular and denser volumes of data to capture patterns of spatial, temporal and population non-stationarity. The adoption and adaption of more sophisticated modelling frameworks will thus be required to effectively model these patterns.
Big Data also represent challenges for statistical inference. An standard practice in social sciences is to be guided by P values. Regression model estimates with P values below 0.05 threshold are commonly considered statistically significant and thus these estimates take central stage in most analyses. Modelling estimates derived from large data sets, however, often render P values below this threshold, calling for the adoption of alternative approaches. Such situation aligns with more general calls for a stop to the use of P values in the conventional, dichotomous way - to decide whether a result supports or refutes a scientific hypothesis. Additionally, Big Data offer an opportunity to embrace causal inference approaches. Reliance on cross-sectional data hindered the wide adoption of causal inference approaches to study the determinants of spatial interactions. Big Data now provides large, detailed longitudinal data sets to track spatial interactions and establish cause-and-effect relationships. Obtaining suitable time-varying data on relevant factors believed to shape the dynamics of spatial interactions may remain an obstacle. While data may be available, spatial integration of data may not be possible because of ethical considerations and data governance issues.
New methods are also required to handle, analyse and store large data sets. Traditional SIM frameworks were designed to identify significant relationships in small sample sizes with known properties. Big data are not collected for research purposes. They are an unintended consequence of administrative processes or social interactions and need to be reengineered for research. Handling Big Data requires a wider and new digital skills set, largely based on machine learning and artificial intelligence (ML/AI) and coding, in addition to greater knowledge of computing technology (e.g. Jupyter notebooks, Github and Docker) as well as scalability and parallelisation approaches. Except for a few centres, current university geography programmes and infrastructures are largely unprepared to deliver the required training. A multidisciplinary approach is needed to integrate computational training into human geography. ML/AI are likely to enhance prediction outcomes generated from SIMs. The idea of using ML/AI to model spatial interactions is not new, but the application has been limited due to the lack of large data sets. ML/AI are data hungry, requiring millions of data for effective training and validation. The rise of data provide an opportunity to promote the wider adoption of these models.
This section will describe the areas which should be developed to address the identified challenges.
Developing the essential infrastructure is key to enhance the
reproducibility and facilitate the calibration of SIMs. Software, open
science and digital technology (i.e. computational notebooks and Docker)
are important elements to develop an ecosystem that fosters reproducible
SIMs, provides adequate training and facilitate the application of SIMs.
We believe that an essential building block in this ecosystem is
user-friendly, efficient, open source software. Partly motivated by this
chapter, we have developed the simodels1 R package (Lovelace and
Nowosad 2022). 2 Below we present a reproducible example . simodels
enables the rapid develop of SIMs — starting from basic geographic
datasets as the key input — in comparatively few lines of code .
simodels does not just provide functions for running and fitting
(finding parameters to minimise model-observation differences). It
provides a framework for developing SIMs and creating new functions
implementing different types of SIM and using a variety of pre-existing
modelling tools in SIMs. We aim to expand the functionality of the
package building on the foundations presented below.
The first step to using the package and reproducing the minimal results shown below is to install R and an appropriate integrated development environment such as RStudio. After starting RStudio for the first time, you can get started with SIMs in a statistical programming environment that has strong support geographic visualisation (as we will see in the visualisations in this section) and modelling capabilities. The first step in this reproducible example is to install the package by entering and running the following command into the R console:
install.packages("simodels")We will also install tidyverse for intuitive data processing
functionality (Grolemund and Wickham 2016). Load the packages as
follows:
install.packages("tidyverse")library(simodels)
library(tidyverse)The starting ‘point’ is geographic entities representing trip start, end
(for ‘multi-partite’ models) or intermediate points. We use the word
‘features’ — meaning geographic vector entities (points, lines,
polygons) — with reference to the ‘simple features’ standard defined by
the Open Geospatial Consortium ((OGC) Open Geospatial Consortium Inc
2011). Almost all SIMs use points and polygons as the basis of origins
and destinations and raster datasets can be represented as simple
features. Such geographic features, and associated attributes (e.g. a
column named population representing the population of each
administrative zone) can be imported from standard spatial vector data
formats such as Shapefiles (.shp) GeoPackage (.gpkg) and GeoJSON
(.geojson) files with the sf package:
origin_zones = sf::read_sf("origin_zones.geojson")
destination_points = sf::read_sf("destination_points.geojson")The code chunk above imports two data objects:
-
A simple features object with ‘multipolygon’ geometries representing administrative zones that constitute trip origins (
origin_zones). -
A simple features object with ‘point’ geometries representing two popular pubs in Leeds as trip destinations (
destination_points).
Before creating SIMs representing travel to these two pubs in Leeds, we first perform some exploratory data analysis (EDA) to illustrate the input data (Beecham and Lovelace 2022):
origin_zones %>%
ggplot() +
geom_histogram(aes(x = to_pubs), binwidth = 10)
origin_zones %>%
ggplot() +
geom_sf(aes(fill = to_pubs), alpha = 0.5) +
geom_sf(data = destination_points)For many applications, the most important function in the simodels
package is si_to_od():
od_zones_to_points = si_to_od(origin_zones, destination_points)
class(od_zones_to_points)
nrow(od_zones_to_points)
names(od_zones_to_points)si_to_od() creates an ‘OD matrix’ represented in long form. As shown
in the output above, the result is a data frame with 94 rows,
representing the full combination of trips from each of the 47 origin
zones to each of the 2 destinations. The names in the data frame refer
to variables for origin and destination locations. When working on large
input data sets, the ‘full matrix’ of combinations can get unhelpfully
large: an OD dataset from every MSOA to every pub in England, for
example, would results in a data set with 350,000,000 (350 million)
rows. To reduce data set sizes, a ‘sparse matrix’ representing only OD
pairs below a certain distance threshold can be created by adding a
max_dist argument as shown below. The maximum Euclidean distance
between zone centroids and point destinations needs to be set, at 5 km
in this example. Note: si_to_od() calculates Euclidean between the
full combination of origins and destinations automatically.
od_zones_to_points = si_to_od(origin_zones,
destination_points,
max_dist = 5000)The resulting origin-destination data set is smaller (79 rows compared with 94 rows previously). While is not a major reduction, the process can greatly speed-up SIM processing, modelling and visualisation run times dealing with large data sets, tackling issues outlined in Section 2.3.
We can now specify a simple SIM model as follows:
gravity_model = function(beta, d, m, n) {
m * n * exp(-beta * d / 1000)
} and implement it with the following command:
od_to_pubs_result = od_zones_to_points %>%
si_calculate(fun = gravity_model,
m = origin_to_pubs,
n = destination_size,
d = distance_euclidean,
beta = 0.5,
constraint_production = origin_to_pubs)We can check the results:
sum(od_to_pubs_result$interaction)
#> [1] 2903
sum(origin_zones$to_pubs)
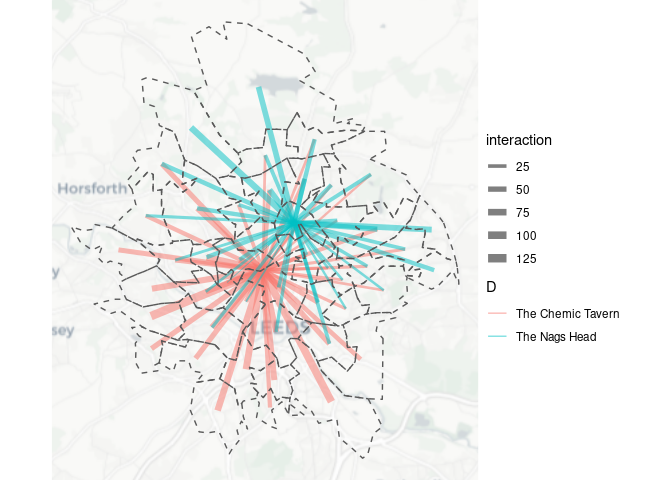
#> [1] 2903As shown above, the total number of trips is the same in the OD data as in the zone level data. We can visualise the result as follows, resulting in Figure ??:
library(ggspatial)
# rosm::osm.types()
od_to_pubs_result %>%
ggplot() +
annotation_map_tile(type = "cartolight") +
geom_sf(aes(lwd = interaction, colour = D), alpha = 0.5) +
scale_size_continuous(range = c(0.3, 3)) +
geom_sf(data = origin_zones, fill = NA, lty = 2, alpha = 0.5) +
theme_void()In the future we would like to see SIM development becoming as pain-free and intuitive as possible. We hope to see new open source SIM software projects being developed to reduce the ‘barrier to entry’ to SIMs. Building SIM software as part of popular languages for data science such as R, Python or Julia enables reproducibility, and access to a large ecosystem, as part of the SIM development process.
In terms of the simodels package briefly introduced in this section,
it is early days (the package was first published on CRAN in June 2022).
It has been tested on substantial input datasets and can certainly
enable SIMs to be developed, tested, and refined rapidly. In the future,
we would like to add pre-existing SIM models, for example a
si_gravity() function to provide a basic gravity model without having
to specify the functional form as we did above, to the package. Over
time, we would like to implement many such functions, perhaps a step
towards realising Alan Wilson’s vision of a ‘family’ of SIMs in open
source software (Wilson 1971). More broadly, the project is open source
and in that spirit of collaboration will evolve organically
(Franco-Bedoya et al. 2017); we encourage contributions and ideas on the
project’s issue tracker.3
We argue that research on SIMs should seek to adopt and adapt modelling frameworks to capture and understand patterns of spatial, temporal and population non-stationarity which can now be capture given the rise of large data sets. This line of enquiry involves calibrating models to estimate separate parameters for individual origins, destinations, time units and population segments. Such parameters can reflect local, temporal and population variations in the relationships producing spatial flows. Inference based on a set of global model parameters may lead to draw misleading conclusions due to misrepresentations of local-, temporal- and population-specific trends.
Yet, as noted above, limited progress has been made on capturing these patterns of non-stationarity (Oshan 2021). Existing approaches have been proposed to capture spatial-nonstationarity. An approach involves subsetting the overall data set into origin- or destination-specific data sets and calibrate individual models for each data set. An alternative approach is to include interaction terms between a binary categorical variable identifying an origin or destination, and each of the relevant covariates in a regression model. A third alternative is to use geographically weighted regressions (GWRs) to capture spatial non-stationarity (Graells-Garrido et al. 2021), but the extension of these models to calibrate spatial flow count data is challenging. It often requires the log transformation of spatial flows. Yet, such approaches may be inappropriate when dealing with sparse origin-destination matrices containing zeros. In such scenarios, using appropriate count distributions is recommended (O’Hara and Kotze 2010).
We propose generalised linear mixed models (GLMMs) as a more flexible modelling framework to capture all three sources of non-stationarity based on appropriate count data distributions. GLMMs extend GLMs to incorporate a combination of random and fixed effects parameters as predictor variables, and accommodate non-continuous responses, such as binary and count responses. Fixed effects represent a typical covariate and are typically used to capture “global” average patterns. Random effects are represented by categorical variables encoding some grouping unit, and can be used to estimate the extent of variations between and within groping units. Random effects are flexible, and in SIMs, units could comprise groups or individual origins, destinations, origin-destination pairs, time intervals or population subgroups to capture spatial, temporal and population variations in spatial flows. Unlike GWRs, the flexibility of GLMMs provides an opportunity selectively capture patterns of non-stationarity in relationships with a selected group of theoretically- or policy-relevant variables. In addition to flexibility, random effects can aid to correct statistical inference about fixed “global” effects by providing an estimation of variable in the response variables within and between groups. They can also reduce the probability of Type I error and Type I error (Harrison et al. 2018). GLMMs can also be used to explicitly model spatial and temporal auto-correlation.
Yet, challenges exist in applying GLMMs. First, GLMMs make additional assumptions about the data to those made in standard statistical approaches and they need to be tested
. Second, interpreting the model outputs from GLMMs correctly may be challenging, particularly estimates relating to variance components of random effects and correlations. Third, model selection is a challenge because of biases in model performance tests caused by the presence of random effects
. Guidelines for the implementation of GLMMs will therefore be needed to navegate these challenges and leverage the potential of these models to effectively account for non-stationarity in spatial flows.
We argue new ways of approaching statistical inference in SIMs. First, we call for a careful use of the concept of statistical significance. As highlighted in Section 2.3, dichotomising estimates into ‘statistically significant’ and ‘statistically non-significant’ is unhelpful and can lead to draw misleading conclusions, particularly for models relying on large data sets as the full set of estimates in such models can render P values below 0.05. An approach is embracing uncertainty, and re-conceptualing confidence intervals as ‘compatibility intervals’ can provide a practical solution (Amrhein, Greenland, and McShane 2019). This shifts the focus to all values inside the interval and to the fact that singling out a single point estimate may not be appropriate to draw broad conclusions about the factors underpining spatial flows.
Second, we argue for greater use of causal inferential approaches. Big Data now offers an unprecedented temporal frequency to capture spatial interactions in very short time frames, and understand the sequence of events to distinguish causes and consequences of these interactions. Identifying these causal-effect relationships is key to understand the impact of interventions and inform the development of policies aiming at generating a desired outcome. Inference statistical approaches are widely used in other social science disciplines, but these practices have not permeated through geography. Causal inference on spatial processes faces additional challenges, such as spatial dependence, spatial heterogeneity and spatial effects (Akbari, Winter, and Tomko 2021). So, while adopting causal inference methods to analyse spatial interactions may not be straightforward, we believe that is a valuable endeavor to inform the design of future policy interventions.
Third, we propose the use of multi-model inference. Intuitively,
multi-model inference seeks to draw conclusions from a range of
theoretically-sound model specifications (Burnham and Anderson 2004). It
uses model averaging to determine the direction and strength of
regression predictors, and enables the generation of Akaike Information
Criterion based weights from multiple models to assess the relative
importance of predictors in an outcome. As such, inferences are not
drawn from a single model, leading to more robust inferences, and offers
an alternative approach to evaluate the importance of predictors that
does not depend on statistical significance dicothomy. Additionally
determining the relevance of factors shaping spatial flows based on
multi-model inference offers an additional alternative to make inference
in the context of SIMs and Big Data. Multi-model inference has been
rarely applied to capture spatial interactions (Rowe 2013). Yet, it is
widely used in biology and ecology, and various routines exist in R
which can be integrated with simodels.
New methods and tools are needed to engineer and calibrate SIMs using large data sets. In agreement with Singleton and Arribas-Bel (2019), we recognise that the value of data science approaches to enable the calibration of SIMs on large data sets. We propose that data science can be beneficial on three key fronts. First, a key challenge is the storage, manipulation and analysis of large volumes of data. Large data sets cannot generally be stored and analysed on a computer’s local memory. Traditional approaches relying on local memory capacity to calibrate SIMs are therefore sub-optimal. Adoption of data science approaches to Big Data storage, scalability, high performance computing and parallel computing. Training and infrastructure to integrate these approaches are needed to enable researchers to unlock the opportunities afforded by Big Data, understanding spatial interactions in real-time or near real-time at more detailed temporal and spatial granularity.
Second, we propose the use of ML/AI to enhance the prediction capacity of SIMs. While this proposal is not new and ML/AI approaches have been deployed mainly in transport applications, their deployment in geography has been limited. Big Data now provides enough density of data to train and assess the capability of these algorithms to predict spatial interactions. Emerging evidence suggests that ML-calibrated SIMs outperform traditional GLM-calibrated SIMs at generated more accurate predictions of spatial interactions (Rowe, Mahony, and Tao 2022). ML/AI models do not require a pre-defined functional specification. They have the ability to uncover complex structure in the data and are rapidly deployable requiring limited human intervention. In the context of SIMs, the promise is that ML/AI can uncover and accommodate complex functional forms capturing patterns of spatial and temporal dependence and non-stationarity (Rowe, Mahony, and Tao 2022).
Third, ML/AI are also expected to enhance causal inference in SIMs. ML/AI-based methods are generally focused on prediction rather than understanding and establishing causal relationships. Yet, ML/AI models can be combined with causal inference to enhance the identification of cause-and-effect relationships. Many causal methods use prediction to generate instruments or counterfactuals in a first stage that can be employed in a second phase to produce “more” reliable estimates for statistical inference. Thus the fundamental problem of causal inference is the existence of a perfect analogue of out-of-sample performance for causal models, since counterfactual quantities are never observed. ML/AI models can be used to derive “better” counterfactuals and enhance inference on causality. At the same time, ML/AI can help scale causal effect estimation methods to SIMs based on high-dimensional data and unstructured data. ML/AI thus offers an opportunity to build accurate decision-support systems that estimate effect of interventions on spatial flows.
SIMs represent a core analytical tool to predict and understand spatial flows of people, information and products across our society and economy. Ultimately SIMs provide essential knowledge and information to support decision making and policy interventions. During the COVID-19 pandemic alone, SIMs have been essential generating critical evidence to monitor the geographical extent and speed of infection spread, retail, transport and movement activity by understanding human spatial interactions. Despite considerable progress over the past fifty years, we identified key challenges for the efficient deployment of SIMs in terms of reproducibility, calibration and Big Data modelling. We identified four areas of future development to tackle these challenges: (1) to enable essential infrastructure to facilitate the training, calibration and reproducibility of SIMs; (2) to embrace modelling frameworks to capture spatial, temporal and population heterogeneity; (3) to enhance statistical inference to accommodate Big Data analysis; and, (4) to integrate data science approaches to enhance SIM-generated predictions and statistical inference.
Akbari, Kamal, Stephan Winter, and Martin Tomko. 2021. “Spatial Causality: A Systematic Review on Spatial Causal Inference.” Geographical Analysis, December. https://doi.org/10.1111/gean.12312.
Amrhein, Valentin, Sander Greenland, and Blake McShane. 2019. “Scientists Rise up Against Statistical Significance.” Nature 567 (7748): 305–7. https://doi.org/10.1038/d41586-019-00857-9.
Arribas-Bel, Dani, Mark Green, Francisco Rowe, and Alex Singleton. 2021. “Open Data Products-A Framework for Creating Valuable Analysis Ready Data.” Journal of Geographical Systems 23 (4): 497–514. https://doi.org/10.1007/s10109-021-00363-5.
Beecham, Roger, and Robin Lovelace. 2022. “A Framework for Inserting Visually Supported Inferences into Geographical Analysis Workflow: Application to Road Safety Research.” Geographical Analysis n/a (n/a). https://doi.org/10.1111/gean.12338.
Brunsdon, Chris. 2016. “Quantitative Methods I.” Progress in Human Geography 40 (5): 687–96. https://doi.org/10.1177/0309132515599625.
Burnham, Kenneth P., and David R. Anderson, eds. 2004. Model Selection and Multimodel Inference. Springer New York. https://doi.org/10.1007/b97636.
Flowerdew, R., and M. Aitkin. 1982. “A Method of Fitting the Gravity Model Based on the Poisson Distribution.” Journal of Regional Science 22 (2): 191–202.
Fotheringham, A S. 1983. “A New Set of Spatial-Interaction Models: The Theory of Competing Destinations.” Environment and Planning A: Economy and Space 15 (1): 15–36. https://doi.org/10.1177/0308518x8301500103.
Fotheringham, A. Stewart, and M. J. Webber. 1980. “Spatial Structure and the Parameters of Spatial Interaction Models.” Geographical Analysis 12 (1): 33–46. https://doi.org/10.1111/j.1538-4632.1980.tb00016.x.
Franco-Bedoya, Oscar, David Ameller, Dolors Costal, and Xavier Franch. 2017. “Open Source Software Ecosystems: A Systematic Mapping.” Information and Software Technology 91: 160185.
Graells-Garrido, Eduardo, Feliu Serra-Burriel, Francisco Rowe, Fernando M. Cucchietti, and Patricio Reyes. 2021. “A City of Cities: Measuring How 15-Minutes Urban Accessibility Shapes Human Mobility in Barcelona.” Edited by Wenjia Zhang. PLOS ONE 16 (5): e0250080. https://doi.org/10.1371/journal.pone.0250080.
Grolemund, Garrett, and Hadley Wickham. 2016. R for Data Science. 1 edition. O’Reilly Media.
Harrison, Xavier A., Lynda Donaldson, Maria Eugenia Correa-Cano, Julian Evans, David N. Fisher, Cecily E. D. Goodwin, Beth S. Robinson, David J. Hodgson, and Richard Inger. 2018. “A Brief Introduction to Mixed Effects Modelling and Multi-Model Inference in Ecology.” PeerJ 6 (May): e4794. https://doi.org/10.7717/peerj.4794.
Hunt, Len M., Barry Boots, and Pavios S. Kanaroglou. 2004. “Spatial Choice Modelling: New Opportunities to Incorporate Space into Substitution Patterns.” Progress in Human Geography 28 (6): 746–66. https://doi.org/10.1191/0309132504ph517oa.
Lovelace, Robin, Mark Birkin, Philip Cross, and Martin Clarke. 2016. “From Big Noise to Big Data: Toward the Verification of Large Data Sets for Understanding Regional Retail Flows.” Geographical Analysis 48 (1): 59–81. https://doi.org/10.1111/gean.12081.
Lovelace, Robin, Nick Malleson, Kirk Harland, and Mark Birkin. 2014. “Geotagged Tweets to Inform a Spatial Interaction Model: A Case Study of Museums.” Arxiv Working Paper.
Lovelace, Robin, and Jakub Nowosad. 2022. “Simodels: Flexible Framework for Developing Spatial Interaction Models.” https://CRAN.R-project.org/package=simodels.
McFadden, D. 1974. Analysis of Qualitative Choice Behavior. Zarembka, p.(ed.): Frontiers in Econometrics. Academic Press. New York, NY.
Morgan, Malcolm, Marcus Young, Robin Lovelace, and Layik Hama. 2019. “OpenTripPlanner for R.” Journal of Open Source Software 4 (44): 1926. https://doi.org/10.21105/joss.01926.
Niedomysl, Thomas, Ola Hall, Maria Francisca Archila Bustos, and Ulf Ernstson. 2017. “Using Satellite Data on Nighttime Lights Intensity to Estimate Contemporary Human Migration Distances.” Annals of the American Association of Geographers 107 (3): 591–605. https://doi.org/10.1080/24694452.2016.1270191.
Nüst, Daniel, and Edzer Pebesma. 2021. “Practical Reproducibility in Geography and Geosciences.” Annals of the American Association of Geographers 111 (5): 1300–1310. https://doi.org/10.1080/24694452.2020.1806028.
O’Hara, Robert, and Johan Kotze. 2010. “Do Not Log-Transform Count Data.” Nature Precedings, January. https://doi.org/10.1038/npre.2010.4136.1.
(OGC) Open Geospatial Consortium Inc. 2011. “OpenGIS Implementation Specification for Geographic Information - Simple Feature Access - Part 1: Common Architecture.” https://www.ogc.org/standards/sfa.
Openshaw, Stan. 1975. Some Theoretical and Applied Aspects of Spatial Interaction Shopping Models. Vol. 4. CATMOG. Norwich: Geo Abstracts Ltd. https://github.com/qmrg/CATMOG/blob/Main/04-spatial-interaction-shopping.pdf.
Oshan, Taylor M. 2016. “A Primer for Working with the Spatial Interaction Modeling (SpInt) Module in the Python Spatial Analysis Library (PySAL).” REGION 3 (2): 11. https://doi.org/10.18335/region.v3i2.175.
———. 2021. “The Spatial Structure Debate in Spatial Interaction Modeling: 50 Years On.” Progress in Human Geography 45 (5): 925–50.
Pappalardo, Luca, Filippo Simini, Salvatore Rinzivillo, Dino Pedreschi, Fosca Giannotti, and Albert-László Barabási. 2015. “Returners and Explorers Dichotomy in Human Mobility.” Nature Communications 6 (1). https://doi.org/10.1038/ncomms9166.
Pereira, Rafael H. M., Marcus Saraiva, Daniel Herszenhut, Carlos Kaue Vieira Braga, and Matthew Wigginton Conway. 2021. “R5r: Rapid Realistic Routing on Multimodal Transport Networks with R5 in R.” Findings, March, 21262. https://doi.org/10.32866/001c.21262.
Popper, Karl. 1934. The Logic of Scientific Discovery. Hutchinson. http://books.google.com/books?id=MdvaSAAACAAJ&pgis=1.
Rowe, Francisco. 2013. “Spatial Labour Mobility in a Transition Economy: Migration and Commuting in Chile.” PhD thesis. https://doi.org/10.14264/uql.2017.427.
———. 2021. “Big Data and Human Geography.” http://dx.doi.org/10.31235/osf.io/phz3e.
Rowe, Francisco, Michael Mahony, and Sui Tao. 2022. “Assessing Machine Learning Algorithms for Near-Real Time Bus Ridership Prediction During Extreme Weather.” https://doi.org/10.48550/ARXIV.2204.09792.
Rowe, Francisco, Gunther Maier, Daniel Arribas-Bel, and Sergio Rey. 2020. “The Potential of Notebooks for Scientific Publication, Reproducibility and Dissemination.” REGION 7 (3): E1–5. https://doi.org/10.18335/region.v7i3.357.
Schwartz, Aba. 1973. “Interpreting the Effect of Distance on Migration.” Journal of Political Economy 81 (5): 1153–69.
Simini, Filippo, Marta C González, Amos Maritan, and Albert-László Barabási. 2012. “A Universal Model for Mobility and Migration Patterns.” Nature, February, 812. https://doi.org/10.1038/nature10856.
Singleton, Alex, and Daniel Arribas-Bel. 2019. “Geographic Data Science.” Geographical Analysis 53 (1): 61–75. https://doi.org/10.1111/gean.12194.
Wilson, AG. 1971. “A Family of Spatial Interaction Models, and Associated Developments.” Environment and Planning 3 (January): 132. https://doi.org/https://doi.org/10.1068/a030001.