방정식의 실근의 어림값 구하기
원리📚
곡선 y = f(x) 위의 적당한 점 (x1,f(x1))에서의 접선의 방정식은
y = f'(x1)(x - x1) + f(x1) 입니다.
y = f'(x1)x - f'(x1)x1 + f(x1) 이므로 y자리에 0을 넣고 정리하면
x = x1 - f(x1)/f'(x1) 입니다. 여기에서 x는 x절편이 됩니다.
위 x를 x2로 설정하고 이 과정을 반복하면 xn이 점점 방정식의 해에 가까워지게 됩니다.
그런데 만약 f'(xn)이 0이 나온다면 식을 계산할 수 없을 것입니다.
이를 방지하기 위해 기울기가 0이 나오면 - f(xn-1)/f'(xn-1)만큼 다시 이동시켜서 계산을 하도록 하였습니다.
(xn-1은 이전의 x의 위치)
만약 f'(x1)이 0이라면 x1값에 1을 더해주었습니다.
from sympy import *
%matplotlib inline
init_printing()def solve_equation(f, epoch = 10, t = 0, graph = False, xlim = (0,0), ylim = (0,0)) :
x = Symbol('x')
f_diff = diff(f, x)
move = 0
for i in range(epoch) :
if (f_diff.subs(x,t) == 0) :
if (move == 0) :
move += 1
t += move
continue
if (graph) :
line = expand(f_diff.subs(x,t)*(x-t) + f.subs(x,t))
plot(f,line, xlim=xlim, ylim=ylim)
move = - f.subs(x,t)/f_diff.subs(x,t)
t += move
if (f.subs(x,t) == 0) :
break
print(N(t))
print("근의 근사값은", N(t))
real = [N(m) for m in solve(f)]
print("실제 근은", real)실습🐥
이제는 여러가지 함수의 근의 근사값을 구해보고 파이썬 내장함수를 이용해서 구하는 실제 근과 비교해볼 것입니다.
실제 근에는 복소수도 포함되지만 근사값은 실수만 나오니까 참고해주세요!
다항함수 근 구하기
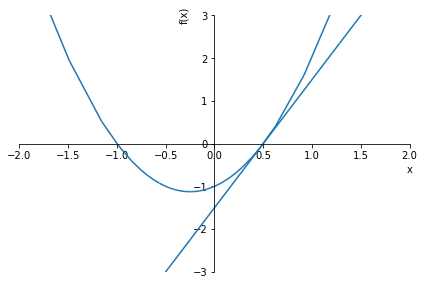
2x^2 + x -1 = 0
solve_equation(2*x**2 + x - 1)1.00000000000000
0.600000000000000
0.505882352941176
0.500022888532845
0.500000000349246
0.500000000000000
0.500000000000000
0.500000000000000
0.500000000000000
0.500000000000000
근의 근사값은 0.500000000000000
실제 근은 [-1.00000000000000, 0.500000000000000]
위 방정식은 실제로는 근이 두 개인데, 교과서 방법을 사용하면 처음 시작 위치에 따라 하나의 근밖에 구할 수 없습니다.
근을 모두 구하기 위해서는 초기 설정값을 다양하게 줘서 정확도를 높이는 방법을 사용할 수 있습니다.
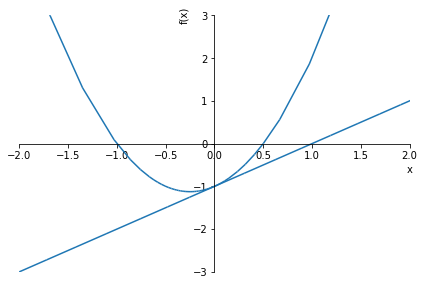
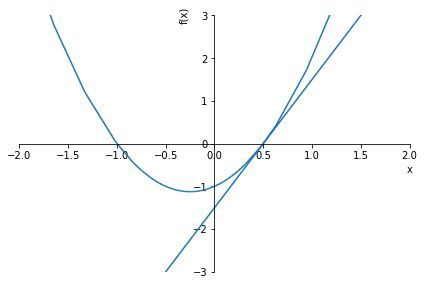
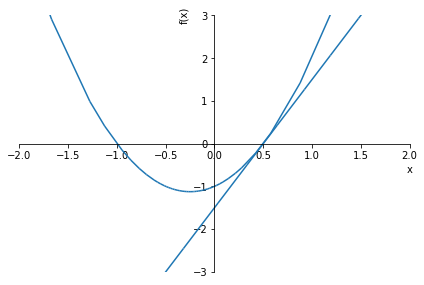
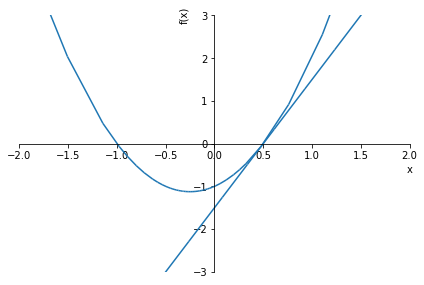
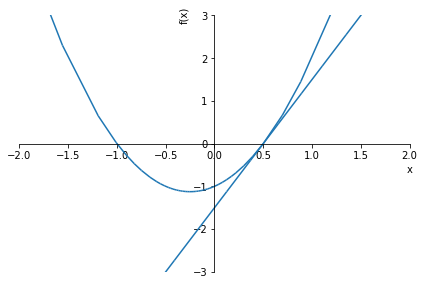
그래프로 알아보기📈
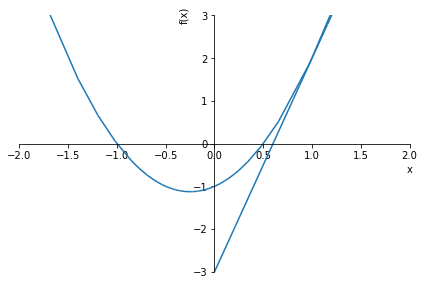
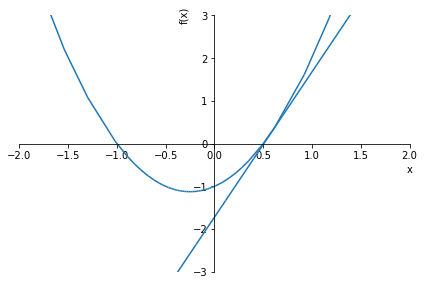
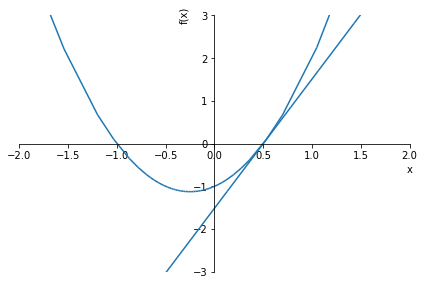
solve_equation(2*x**2 + x - 1, graph=True, xlim=(-2,2), ylim=(-3,3))1.00000000000000
0.600000000000000
0.505882352941176
0.500022888532845
0.500000000349246
0.500000000000000
0.500000000000000
0.500000000000000
0.500000000000000
0.500000000000000
근의 근사값은 0.500000000000000
실제 근은 [-1.00000000000000, 0.500000000000000]
초월함수 근 구하기
- e^x + x + 1 = 0
6번 이상 반복하면 시간이 너무 오래걸려 6번만 반복시켰습니다:)
solve_equation(exp(x) + x + 1, 6)-1.00000000000000
-1.26894142137000
-1.27845462385026
-1.27846454275036
-1.27846454276107
-1.27846454276107
근의 근사값은 -1.27846454276107
실제 근은 [-1.27846454276107]
- 1/x^2 + x + 1 = 0
이번에는 0에서 f(x)의 값이 존재하지 않는 함수입니다.
초기 x값을 0이 아닌 다른 값에 두면 해결할 수 있습니다.
혹시 몰라서 초기 x값을 양수, 음수로 다르게 설정해보았는데 같은 근사값이 나왔습니다.
solve_equation(1/x**2 + x + 1, t = 1)4.00000000000000
-1.22580645161290
-1.43661208869939
-1.46522775287122
-1.46557118494818
-1.46557123187677
-1.46557123187677
-1.46557123187677
-1.46557123187677
-1.46557123187677
근의 근사값은 -1.46557123187677
실제 근은 [0.232785615938384 + 0.792551992515448*I, 0.232785615938384 - 0.792551992515448*I, -1.46557123187677]
solve_equation(1/x**2 + x + 1, t = -1)-1.33333333333333
-1.45762711864407
-1.46554593270629
-1.46557123162226
-1.46557123187677
-1.46557123187677
-1.46557123187677
-1.46557123187677
-1.46557123187677
-1.46557123187677
근의 근사값은 -1.46557123187677
실제 근은 [0.232785615938384 + 0.792551992515448*I, 0.232785615938384 - 0.792551992515448*I, -1.46557123187677]
2^(1/4) 근 구하기(교과서)
solve_equation(x**4 - 2,t=2)1.56250000000000
1.30294700000000
1.20325256868678
1.18945113368314
1.18920719008396
1.18920711500273
1.18920711500272
1.18920711500272
1.18920711500272
1.18920711500272
근의 근사값은 1.18920711500272
실제 근은 [-1.18920711500272, 1.18920711500272, -1.18920711500272*I, 1.18920711500272*I]
교과서에 나오는 값과 같은 것을 확인할 수 있습니다!
활용 사례🤠
오늘 살펴본 방법처럼 함수의 그래프에서 기울기는 생각보다 다양한 것을 가능하게 해줍니다.
경사하강법
경사하강법: 기울기 반대쪽으로 계속 이동하여 함수의 최솟값을 찾는 방법
경사하강법을 이용한 모델 최적화는 인공지능과 데이터분석 분야의 기초 중의 기초라고 할 수 있습니다.
실제로 경사하강법은 선형회귀, 인공신경망 등 우리가 많이 들어본 모델들에서도 사용됩니다.
그러니까 미적분을 열심히 공부해야겠죠!ㅎㅎㅎ...