eschnett / DDF.jl

Discrete Differential Forms in arbitrary dimensions

Discrete Differential Forms

A Julia package for discretizing functions via finite elements.

• Documentation: Future documentation
• GitHub: Source code repository
• 
• 

Overview

The DDF package discretizes functions on arbitrary domains. The domain is decomposed into simplices, and the function is represented via a basis in each simplex. This is a form of a Finite Element discretization. For example, a scalar function in two dimensions might be represented via its values at the vertices. In between the vertices it might be defined via linear interpolation.

The DDF package is based on FEEC, the Finite Element Exterior Calculus. FEEC bears a certain similarity to DEC, the Discrete Exterior Calculus.

The design goals of the DDF package are:

• supports unstructured meshes (e.g. simplices)
• works in arbitrary dimensions
• supports higher order accurate discretizations
• is efficient enough for parallel/distributed calculations with large meshes with billions of elements
• is flexible and relatively easy to use so that it is useful for experimental mathematics

The DDF package is currently (2020-10-17) work in progress. Functionality is missing, and the current API is too tedious (too many details need to be specified explicitly).

Examples

Define a 2d manifold with Float64 coordinates that consists of a single simplex:

using DDF
D = 2
mfd = simplex_manifold(Val(D), Float64)
mfd = refined_manifold(mfd);
mfd = refined_manifold(mfd);

Calculate the gradient operator for the primal mesh:

grad = deriv(Val(Pr), Val(0), mfd)

Calculate the hodge dual operator for scalars on the primal mesh:

h = hodge(Val(Pr), Val(0), mfd)

Define a scalar function living on the primal vertices:

using DifferentialForms
f(x) = Form{D,0}((sin(x[1]) * cos(x[2]), ))
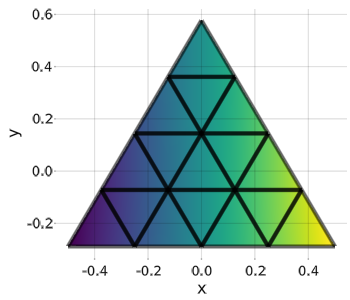
f̃ = sample(Fun{D,Pr,0,D,Float64,Float64}, f, mfd)

Plot the scalar function:

using AbstractPlotting
using GLMakie
using StaticArrays

coordinates = [mfd.coords[0][i][d] for i in 1:nsimplices(mfd, 0), d in 1:D]
connectivity = [SVector{D + 1}(i
                               for i in sparse_column_rows(mfd.simplices[D], j))
                for j in 1:size(mfd.simplices[D], 2)];
connectivity = [connectivity[i][n]
                for i in 1:nsimplices(mfd, D), n in 1:(D + 1)]
color = f̃.values;

scene = Scene()
poly!(scene, coordinates, connectivity, color=color, strokecolor=(:black, 0.6),
      strokewidth=4)
scale!(scene, 1, 1)

# using Makie
# Makie.save("simplex.png", scene; resolution=(350,300))

Literature and Related Work

• Douglas N. Arnold, Richard S. Falk, and Ragnar Winther, "Finite element exterior calculus, homological techniques, and applications", Acta numerica 15, 1-155 (2006), https://conservancy.umn.edu/bitstream/handle/11299/4216/2094.pdf.

• Douglas N. Arnold, Richard S. Falk, Ragnar Winther, "Finite element exterior calculus: from Hodge theory to numerical stability", arXiv:0906.4325 [math.NA].

• https://fenicsproject.org/documentation/.

• Anil N. Hirani, "Discrete Exterior Calculus", PhD thesis, http://www.cs.jhu.edu/~misha/Fall09/Hirani03.pdf.

• Nathan Bell, Anil N. Hirani, "PyDEC: Software and Algorithms for Discretization of Exterior Calculus", arXiv:1103.3076, https://github.com/hirani/pydec.

• Sharif Elcott, Peter Schröder, "Building your own DEC at home", https://doi.org/10.1145/1198555.1198667.